题目:

分析:
先不考虑天数的限制,直接对每一个人建一颗trie。
对于每一个人来说,他的x的贡献来源于trie树上所有在他右边的点(都比他大)。
将每一个子树所有的叶子结点记为f,x^2=(f1+f2+……fx)^2
将右式拆开看:f i *f i + f i * f j *2(枚举i,j统计贡献,*2是因为 i 和 j 可以交换)
再加上天数的限制:每一个人的A[i]异或上天数 j,相当于trie树的形态发生改变了(01边交换)
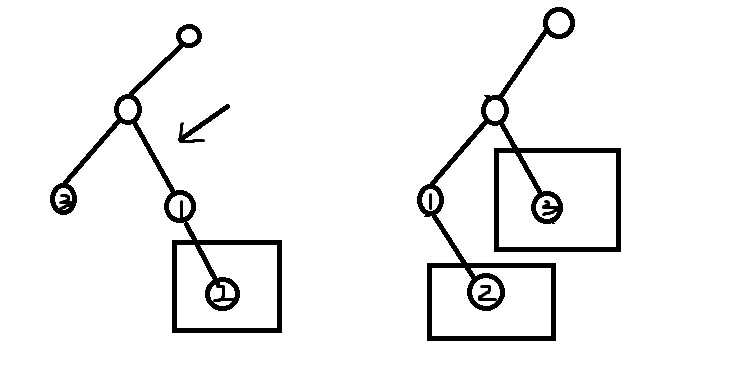
对于1来说,又多了一部分贡献,也就是说,对于右子树来说,当且仅当交换1条边会产生贡献,而其它的m-1条边随便交换,所以是f i * f i *(2^(m-1))
对于i,j来说,当两条边被交换了,才会产生贡献,所以是 f i * f j *2 *(2^(m-2))
dfs一遍trie树,统计答案即可。

#include<bits/stdc++.h> using namespace std; #define ll long long #define N 200005 #define ri register int const ll mod = 1e9+7; int go[N*30][2],siz[N*30],a[N],n,m,cnt=0; ll ans=0; void add(int x) { int now=0; for(ri i=m-1;i>=0;--i){ bool c=x&(1<<i); //这里的c一定要用bool,因为可能与出其它东西来,导致不是0和 1 if(!go[now][c]) go[now][c]=++cnt; now=go[now][c]; siz[now]++; } } void dfs(int x,ll sum,ll num)//num相当于是其它子树的siz { ll sz=siz[go[x][1]],tmp=0; tmp=sz*sz %mod *(1<<m-1) %mod; tmp=(tmp + sz*num %mod *(1<<m-1) %mod) %mod; if(go[x][0]) dfs(go[x][0],(sum+tmp) %mod, num+sz); sz=siz[go[x][0]],tmp=0; tmp=sz*sz %mod *(1<<m-1) %mod; tmp=(tmp + sz*num %mod *(1<<m-1) %mod) %mod; if(go[x][1]) dfs(go[x][1],(sum+tmp) %mod, num+sz); if(!go[x][0] && !go[x][1]) ans^=sum;//叶子节点 } int main() { freopen("race.in", "r", stdin); freopen("race.out", "w", stdout); scanf("%d%d",&n,&m); for(ri i=1;i<=n;++i) scanf("%d",&a[i]),add(a[i]); dfs(0,0,0); printf("%lld\n",ans); } /* 3 2 0 1 2 */



 浙公网安备 33010602011771号
浙公网安备 33010602011771号