T1:

很容易写出dp式子:定义dp[i][j]为现在是第i个烟火,位置在j,然后就可以枚举上一个时间的位置k转移过来。(j-(t[i]-t[i-1])*d <= k <=j+(t[i]-t[i-1])*d)
这样是n*n*m的,考虑优化。
固定一个边界:j-(t[i]-t[i-1])*d<=k
可以发现,当j变大,k的范围会变小,于是就可以维护一个单调递减的队列,队头就是答案。
而另外一个边界同理,只需要反过来做一遍就可以了。
注意:
1. 开滚动数组!!否则爆空间
2.不需要初始化负无穷,因为dp是直接从1开始更新的。

#include<bits/stdc++.h> using namespace std; #define N 305 #define M 150005 #define ll long long #define ri register int int m,a[N]; ll n,d,b[N],t[N],dp[2][M],q[M]; int read() { int x=0,fl=1; char ch=getchar(); while(ch<'0'||ch>'9') { if(x=='-') fl=-1; ch=getchar(); } while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar(); return x*fl; } int main() { freopen("fireworks.in", "r", stdin); freopen("fireworks.out", "w", stdout); n=read(); m=read(); d=read(); for(ri i=1;i<=m;++i) a[i]=read(),b[i]=read(),t[i]=read(); //for(ri i=0;i<=1;++i) for(ri j=0;j<=n;++j) dp[i][j]=-(1ll<<60); //for(ri i=1;i<=n;++i) dp[1][i]=b[1]-abs(i-a[1]); int now=0,pre=0; for(ri i=1;i<=m;++i){ pre=now,now^=1; //printf("%d %d\n",i,now); ll move=d*(t[i]-t[i-1]); if(move>n) move=n; int h=1,t=0; for(ri j=1;j<=n;++j){//正着考虑的是从j前面转移过来的 while(h<=t && q[h]+move<j) ++h; while(h<=t && dp[pre][j]>=dp[pre][q[t]]) --t; q[++t]=j; dp[now][j]=dp[pre][q[h]] + b[i]-abs(j-a[i]); } h=1,t=0; for(ri j=n;j>=1;--j){//反着考虑的是从j后面转移过来的 while(h<=t && q[h]-move>j) ++h; while(h<=t && dp[pre][j]>=dp[pre][q[t]]) --t; q[++t]=j; dp[now][j]=max(dp[now][j],dp[pre][q[h]] + b[i]-abs(j-a[i])); } } ll ans=-(1ll<<60); for(ri i=1;i<=n;++i) ans=max(ans,dp[now][i]); printf("%lld\n",ans); } /* 10 2 1 1 1000 4 9 1000 4 10 3 2 3 100 5 7 10 7 1 1 10 10 6 2 6 1 5 7 1 7 3 1 10 3 29 11 6 5 100 2 7 101 */
T2:

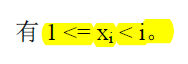
分析:
有依赖性的物品选择,就是树形背包。
如果成环,可以用tarjan缩点,如果是森林,可以连接超级源点。
这道题都不用,因为1<=xi<i,每个点向它前面的点连边,一定会成一棵树。
直接树形背包:
定义dp[i][j][0/1]为第i个节点,选了j的物品,子树中有没有用优惠券的最小花费。
但是这道题很坑的是,空间是256MB,直接开long long会爆空间,要针对题进行优化:
可见b最大只有1e9,dp大于b了,其实是没有用的,所以可以直接开int的dp数组,如果小于等于b就更新。
注意:
1.初始化要初始化全,要考虑到不选的情况。
2.当子树不用优惠券的时候,u这个根节点可以不选,不要漏了这种情况!!

#include<bits/stdc++.h> using namespace std; #define N 5005 #define ll long long #define ri register int ll c[N],d[N],b; int dp[N][N][2],n,tot=0,to[N],nex[N],head[N],siz[N]; void add(int a,int b) { to[++tot]=b; nex[tot]=head[a]; head[a]=tot; } void dfs(int u) { dp[u][1][0]=c[u]; dp[u][1][1]=c[u]-d[u]; dp[u][0][0]=0; siz[u]=1; for(ri i=head[u];i;i=nex[i]){ int v=to[i]; dfs(v); /*for(ri j=mid;j>=1;--j)//没有优化的是n^3 siz优化可达n^2 for(ri k=0;k<j;++k){ dp[u][j][0]=min(dp[u][j][0],dp[u][j-k][0]+dp[v][k][0]); dp[u][j][1]=min(dp[u][j][1],dp[u][j-k][1]+ min(dp[v][k][0],dp[v][k][1]) ); }*/ for(ri j=siz[u];j>=0;--j)//这里j必须取到0 因为可以由根不选转移 这时候根不使用优惠券 //j取0 为什么不会错呢? //考虑转移式子:tmp=dp[u][0][1] + (ll)min(dp[v][1][1],dp[v][1][0]) dp[u][0][1]是没有意义的 为正无穷 所以不会错 for(ri k=1;k<=siz[v];++k){ ll tmp=(ll) dp[u][j][0]+dp[v][k][0]; if(tmp<=b) dp[u][j+k][0]=min(dp[u][j+k][0],(int)tmp);// tmp=(ll) dp[u][j][1] + (ll)min(dp[v][k][1],dp[v][k][0]); dp[u][j+k][1]=min(dp[u][j+k][1],(int)tmp);// } siz[u]+=siz[v]; } } int main() { freopen("shopping.in","r",stdin); freopen("shopping.out","w",stdout); scanf("%d%lld",&n,&b); scanf("%lld%lld",&c[1],&d[1]); int fa; for(ri i=2;i<=n;++i) scanf("%lld%lld%d",&c[i],&d[i],&fa),add(fa,i); for(ri i=0;i<=n;++i) for(ri j=0;j<=n;++j) for(ri k=0;k<=1;++k) dp[i][j][k]=1e9+1; dfs(1); int ans=0; for(ri i=n;i>=0;--i){ if(dp[1][i][0] <= b || dp[1][i][1] <= b) { ans=i; break; } } printf("%d\n",ans); } /* 2 6 2 5 2 5 1 8 1000000000 400000000 300000000 800000000 300000000 1 200000000 100000000 1 400000000 200000000 2 700000000 200000000 2 300000000 200000000 2 700000000 300000000 5 200000000 100000000 3 8 11 4 3 8 3 1 2 1 1 4 2 2 7 2 2 3 2 2 7 3 5 2 1 3 */
T3:

分析:
考虑怎么统计方案数:当一个区间有x种删法,除开这个区间外有y种删法,那么总的合法删法=x*y(乘法原理)
我们可以将大区间化成许多小区间,转换成子问题,分别统计贡献。
如果递归到了一个右括号,那么无论怎么删都是不合法的,直接跳过。
如果递归到了一个左括号,就给它匹配一个右括号,去计算这一个区间的贡献。
最后到了单点,return 1(因为只有一个括号且它是合法的,1的方案来源于不删它)
最后记得减去1(题中要求)

#include<bits/stdc++.h> using namespace std; #define N 305 #define ll long long #define ri register int const int mod = 1e9+7; ll dp[N][N]; int n; char s[N]; ll dfs(int l,int r) { if(dp[l][r]!=-1) return dp[l][r]; if(l>=r) return 1; ll res=dfs(l+1,r); if(s[l]==']'||s[l]==')') return res; char tmp; if(s[l]=='(') tmp=')'; else tmp=']'; for(ri i=l+1;i<=r;++i) if(s[i]==tmp) { res=(res+ dfs(l+1,i-1) * dfs(i+1,r) ) %mod; }//break; return dp[l][r]=res; } int main() { freopen("parenthesis.in","r",stdin); freopen("parenthesis.out","w",stdout); scanf("%d",&n); scanf("%s",s); memset(dp,-1,sizeof(dp)); printf("%lld\n",dfs(0,n-1)-1);//不能打dp[0][n-1] 因为可能0位置是右括号 不合法 不能被更新到 } /* 21 ()[][]()[[]]][]()(()) 8 ()[][[]] */



 浙公网安备 33010602011771号
浙公网安备 33010602011771号