机房测试10：a 礼物分配（差分约束 or 贪心+线段树）

题目：

 

 

 

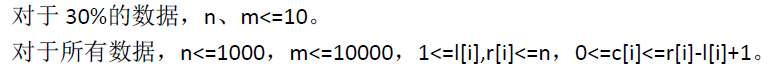
 分析：

法一： 差分约束

将题目中的限制写成三个不等式：（s数组是前缀和）

1.  s[r]-s[l-1]>=c

2.  s[r]-s[r-1]>=0

3.  s[r]-s[r-1]<=1

将第一个式子移项成最短路中dis的形式：s[r]>=s[l-1]+c

这个式子与：dis[i] >= dis[j]+c 相似，也就是说，j到i有一条c的边，j可以去更新i，所以将l-1连一条r的边。

下面两个式子也类似，但不是跑最短路，是跑最长路！！！

如果要跑最短路，就应该反着连负边。（画图模拟一下会发现）

下面的代码跑的是最短路，//划掉的是跑最长路的连边

最后spfa注意出队要标记置0！！

 

#include<bits/stdc++.h>
using namespace std;
#define ri register int
#define N 1005
#define M 100005
int read()
{
    int x=0,fl=1; char ch=getchar();
    while(ch<'0'||ch>'9') { if(ch=='-') fl=-1; ch=getchar(); }
    while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
    return x*fl;
}
int n,m,fl[N],dis[N],w[M],head[N],nex[M],to[M],tot=0;
int l[N],r[N],c[N],sum[N];
void add(int a,int b,int c) { to[++tot]=b; nex[tot]=head[a]; head[a]=tot; w[tot]=c; }
queue<int> q;
void spfa()
{
    //memset(dis,-10,sizeof(dis));
    //dis[0]=0; q.push(0); fl[0]=1;
    memset(dis,0x3f3f3f,sizeof(dis));
    dis[n]=0; q.push(n); fl[n]=1;
    while(!q.empty()){
        int u=q.front(); q.pop();
        fl[u]=0;
        for(ri i=head[u];i;i=nex[i]){
            int v=to[i];
            if(dis[v]>dis[u]+w[i]){
                dis[v]=dis[u]+w[i];
                if(!fl[v]) q.push(v);
            }
        }
    }
    printf("%d\n",-dis[0]);
}
int ans=1<<20;
void dfs(int now)
{
    if(now>n){
        bool fl=0;
        for(ri i=1;i<=n;++i) sum[i]=sum[i-1]+w[i];
        for(ri i=1;i<=m;++i) if(sum[r[i]]-sum[l[i]-1]<c[i]) { fl=1; break; }
        if(!fl) ans=min(ans,sum[n]);
        return ;
    }
    w[now]=0;
    dfs(now+1);
    w[now]=1;
    dfs(now+1);
}
void work1()
{
    for(ri i=1;i<=m;++i) l[i]=read(),r[i]=read(),c[i]=read();
    dfs(1);
    printf("%d\n",ans);
}
int main()
{
    freopen("a.in","r",stdin);
    freopen("a.out","w",stdout);
    n=read(); m=read(); 
    if(n<=10 && m<=10) { work1(); return 0; }
    int a,b,cc;
    for(ri i=1;i<=m;++i)
    a=read(),b=read(),cc=read(),add(b,a-1,-cc);//add(a-1,b,c)
    for(ri i=1;i<=n;++i)
    //add(i-1,i,0),add(i,i-1,-1);
    add(i,i-1,0),add(i-1,i,1);
    spfa();
    return 0;
}
/*
15 5
3 7 3
8 10 3
6 8 1
1 3 1
10 11 1

4 3
1 3 1
2 2 1
3 4 2
*/

 

法二：贪心+线段树

将区间排序（按左端点），每一次尽量贪心地将区间里面的元素往后放，（这样会使最后放的尽量少）。

在处理一个区间的时候，先看这个区间中已经有多少已经被选了，如果够了限制，就跳过，否则在区间末尾选够。

用线段树维护区间修改与区间查询。