机房测试10：车站分级 加强版（线段树优化建图+虚拟点）

题目：

 

 

 

弱化版

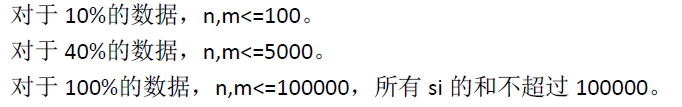
分析：

题目转化成，每次给出一段区间，在区间中选出几个点，选出的点比未选出的点等级高。

1. 将选出的点向区间中的每一个点都连权值为1的边，用拓扑求最长路径（一定是一个有向无环图），边数n*n*m，时间复杂度O（n*n*m）

2. 不直接连边，添加一个虚拟节点，将选出的点向虚拟节点连边，虚拟节点向区间连边，边数n*m，时间复杂度O（n*m）

3. 在2.的基础上，向区间中的每一个点连边改成用线段树向区间连边，边数m*logn，时间复杂度O（m*logn）

下面有两种连边方法：

1. 线段树中，父亲向儿子连边，权值为0。  叶子结点向虚拟节点连边，权值为1。  虚拟节点向区间连边，权值为0。

拓扑序中，入度为0的点是起点，出度为0的点是叶子节点，是终点。

最后跑出来是最高等级与最低等级的差，所以答案要+1

 

#include<bits/stdc++.h>
using namespace std;
#define N 200005
#define mid ((l+r)>>1)
#define ri register int
int read()
{
    int x=0,fl=1; char ch=getchar();
    while(ch<'0'||ch>'9') { if(ch=='-') fl=-1; ch=getchar(); }
    while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
    return x*fl;
}
int ndnum=4e5,tot=0,a[N],head[N<<2],to[N*20],nex[N*20],ru[N<<2],w[N*20];
int pos[N],dp[N<<2],n,m;
void add(int a,int b,int ww) {  to[++tot]=b; nex[tot]=head[a]; head[a]=tot; w[tot]=ww; ru[b]++;}
void build(int s,int l,int r)
{
    if(l==r) { pos[l]=s; return ; }
    add(s,s<<1,0); add(s,s<<1|1,0);
    build(s<<1,l,mid); build(s<<1|1,mid+1,r);
}
void add_q(int s,int l,int r,int L,int R,int id)
{
    if(L<=l && r<=R) { add(id,s,0); return ; }
    if(L<=mid) add_q(s<<1,l,mid,L,R,id);
    if(R>mid)  add_q(s<<1|1,mid+1,r,L,R,id);
}
queue<int> q;
void topu()
{
    memset(dp,-10,sizeof(dp));
    for(ri i=1;i<=ndnum;++i) if(!ru[i]) q.push(i),dp[i]=0;
    int ans=0;
    while(!q.empty()){
        int u=q.front(); q.pop();
        for(ri i=head[u];i;i=nex[i]){
            int v=to[i];
            dp[v]=max(dp[u]+w[i],dp[v]);
            ru[v]--;
            if(ru[v]==0) q.push(v); 
        }
    }
    for(ri i=1;i<=n;++i) ans=max(ans,dp[pos[i]]);//pos对应的叶子节点编号 
    printf("%d\n",ans+1);
}
int main()
{
    //freopen("c.in","r",stdin);
    //freopen("c.out","w",stdout);
    n=read(), m=read();
    build(1,1,n);
    for(ri i=1;i<=m;++i){
        int x=read();
        ++ndnum;
        for(ri j=1;j<=x;++j) a[j]=read();
        for(ri j=1;j<=x;++j) add(pos[a[j]],ndnum,1);
        for(ri j=2;j<=x;++j)//x!!!
        if(a[j-1]+1<=a[j]-1) add_q(1,1,n,a[j-1]+1,a[j]-1,ndnum); 
    }
    topu();
}
/*
5
5
2 2 4 
1 1 
1 3 
1 4 
3 1 2 4 

9 3
4 1 3 5 6
3 3 5 6
3 1 5 9
*/

 

 

 

2. 上面那一种连的边全部反着连，将叶子节点的初始点权值定为1，相当于最高等级，然后跑拓扑即可。

 

#include<bits/stdc++.h>
using namespace std;
#define N 200005
#define mid ((l+r)>>1)
#define ri register int
int read()
{
    int x=0,fl=1; char ch=getchar();
    while(ch<'0'||ch>'9') { if(ch=='-') fl=-1; ch=getchar(); }
    while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
    return x*fl;
}
int ndnum=4e5,tot=0,a[N],head[N<<2],to[N*20],nex[N*20],ru[N<<2],w[N*20];
int pos[N],flagg[N<<2],dp[N<<2],n,m; //printf("%d %d\n",a,b);
void add(int a,int b,int ww) {  to[++tot]=b; nex[tot]=head[a]; head[a]=tot; w[tot]=ww; ru[b]++;}
void build(int s,int l,int r)
{
    if(l==r) { pos[l]=s; flagg[s]=1; return ; }
    add(s<<1,s,0); add(s<<1|1,s,0);
    build(s<<1,l,mid); build(s<<1|1,mid+1,r);
}
void add_q(int s,int l,int r,int L,int R,int id)
{
    if(L<=l && r<=R) { add(s,id,0); return ; }
    if(L<=mid) add_q(s<<1,l,mid,L,R,id);
    if(R>mid)  add_q(s<<1|1,mid+1,r,L,R,id);
}
queue<int> q;
void topu()
{
    memset(dp,-10,sizeof(dp));
    for(ri i=1;i<=ndnum;++i) if(!ru[i]) q.push(i),dp[i]=flagg[i];//叶子节点初始化为1 
    int ans=0;
    while(!q.empty()){
        int u=q.front(); q.pop();
        for(ri i=head[u];i;i=nex[i]){
            int v=to[i];
            dp[v]=max(dp[u]+w[i],dp[v]);
            ru[v]--;
            if(ru[v]==0) q.push(v); 
        }
    }
    for(ri i=1;i<=n;++i) ans=max(ans,dp[pos[i]]);//pos
    printf("%d\n",ans);
}
int main()
{
    freopen("c.in","r",stdin);
    freopen("c.out","w",stdout);
    n=read(), m=read();
    build(1,1,n);
    for(ri i=1;i<=m;++i){
        int x=read();
        ++ndnum;
        for(ri j=1;j<=x;++j) a[j]=read();
        for(ri j=1;j<=x;++j) add(ndnum,pos[a[j]],1);
        for(ri j=2;j<=x;++j)//x!!!
        if(a[j-1]+1<=a[j]-1) add_q(1,1,n,a[j-1]+1,a[j]-1,ndnum); 
    }
    topu();
}
/*
5
5
2 2 4 
1 1 
1 3 
1 4 
3 1 2 4 

9 3
4 1 3 5 6
3 3 5 6
3 1 5 9
*/