题目:

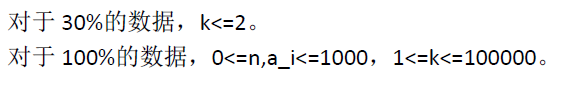
分析:
先手推一个显然的式子: a*x+b*y+c*z……=( x+y+z+…… )*n
将右边移项到左边,可以得到:a*(x-n)+b*(y-n)+c*(z-n)……=0
现在转化成求合法且最小的x,y,z。
假设现在在0号节点,买一杯鸡尾酒就相当于跳一截,问题转换成了最少跳多少次能够回到0号节点。
把跳一次的贡献算成1,用bfs求一遍就好了。
但时间复杂度会很高,因为有很多状态被重复遍历。
直接用vis打标记即可。因为n是小于1000的,所以点集是0~2000(有负数存在)
最后复杂度:n^2(每个点会被遍历一次,每一次会枚举遍历哪个点)

#include<bits/stdc++.h> using namespace std; #define ri register int #define N 100005 int read() { int x=0,fl=1; char ch=getchar(); while(ch<'0'||ch>'9') { if(ch=='-') fl=-1; ch=getchar(); } while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar(); return x*fl; } int a[N],dp[N],vis[N]; queue<int> q; int main() { freopen("d.in","r",stdin); freopen("d.out","w",stdout); int x=read(), k=read(); for(ri i=1;i<=k;++i){ a[i]=read(),a[i]-=x; if(a[i]==0) { printf("1\n"); return 0; } } sort(a+1,a+1+k); int num=unique(a+1,a+1+k)-a-1;//一定要去重 否则点集就会是100000 if(a[1]>0||a[num]<0) { printf("-1\n"); return 0; } memset(dp,0x3f3f3f,sizeof(dp)); q.push(1000); dp[1000]=0; while(!q.empty()){ int u=q.front(); q.pop(); for(ri i=1;i<=num;++i){ if( a[i]+u>=0 && a[i]+u<=2000 && (!vis[a[i]+u]) ) dp[a[i]+u]=dp[u]+1,q.push(a[i]+u),vis[a[i]+u]=1; } } printf("%d\n",dp[1000]); return 0; } /* 13 5 3 5 3 5 3 12 2 3 19 50 2 100 25 */



