题目:

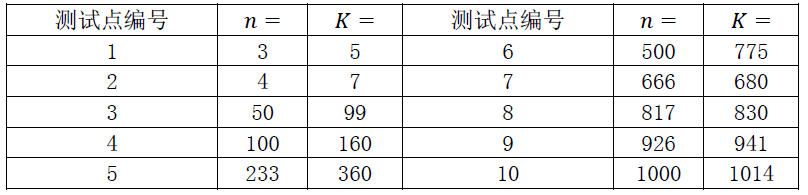
分析:
其实我们可以不用管k的大小,我们只需构造一组合法的,使得元素个数最小(一定会小于等于k)
可以看做一个从只有一个1,跳跃到n个1的过程,模拟一下,感受如何跳跃才是最快的:
1:00000001
2:00000010
(1+2)
3:00000011
(……)
4:00001100
(3+4)
5:00001111
(……)
6:1111 1111
也就是说:遇到偶数,就左移它有的1的个数那么多位(将1的个数翻倍,倍增思想),遇到奇数,就将上两个数求和,变成最后几位是连续的1的状态。
可以证明,这样一定是最快的,对于n不为2的次幂时,特殊处理一下到哪一位停止。
再手推一下公式得到初始的k值。

#include<bits/stdc++.h> using namespace std; #define ri register int #define N 2005 int x[N][2*N],n,k,fl; int read() { int x=0,fl=1; char ch=getchar(); while(ch<'0'||ch>'9') { if(ch=='-') fl=-1; ch=getchar(); } while(ch<='9'&&ch>='0') x=x*10+ch-'0',ch=getchar(); return x*fl; } void print(int a,int cnt) { for(ri i=1;i<=cnt+1;++i){ for(ri j=i;j<=n+i-1;++j) printf("%d",x[a][j]); printf("\n"); if(x[a][i]) { fl=1; return ; } } } int main() { freopen("exam.in","r",stdin); freopen("exam.out","w",stdout); n=read(); k=read(); int ans=0; for(ri i=1;i<=n;++i) if((1<<i)>n) { ans=i-1; break; } if(n==(1<<ans)) printf("%d\n",(1<<ans)+ans); else printf("%d\n",ans+1+n); x[1][n]=1; int now=1,i=2; while(!fl){ if(i&1){ for(ri j=1;j<=n;++j) x[i][j]=x[i-1][j]+x[i-2][j]; now*=2; } else{ for(ri j=1;j<=n;++j) x[i][j]=x[i-1][j+now]; print(i-1,now); } i++; } for(ri i=1;i<=n;++i) printf("1"); return 0; } /* 3 5 */




 浙公网安备 33010602011771号
浙公网安备 33010602011771号