机房测试7：paint（分治+st表）

题目：

 

 

 

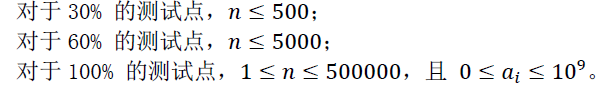
 分析：

与noip2018 T1十分相似，那道题可以看做这道题只能横着涂，具体思路是：

第一次先选取最小的高度minn，让所有高度都减去minn，1~n的连续段就被分成了许多块，对于每一个块重复上述过程，直到所有的柱子都为0。

这种过程类似于递归处理块，可以用dfs解决。

对于区间l~r，在这道题中，我们可以横着选，也可以花费r-l+1，选择竖着选，只需要在递归的时候比较一下答案即可。

但每次找最小值及其位置的时候，用st表维护最小值及其位置，可以将n^2化为n*logn

#include<bits/stdc++.h>
using namespace std;
#define ri register int
#define ll long long
#define N 500005
int n,low[N],a[N];
ll read()
{
    ll x=0,fl=1; char ch=getchar();
    while(ch<'0'||ch>'9') { if(ch=='-') fl=-1; ch=getchar(); }
    while(ch<='9'&&ch>='0') x=x*10+ch-'0',ch=getchar();
    return x*fl;
}
struct st { 
    int w; int pos;//开long long会爆空间 
    inline bool friend operator<(const st x,const st y){
        return x.w<y.w;
    }
}mn[N][22];
st calc(int l,int r)
{
    int k=low[r-l+1];
    return min(mn[l][k],mn[r-(1<<k)+1][k]);
}
ll dfs(int l,int r,int h)
{
    if(l>r || r<0) return 0;
    //if(l==r) return 1;
    st minn=calc(l,r);
    ll ans=minn.w-h;
    ans+=dfs(l,minn.pos-1,minn.w);//递归处理块 
    ans+=dfs(minn.pos+1,r,minn.w);
    return min((ll)r-l+1,ans);//考虑竖着涂会不会更优 
}
int main()
{
    freopen("paint.in","r",stdin);
    freopen("paint.out","w",stdout);
    n=read();
    for(ri i=1;i<=n;++i) a[i]=read();
    low[0]=-1;
    for(ri i=1;i<=n;++i) low[i]=low[i/2]+1;
    for(ri i=1;i<=n;++i) mn[i][0].w=a[i],mn[i][0].pos=i;
    for(ri j=1;j<=20;++j)
     for(ri i=1;i+(1<<j)-1<=n;++i)
      mn[i][j]=min(mn[i][j-1],mn[i+(1<<(j-1))][j-1]);
    printf("%lld\n",dfs(1,n,0));
}
/*
5
2 2 1 2 1
*/