题目:

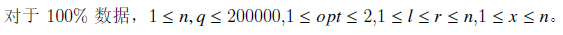
分析:
暴力:记录每个集合的每个元素,暴力区间修改,区间求和。
这个题很容易想到线段树,难点在于如何快速地确定一个集合是否出现过某个元素。
考虑维护两个线段树:
一个是答案线段树,维护区间元素个数和。(乘加标记的普通线段树)
一个是判断一段区间是否都有某个元素(动态开点线段树):
1.在modify的时候如果都有,就直接将这段区间的答案加倍(在答案线段树里面更新)
2.如果都没有就在这段区间里面加入这个元素,同时这段区间的答案增加。
3.如果一部分区间有,一部分没有,就递归子区间,直到答案以上两种状态为止。
如何维护第二个线段树?
每一次插入一个数的时候,对它新建一个点(如果之前没有这个点),w数组表示这种元素对应的某个区间里有多少个集合有这种元素。
比如说元素为3,令x为这个元素对应的2~5区间的下标值,若2~5这个区间有2、3这两个集合有这个元素,那么w[x]=2。
如果对每一个元素都维护它对应的每一个区间,那么空间应该是n*n*logn的。
但是我们会发现,有很多区间都是没有用到的(因为最多只会modify 2*10^5次),所以可以动态开点。
空间复杂度:n*logn(每次修改一个区间 ,最多递归log层, 最多开log个新点, 最多有n次操作)
注意:
乘加标记的下放为什么是先下放乘标记,再下放加标记?
1.先乘后加:明显应该先下放乘标记。
2.先加后乘:看起来好像 (a+b)*c -> (a*c)+b 是不对的,但其实在打区间乘标记递归到一个完整区间的时候,有一个这样的操作:
add[s] = add[s]*v %mod; 也就是说上面的b已经不是原来的b了,而是b*c,由乘法分配律可知上式是对的。
下放标记的时候记得把加标记也乘上乘标记!!

#include<bits/stdc++.h> using namespace std; #define ri register int #define mod 998244353 #define mid ((l+r)>>1) #define N 200005 #define ll long long ll sum[N*4],mul[N*4],add[N*4]; int cnt=0,n; int read() { int x=0,fl=1; char ch=getchar(); while(ch<'0'||ch>'9') { if(ch=='-') fl=-1; ch=getchar(); } while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar(); return x*fl; } void update_sum(int s) { sum[s]=(sum[s<<1]+sum[s<<1|1]) %mod; } void build(int s,int l,int r) { add[s]=0; mul[s]=1; if(l==r) { sum[s]=0; return ; } build(s<<1,l,mid); build(s<<1|1,mid+1,r); update_sum(s); } void pushdown1(int s,int l,int r) { mul[s<<1]=mul[s<<1]*mul[s] %mod; mul[s<<1|1]=mul[s<<1|1]*mul[s] %mod; add[s<<1]=add[s<<1]*mul[s] %mod; add[s<<1|1]=add[s<<1|1]*mul[s] %mod; add[s<<1]=(add[s<<1]+add[s]) %mod; add[s<<1|1]=(add[s<<1|1]+add[s]) %mod; sum[s<<1]=sum[s<<1]*mul[s] %mod; sum[s<<1|1]=sum[s<<1|1]*mul[s] %mod; sum[s<<1]=(sum[s<<1]+add[s]*l) %mod; sum[s<<1|1]=(sum[s<<1|1]+add[s]*r) %mod; add[s]=0; mul[s]=1; } void modify_add(int s,int l,int r,int L,int R) { if(L<=l && r<=R) { sum[s]=(sum[s]+r-l+1)%mod; add[s]=(add[s]+1)%mod; return ; } if(mul[s]!=1 || add[s]) pushdown1(s,mid-l+1,r-mid); if(L<=mid) modify_add(s<<1,l,mid,L,R); if(R>mid) modify_add(s<<1|1,mid+1,r,L,R); update_sum(s); } void modify_mul(int s,int l,int r,int L,int R) { if(L<=l && r<=R) { sum[s]=sum[s]*2%mod; add[s]=add[s]*2%mod; mul[s]=mul[s]*2%mod; return ; } if(mul[s]!=1 || add[s]) pushdown1(s,mid-l+1,r-mid); if(L<=mid) modify_mul(s<<1,l,mid,L,R); if(R>mid) modify_mul(s<<1|1,mid+1,r,L,R); update_sum(s); } ll query(int s,int l,int r,int L,int R) { if(L<=l && r<=R) return sum[s]; pushdown1(s,mid-l+1,r-mid); ll ans=0; if(L<=mid) ans+=query(s<<1,l,mid,L,R); if(R>mid) ans+=query(s<<1|1,mid+1,r,L,R); return ans%mod; } int rt[N],ch[N*30][3];//每次修改一个区间 最多递归log层 最多开log个新点 最多有n次操作 所以开nlogn的数组!! ll w[N*30],mark[N*30]; void pushdown2(int s,int l,int r) { if(!mark[s]) return ; if(!ch[s][0]) ch[s][0]=++cnt; if(!ch[s][1]) ch[s][1]=++cnt; mark[ch[s][0]]=1; mark[ch[s][1]]=1; w[ch[s][0]]+=l; w[ch[s][1]]+=r; mark[s]=0; } void update_w(int s) { w[s]=w[ch[s][0]]+w[ch[s][1]]; } void modify(int &p,int l,int r,int L,int R) { if(!p) p=++cnt; if(L==l && r==R){ if(w[p]==r-l+1){ modify_mul(1,1,n,l,r);//*2 } else if(!w[p]){ mark[p]=1; w[p]=r-l+1; modify_add(1,1,n,l,r);//+1 } else{ pushdown2(p,mid-l+1,r-mid); modify(ch[p][0],l,mid,L,mid); modify(ch[p][1],mid+1,r,mid+1,R); update_w(p); } return ; } pushdown2(p,mid-l+1,r-mid); if(R<=mid) modify(ch[p][0],l,mid,L,R); else if(L>mid) modify(ch[p][1],mid+1,r,L,R); else modify(ch[p][0],l,mid,L,mid),modify(ch[p][1],mid+1,r,mid+1,R); update_w(p); } int main() { freopen("multiset.in","r",stdin); freopen("multiset.out","w",stdout); n=read(); int q=read(); build(1,1,n); while(q--){ int op=read(),x=read(),y=read(); if(op==1){ int v=read(); modify(rt[v],1,n,x,y); } else { printf("%lld\n",query(1,1,n,x,y)); } } return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号