题目:

(鉴于题意描述过于糊,将这道题变成了一道阅读理解题,下面自己描述一遍题意)
求一个位置,从那个位置出发向上下左右同时流,遇到B可以流,其它不能流,流出给出数据的样子。
例如一个不合法的位置是2,5 。因为从它出发要流过上下左右的点,而给出的图中它的上下都是B,则说明没有被流过。
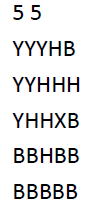
ans=2 3
分析:
暴力:枚举每一个点是否能作为起点,bfs检查(不能用dfs!!)
非正解但可以过:像刚刚给出的2,5这种点,它旁边是B,则说明它一定是最后一个流过的点,反推与它相邻的点,是倒数第二流过的点,一直向回推,直到推到起点。
这种过程明显可以用bfs实现,用一个队列去存储每一个点是第几个被递推到。
问题是这样推可能会推到多个起点,就把这些点存下来,再去bfs检查。(相当于一个剪枝,剪掉了许多不可能成为起点的点)
如何检查:
如果一个点旁边又有H又有B则不合法。

#include<bits/stdc++.h> using namespace std; #define N 305 #define nn N*N int dx[5]={0,0,1,-1},dy[5]={1,-1,0,0},x[nn],y[nn],id[N][N],h[N][N]; bool vis[N][N],fl=false; char s[N],a[N][N]; bool bfs(int now) { queue<int> qu; memset(vis,false,sizeof(vis)); qu.push(now); while(!qu.empty()){ int u=qu.front(); qu.pop(); bool fl1=false,fl2=false; for(int i=0;i<=3;++i){ int xx=x[u]+dx[i],yy=y[u]+dy[i]; if(vis[xx][yy]) continue; if(a[xx][yy]=='H'){ vis[xx][yy]=true; qu.push(id[xx][yy]); fl1=true; } if(a[xx][yy]=='B') fl2=true; if(fl1&&fl2) return false; } } return true; } queue<int> q; int main() { freopen("calm.in","r",stdin); freopen("calm.out","w",stdout); int n,m,num=0,maxn=0,ans=0; scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) id[i][j]=++num,x[num]=i,y[num]=j; for(int i=1;i<=n;++i){ scanf("%s",s); for(int j=1;j<=m;j++){ a[i][j]=s[j-1]; if(s[j-1]=='B') q.push(id[i][j]); } } while(!q.empty()){ int now=q.front(); q.pop(); for(int i=0;i<=3;++i){ int xx=x[now]+dx[i],yy=y[now]+dy[i]; if(a[xx][yy]=='H' && !vis[xx][yy]){ q.push(id[xx][yy]); vis[xx][yy]=true; h[xx][yy]=h[x[now]][y[now]]+1; maxn=max(maxn,h[xx][yy]); } } } for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if(h[i][j]==maxn) q.push(id[i][j]); while(!q.empty()){ int now=q.front(); q.pop(); if(bfs(now)) { ans=now; break; } } if(ans) printf("%d %d\n",x[ans],y[ans]); else printf("-1\n"); return 0; } /* 5 5 YYYHB YYHHH YHHXB BBHBB BBBBB 10 10 12345678910 1 YYBBBBBBXX 2 YYBBBBBBBB 3 XXBBBBBHBB 4 BXXBBBHHHB 5 BBXBBHHHHH 6 BBBXXHXHHH 7 BBBXXHHHHH 8 BBBBXXHHXH 9 XBBBXXXHXX 10XXBBBBHHXX h: 0000000000 0000000000 0000000100 0000001210 0000012321 0000020432 0000034543 0000005404 0000000300 0000001200 */




 浙公网安备 33010602011771号
浙公网安备 33010602011771号