首先看看大佬的博客
下面是推理过程,然而我们只需要记结论(h,g,f 都是假定的函数,S是f的前缀和函数):
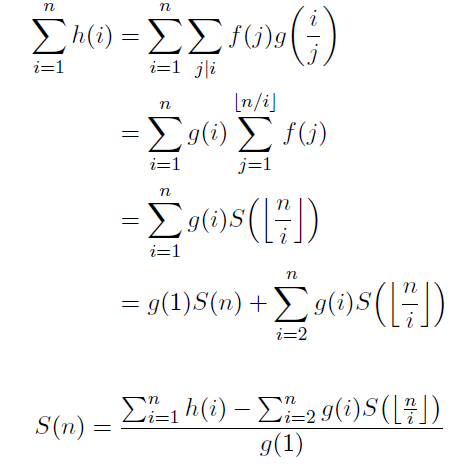
例题1:N=1e10 ,求下式
思路:S(i)是f的前缀和,我们想找到一个g使得h的前缀和好求(h=f*g)。
先将h的式子写出来:![]()
再把f套成u,我们会发现,前面那一部分是可以套莫比乌斯的性质的:![]()
那么把g带成1函数,f*g就等于元函数,而元函数的前缀和不就是1吗?
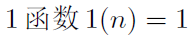
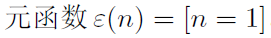
然后我们就可以快乐地将化简后的h带入S(n)(也是要求的M(n))那个式子中:![]()
最后复杂度是N的2/3次方(我也不知道为啥)
明显对于后半部分可以用整除分块来求,注意代码实现:(sum是f函数的前缀和)
int dfs(ll x) { if(x<=N-5) return sum[x]; if(mp[x]) return mp[x];//用map来记录是否已经计算过 ll ans=1; for(ll l=2,r;l>=0&&l<=x;l=r+1){//循环从2开始 r=x/(x/l);//*(r-l+1)是因为这个数重复了这么多次 ll xx=*(r-l+1)*dfs(x/l); ans=(ans-xx+mod)%mod;//注意要防止ans加成负数!! +mod %mod } return mp[x]=ans; }
例题2:N=1e10,求:![]()
和上面一样,我们先写出h(n): ,再把f当做:
,再把f当做: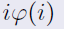 代入。
代入。
然后我们惊奇地发现,前面一部分不是可以用欧拉函数的性质替换吗?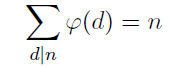
现在只剩下了 d*g( n/d ),那g取什么呢?明显取id函数又可以快乐地把d抵消掉了! 最后h(n)=n^2。 (id函数:单位函数,id(n)=n)
ans的初始值是什么呢?前x的平方和式子是:n*(n+1)*(2n+1)/6。代码实现就仿照刚刚那个啦。
例题3:N=1e10,求![]()
和上面的一样,自己动手推一下
好了经过一番推理之后,g也是同上题一样,也是取id函数的,下面是代码:
int dfs(ll x) { if(x<=N-5) return sum[x]; if(mp[x]) return mp[x]; ll ans=1; for(ll l=2,r;l>=0&&l<=x;l=r+1){ r=x/(x/l);//*(r-l+1)是因为这个数重复了这么多次 ll xx=(l+r) %mod *inv2 %mod *(r-l+1) %mod *dfs(x/l) %mod;//注意要对2求逆元 //L+r/2是因为原式里面有i 所以跳过一个区间时要加上这个区间和 :(l+r)/2首项加末项除以二 ans=(ans-xx+mod)%mod; } return mp[x]=ans; }
然后是一个式子化简的小技巧: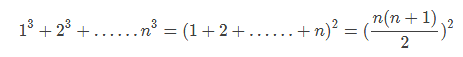
最后说说N的范围,N太小了会T,太大了也可能会T,最好取600万
可以写写的题:洛谷P4213,P3768
完结啦~~


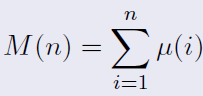
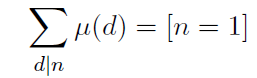
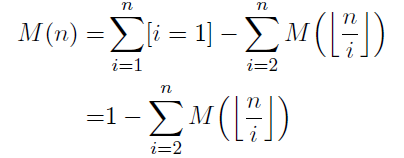
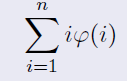
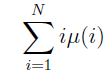

 浙公网安备 33010602011771号
浙公网安备 33010602011771号