读文献--综述Comparison and evaluation of pathway-level aggregation methods of gene expression data

读文献--综述:Comparison and evaluation of pathway-leel aggregation methods of gene expression data

Introduction

Background

得到数据的功能性的理解集中于基因集的功能,比如pathways而不是单个基因.现在pathway-level的分析主要是ORA和GSEA,另外的方法也在探索.该方法首先在pathway层面整合基因表达数据，将原始数据转化为每一行对应一个pathway而不是一个基因的紧凑表示。然后，利用现有的基因表达数据算法，将pathway表达数据用于pathway空间的差异表达和分类分析。虽然有几项研究提出了pathway-level整合方法，但由于评估的范围有限，因此尚不清楚它们如何相互比较。因此，本研究对6种最突出的整合方法进行了综合评价。

Results

现在主要比较五种方法,分别是:

1. mean of all member genes (Mean all)
2. mean of condition-responsive genes (Mean CORGs)
3. analysis of sample set enrichment scores (ASSESS)
4. principal component analysis (PCA), and partial least squares (PLS)
5. a variant of an existing method (Mean top 50%, averaging top half of member genes).

测试数据是:

​ 通过收集包括各种表型的7对相关但独立的数据集，进行全面和严格的基准测试。

测试结果:

在KEGGpathway的空间内进行整合。通过对内部和外部的分类准确性及检查数据集对之间pathway特征的相关程度来评估方法的性能。评估结果显示:(i) 'ASSESS'和'Mean top 50%'获得了最好的准确性和相关性，(ii)均值都显示出最低的准确性，(iii)平均CORGs和PLS在pathway特征相关性中引起的不一致程度最大

Conclusions

推荐使用两种最佳的方法(assessment和Mean top 50%)。对标分析(benchmarking analysis)也表明，发展一种新的pathway-level的整合方法是有空间和必要性的。

Background

​ 基因芯片维度非常高,现在主要有两种方法做pathway分析:ORA和GSEA.这两种功能富集分析的共同主题是，首先对单个基因进行差异表达测试，然后在pathway水平结合产生的基因水平结果，以识别差异调控的pathway。

​ 另一种替代方法也是可能的，基因表达数据首先在pathway水平整合，以产生原始数据的紧凑表示，其中数据矩阵中的每一行现在对应一个pathway，而不是一个基因。什么是以产生原始数据的紧凑表示. 然后，直接分析pathway-level的整合表达数据，或简单地说，pathway表达数据，以识别差异表达的pathway。基于整合的方法的一个显著优势是，它可以应用于比传统的功能富集分析更广泛的分析任务.这是因为，一旦将基因表达数据聚集到pathway层面，pathway表达数据不仅可以用于识别差异表达的pathway，还可以利用现有的通常应用于基因表达数据的算法，对pathway空间中的样本进行分类或聚类.将表达数据从基因空间转换到pathway空间也有望产生更稳健的数据表示，其中样本之间的内在技术和生物方差减少.换句话说，尽管表型特征相似的样本中，pathway中单个基因的表达可能存在很大差异，但pathway的整体表达可能在样本中变得一致。几项研究提出了基因表达数据的pathway-level整合方法，指出了这些方法在可解释性、紧凑性、实用性和预期的鲁棒性方面的优势

​ 随着所有这些pathway-level整合方法的可用性，综合评估这些方法之间的比较变得非常重要。但方法发布的时候都说自己对现有方法是一个改进,但是这个评价的程度很有限,不足以提出一般性建议.因为这里有两个主要的限制:

1. 第一个限制是,在pathway空间评估分类精度的研究中，对相关但独立的测试数据集的准确性的外部验证要么跳过(或仅适用内部交叉验证),或者对有限数量的数据集(只有两对训练数据集和测试数据集)做得不够充分。 尽管内部交叉验证是评估分类器在单个数据集当中的性能的一个方便的解决方案,但是它会导致比在具有相同表型类的新数据集中实际期望的更高的性能估计.因此，在任何分类研究中，越来越多的人认识到，外部验证从独立测试数据集上构建的分类器的性能是至关重要的，以便对分类性能和泛化性进行现实的估计.为了确保综合评价、培训和外部验证需要在多种训练和测试数据集上进行,这些数据集包含广泛的表型,在表型类之间的生物学差异中,有不同程度的相对微妙。
2. 第二个限制是，所有的原始报告都没有评估具有相同表型类的数据集之间pathway差异表达特征的相关性程度. 如前所述，对pathway水平聚集的一个预期是，尽管基因的差异表达特征可能在相关数据集之间显示出一些差异和不同，但pathway的差异表达特征可能会变得更加一致。尽管pathway特征的相关程度作为一种评价指标很重要，但在原始报告中并没有对其进行评价。

​ 为了解决上述对可靠评估的局限性，本研究对六种最显著的基因表达数据pathway水平整合方法(五种现有方法和一种现有方法的简单变体)进行了综合评估。用于基准测试的数据集由7对不同表型的两类基因表达数据集(共14个数据集)组成。基因表达数据集聚集在space of KEGG pathway。通过内部和外部的分类准确性验证，以及pathway特征的相关性，评估了pathway-level整合方法的性能。

内部有效性是关于实验本身的， 讨论 往往是实验设计是否合格，统计方法是否正确， 得出的结论是否具有统计意义等等。 在讨论Internal Validity 我们关心的是实验是否真的找出了因果关系。

外部有效性指的是， 你的研究在多大程度上进行外推。 把你的研究成果用于不同的人群，不同的时间， 不同地点等等。 可以预见到， External Validity 越好的因果关系价值越高， 因为人们可以在更多的场景下使用它。

Results

表1

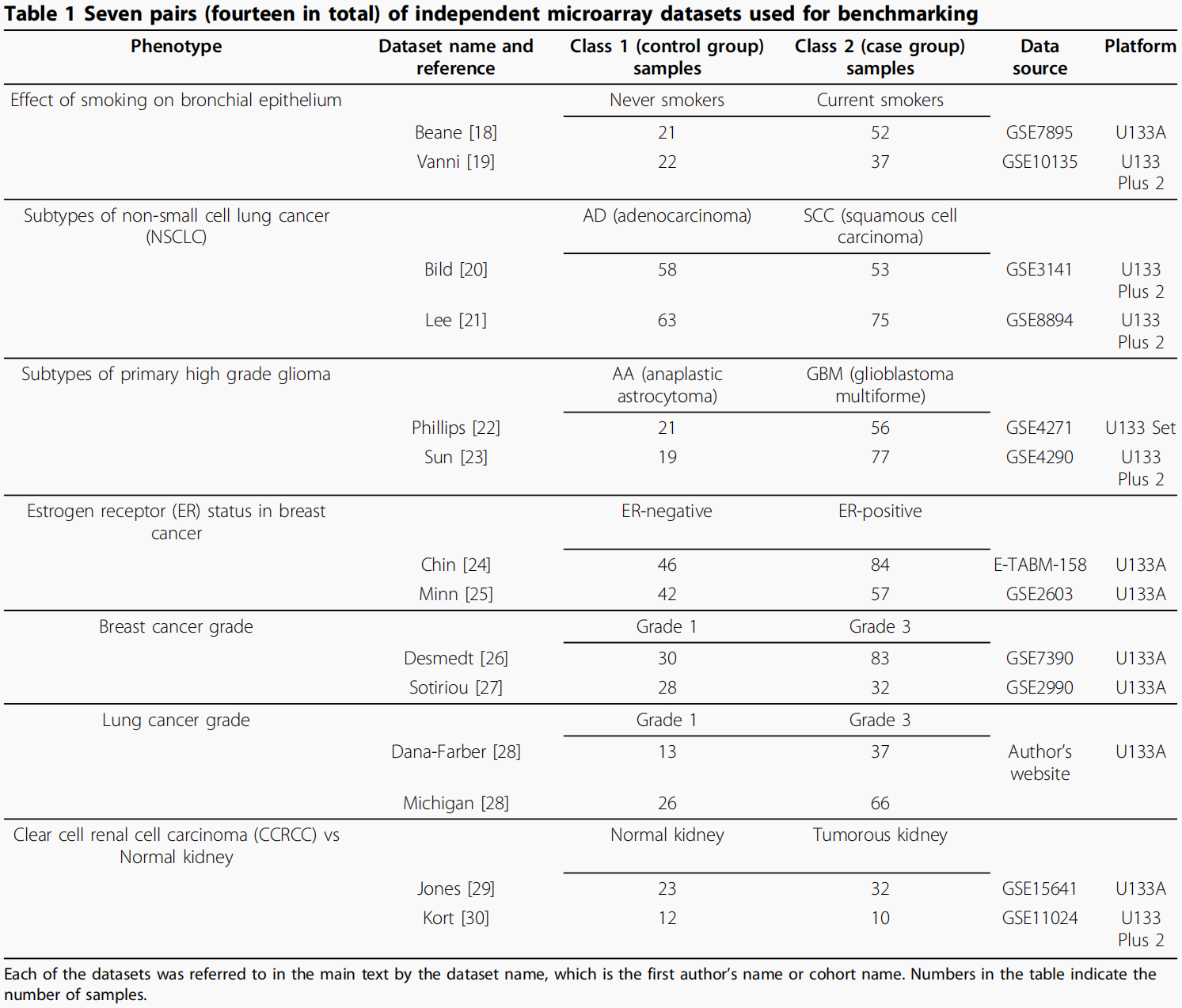
​ 本研究比较了六种最著名的基因表达数据pathway水平聚合方法。为了说明性的目的，提供了由六种方法聚合的基因表达谱和相应的途径表达谱的示例作为热图:

图1

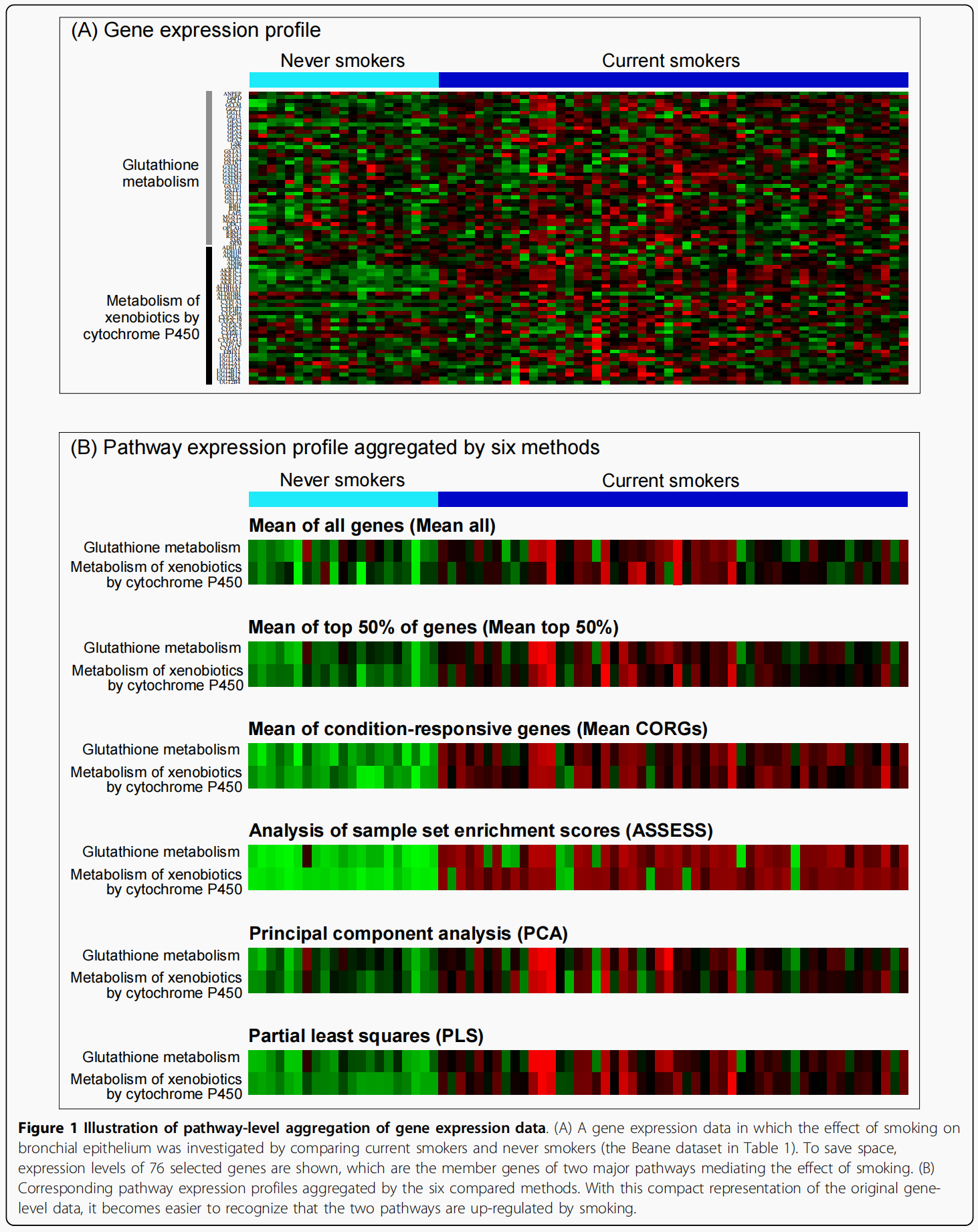
下面是一个示例,展示六种方法的结果,这六种方法可以被分成三类:

1. 基于均值的(mean of all genes, mean of condition-responsive genes, and mean of top 50% of genes)
2. 基于投影的(PCA , PLS)
3. other(analysis of sample set enrichment scores)

对每一种方法的描述:

1. Mean of all genes(Mean all)

​ 用这种最直接的方法，这种方法在文献中以这样或那样的形式出现过很多次，基因表达数据首先对样本中的每个基因进行z轴缩放，使其均值和单位方差为零。然后取一个pathway中所有成员基因的均值，将它们的表达谱组合起来。

2. Mean of condition-responsive genes (Mean CORGs)

​ 在这种方法中，pathway的表达谱(expression profile)由关键成员基因CORGs(条件应答基因)的平均表达来表示，而不是所有成员基因。CORG (condition-responsive genes)被定义为通过平均整合它们的表达谱，产生数据中两类pathway表达谱中最具区别性的基因。在给定的两类数据集中确定pathway的CORG首先要对属于给定pathway的基因的z-sacled表达数据进行t检验.然后,在pathway中表达变化的总体方向(即上调或下调)被确定为其所有成员基因的平均t统计值的符号. 然后，根据pathway的总体调控方向，将此pathway所有成员基因的t统计值进行排序;上调最强烈的基因被排列在顶部，形成整体上调pathway，而下调最强烈的基因被排列在顶部，形成整体下调pathway。

​ 然后开始迭代,像这篇文章一样 这里 .虽然这种方法在原始文献中被称为PAC(Condition-responsive genes)，为了强调该方法的Mean -based性质，也为了避免与本文评估的PCA (principal component analysis)方法混淆，本报告将其称为Mean CORGs.

3. Analysis of sample set enrichment cores (ASSESS)

​ ASSESS可以被认为是GSEA的一个样本水平的拓展.与GSEA方法一样，ASSESS计算每个途径的富集分数。不同之处在于GSEA只给出两类样品之间pathway的总体富集分数,ASSESS提供了每个样品的pathway富集评分.为此，ASSESS使用了两次随机游走计算。随机游走的第一次应用是在单个基因的水平上.给定样本中某一基因的表达水平，计算该样本属于一类而不是属于另一类的log likelihood ratio.要计算log likelihood ratio，首先需要计算样本中一个基因表达水平代表第1类或第2类的两种概率。随机游走用于此概率计算。关于第一次使用随机游走的更详细描述可以在原始文献中找到.然后在每条pathway的层次上进行第二次随机游走。使用为其成员基因获得的log likelihood ratio，它通过从零随机游走的最大偏差计算样本中pathway的富集分数，如GSEA。

4. Principal component analysis (PCA)

​ 在这种用法中,首先对z-scaled的基因表达数据进行PCA分析，得到相关矩阵.相关矩阵中的每一个元素都表示对应的基因对之间的依赖性，零表示独立性.然后，通过对相关矩阵进行特征分解，将数据中变异性最大的主要方向识别为相关矩阵最大特征值对应的特征向量.或者，等价地，相关矩阵的特征向量和特征值也可以通过奇异值分解得到(SVD)的基因表达矩阵本身。特征向量在基因表达研究中被称为主成分(PCs)或元基因。最后，将基因表达数据投影到少数pc上，通常是2个或3个，这些投影用于数据的探索性可视化.PC的矩阵通常被称为载荷，其中每一列给出了每个PC轴相对于原始轴系的位置。投影矩阵通常也被称为分数，其中每一列给出了样本相对于PC轴的位置。

​ PCA还在一些研究中被用作一种pathway-level整合方法。在这种用法中，通过将PCA应用到给定pathway中成员基因的z-scaled表达水平矩阵，而不是微阵列中代表的所有基因，来发现PCs.将该pathway的基因表达数据投影到的第一个PC上作为该pathway的表达谱.在PCA作为一种pathway-level整合方法的应用中，值得注意的是存在一个被称为符号模糊[16]的问题，这是尽管PCA被广泛使用，但在生物信息中,它是固有的且经常被忽视的方面.符号模糊是指主成分分析(PCA)和奇异值分解(SVD)的一种内在属性PCs，或者说是奇异向量，在数学上无法确定.考虑这个矩阵\(X\) 的分解, \(X = UΣV^T\),其中\(Σ\)为对角矩阵，\(U\)和\(V\)的列分别为左奇异向量和右奇异向量(\(X ∈ \mathbb{R}^{I * J }\) , \(U = \{ u_1,u_2,...,u_I\} ∈ R^{I * I}\), \(V = \{ v_1,v_2,...,v_J\} ∈ R^{J * J}\) ).在这种分解中，只要相应的左奇异向量的方向翻转，任何右奇异向量的方向都可以翻转. 换句话说，下面的等式对于任何列索引k都成立; \(σ_k\bold u_k\bold v^T_k = σ_k(−\bold u_k) (−\bold v_k)^T\) .尽管PCA和SVD的任何实现都将特定的符号分配给奇异的向量，符号的分配本质上是随机的.注:这个点没看懂,可能需要看这篇文献 . 在pathway-level整合的背景下,这意味着,对于通过PCA获得的pathway expression profile,pos和neg的表达值不一定意味着上调调控和对pathway的下调.PC值的正负符号缺乏有意义的生物学解释。虽然在一些研究中没有得到认可,但使用PCA作为一种pathway-level的整合方法, 通过纠正PC分数的正负符号,它被考虑在其他相关研究使PC得分与给定模块的平均基因表达情况呈正相关.本报告所示的分析采用了这种简单的符号校正方法。

5. Partial least squares (PLS)

​ PLS是一种结合多元回归和主成分分析法的回归方法。PLS分析的数据由数据矩阵X和响应矩阵Y组成，分别包含自变量和因变量的值.简而言之，PLS试图找到潜在变量(相对于观察变量)，最好地总结了原始数据X的方差，是最相关的响应Y。与标准的多元回归建立原始数据X和Y之间的回归模型不同，PLS寻求建立X和Y的潜在成分得分之间的回归模型.与主成分分析(PCA)不同，主成分分析选择PC，以便只有在X内的可变性是最好的描述，PLS选择潜在成分，以便在X和响应Y之间的协方差是最好的描述。之前的一项研究使用PLS作为一种pathway-level整合方法。在这种方法中，数据由给定pathway成员基因的z-scaled表达水平矩阵X和类向量Y组成。类向量中的每个元素只是表示对应样本的类成员关系。将第一潜在分量的得分向量作为该pathway的表达谱。在主成分分析的情况下，潜在成分的标志需要得到进一步的考虑.在之前的研究中，我们使用一个虚拟编码方案来表示类向量，0代表控制样本，1代表案例样本.然而，在这种编码方案下获得的潜在成分的符号缺乏有意义的生物学解释。由于1是一个比0更大的数值，对这两个虚拟数值的回归使结果pathway表达水平在案例样本中更大，在控制样本中更小.因此，后续的pathway水平差异表达分析将错误地识别所有pathway上调。因此，在本报告中所示的分析中，对潜在成分评分的符号进行了修正，使评分与给定pathway的平均基因表达谱呈正相关——使用相同的校正方案主成分分析.这种校正方案也相当于对整体上调pathway使用0/1编码，对整体下调pathway使用1/0编码。

6. Mean of top 50% of genes (Mean top 50%)

除了上述五种现有方法外，本报告还提出了第一种方法的简单变体(所有基因的平均值)。在这种修改中，pathway表达谱的计算方法是只取t统计量较大的成员基因的上半部分的平均值，而不是所有成员基因的平均值。

Collection of benchmarking datasets

为了进行综合评价，我们总共收集了7对不同表型的独立数据集，共14对(表1)。每个数据集将以对应文章中的第一作者名称或队列名称进行引用。在所有的数据集中，第2类代表了比第1类更恶性的样本组。因此，2类为病例组，1类为对照组。

每个数据集的内部交叉验证准确性

pathway表达谱鉴别两个样本组的能力首先在每个数据集中通过5倍交叉验证进行评估 (Figure 2).Balanced accuracy检验作为一个功能的特征集大小.(从前一个到十个pathway，通过pathway-level整合数据的t检验排名)，而不是固定的任意数量的特征，或优化的特征数量，结果在验证数据集中的最佳性能

$Accuracy = \frac{tp + tn}{tp + tn +fp + fn} $

精度在不平衡的数据集中表现的不好,例如你有95个负样本和5个正样本.把所有的样本都分类为负的你也有0.95的精度分数.而Balances Accuracy(bACC)克服了这个问题,通过将正负样本的数量来吧tp 和 tn的预测值正则化, 再将两者加起来了除以2.

\(Balances Accuracy = \frac{TPR + TNR}{2}\) , 其中 \(TPR = \frac {TP}{P} = \frac{TP}{TP + FN}\) , \(TNR = \frac{TN}{N} = \frac{TN}{TN + FP}\) ,\(P\) 是真pos的样本数,\(N\) 是真neg的样本数.

这时再用之前的例子,将所有的分类为neg，会给予0.5的balance accuracy评分(最大的bACC评分为1)，这相当于平衡数据集中随机猜测的期望值。balance accuracy可以作为一个模型的整体性能指标，无论真实的标签是否在数据中是不平衡的，假设FN的成本与FP相同。

​ 下图的意思是:作者做每个数据集内部的交叉验证,用每一个方法在每一个数据集中都做一次分析,把得到的pathway set按照pathway的t-score排序,然后逐渐在分类器中根据t-score添加pathway,从一个添加到十个,以此来看不同的分析方法得到的pathway set对于每个数据集内不同组的分类效果.

​

​ 做完后发现:

1. 在一些显著有区别的样本中,模型普遍表现优良

2. 在不同的样本大小的数据集中,accuracy有显著的波动.Mean all, Mean top 50%, and ASSESS这些方法波动小，Mean CORGs, PCA, and PLS这些方法波动更大。

3. PCA方法没有一次达到最高的accuracy.

图2

图9

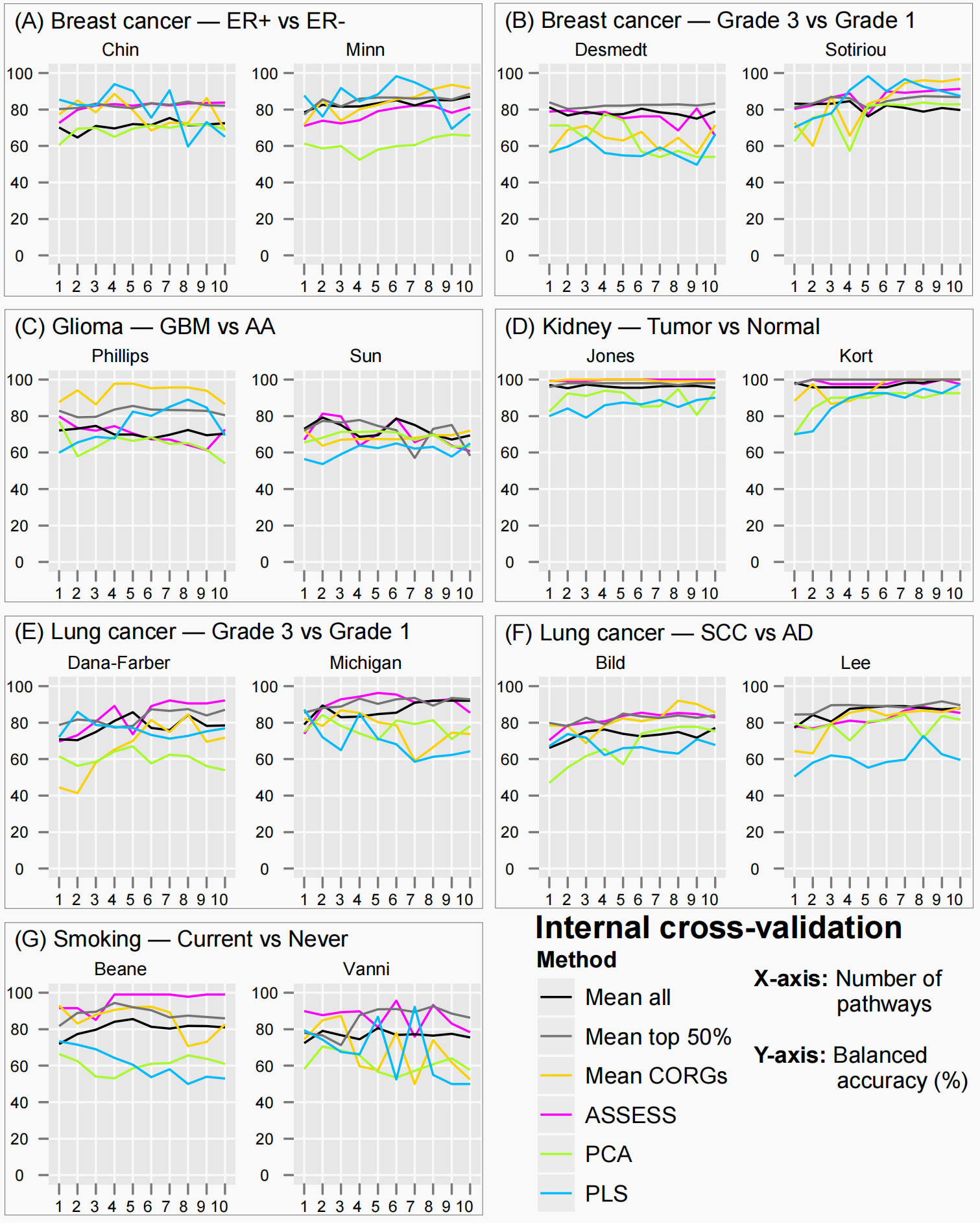
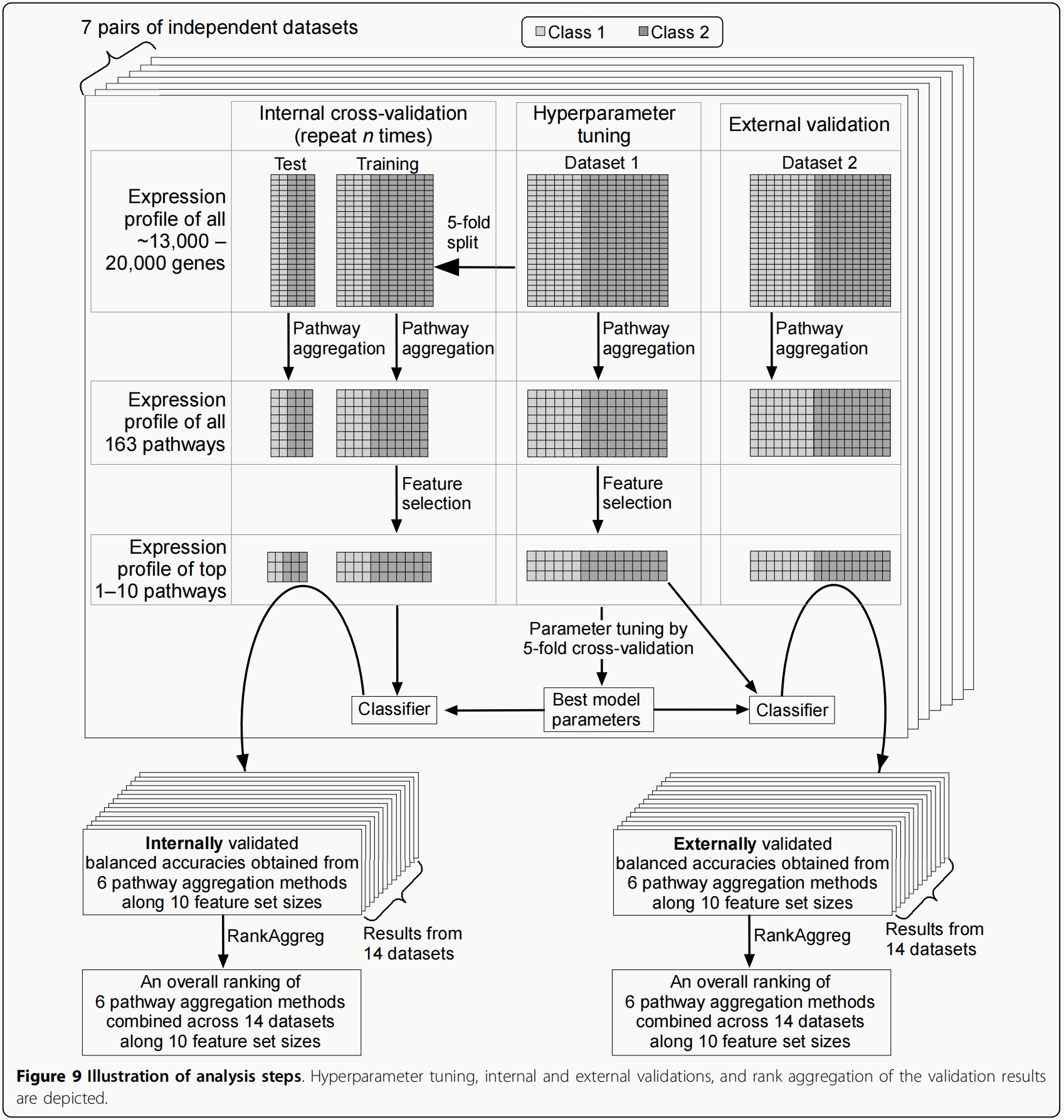
图9是做各种验证的方法，感觉这是个好办法

每对数据集的外部验证准确性

​ 使用cross-validation检查每一个分类器的准确性之后,然后通过外部验证具有相同表型类别标签的独立数据集来重新评估准确性(这句话没看懂,但是我看图的意思是还用上面的7组数据,只不过换一种test方式).在内部验证中，似乎有更明显的波动在(Mean CORGs, PCA, and PLS) than in the rest (Mean all, Mean top 50%, and ASSESS).除了上述定性观察之外，由于准确性上存在数据集依赖和特征集大小依赖的波动，因此很难进一步定量地比较这六种方法的相对性能.例如，虽然比较乳腺癌ER亚型数据集中显示相对较小波动的方法应该是相对简单的,但在吸烟数据集中很难这样做，因为它显示了很大程度的波动.为了便于进一步的比较，我们使用一种基于排名的方法来获得所有数据集的准确性汇总视图，如下一节所述

图3

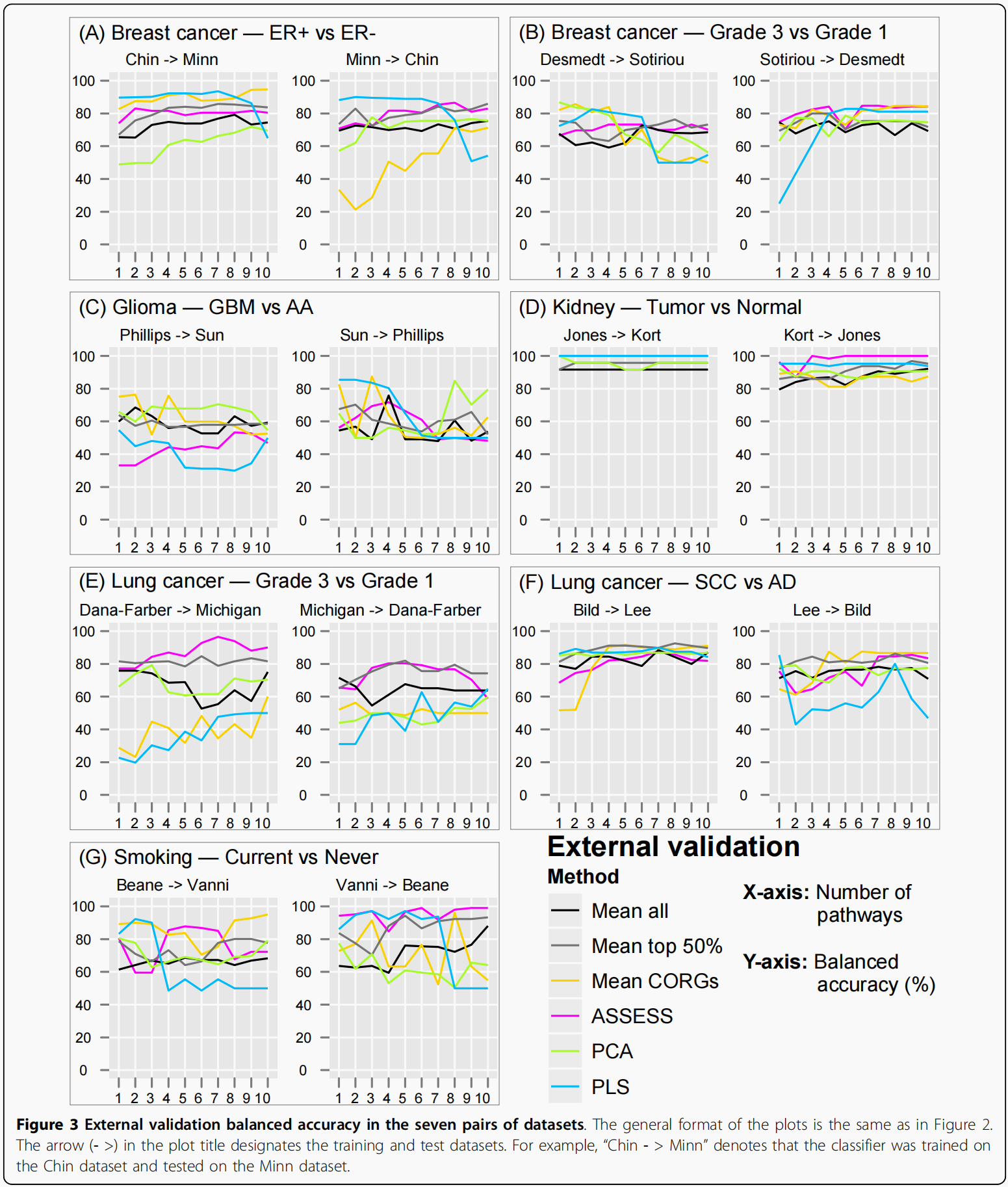
综合数据集的整体准确性排名

​ 为简化两种方法的比较，将6种方法在每个数据集上的排序结果进行汇总，并将14个数据集上的排序结果进行合并.为此，我们使用了RankAggreg包，当给出多个排名列表时，它会生成一个组合排名列表。对外部验证结果和内部验证结果分别进行排序组合。下图显示了六种方法在每个特征集大小上的组合排序。Internal cross-validation是A,External validation是B

图4

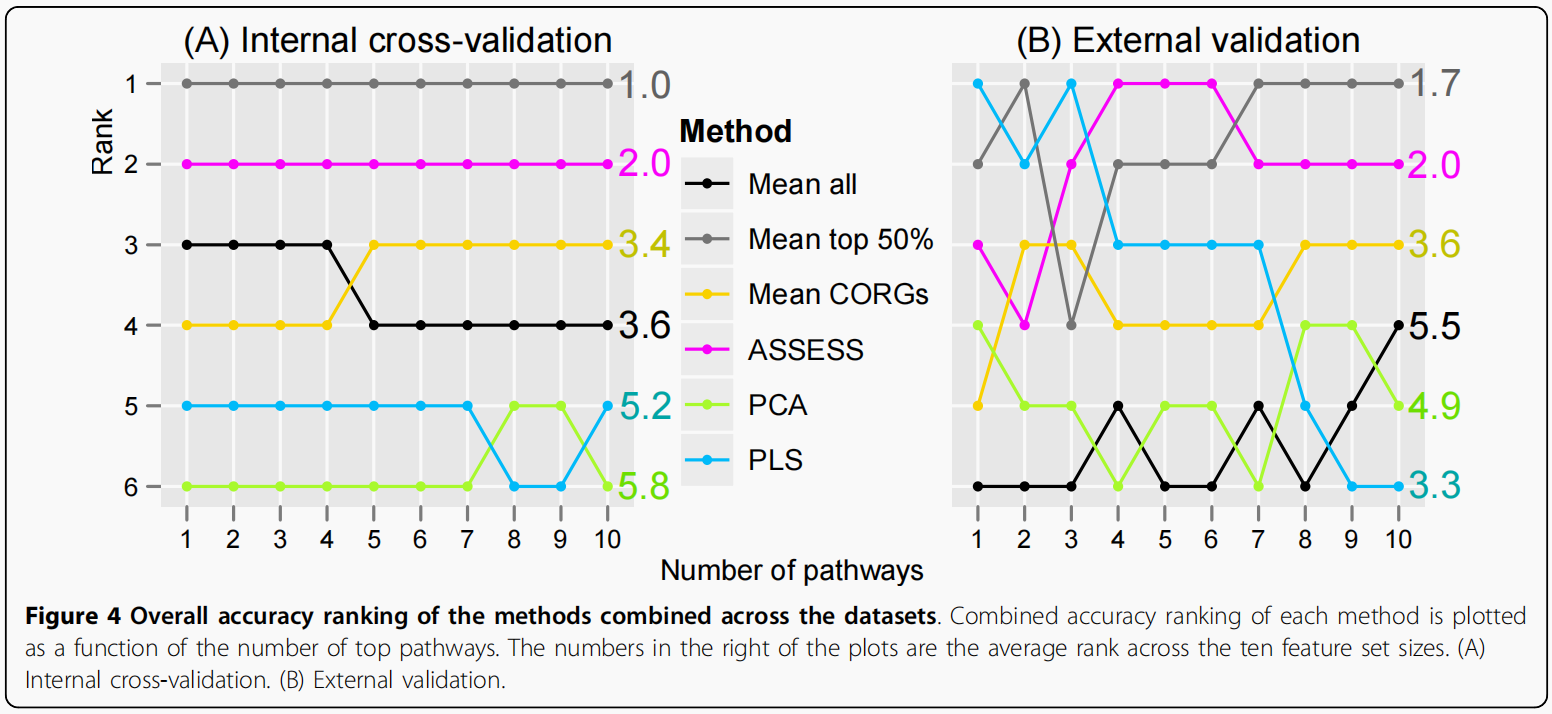
​ 有了这种基于排名的概括表示，六种方法的相对性能变得更加明显。意味着Mean top 50%在所有特征集大小中获得了最高的精度排名，而PCA获得了最低的精度排名.总体而言，尽管个别数据集内的精度值存在波动，但综合精度排名在内部验证中只显示出很小程度的波动。在外部验证中(B)，综合准确度排名有相当大的波动。然而，尽管有波动，六种方法的相对性能是可区分的.通过比较图B和图A，可以观察到外部验证和内部验证结果大致相似。首先,平均而言,Mean top 50%在外部验证(平均rank为1.7)和内部验证(平均rank为1.0)中准确率最高.第二,PCA在外部验证中排名第二(平均等级为4.9)，内部验证最低(平均等级为5.8)。第三，两个验证的平均CORGs均达到中等精度。第四，在两个验证中，ASSESS的准确率排名第二.另一方面，也可以在外部和内部验证结果之间进行不同的观察。例如,尽管PLS在内部验证中始终处于接近底部的位置，在外部验证中，随着更多的pathway加入分类器，其准确率排名稳步下降，平均排名为3.3 . 而内部和外部验证的结果既有相似之处，也有不一致之处.外部验证的结果应该得到更大的权重，因为外部验证是估计分类器的真实性能和泛化性的更现实的方法，如Introduction部分所述。因此，在随后的章节中，只对外部验证的结果进行了分类性能的进一步检查。

跨数据集和特征集大小的准确性总体分布

​ 为了进一步总结图3所示的外部验证结果，我们将所有14个数据集和10个特征集大小下的6种方法的准确率进行了池化，得到了每种方法的总体准确率分布，并表示为箱线图(图5).

池化(pooling) : 目的是为了减少参数,在极小的范围内保持某种不变性(旋转不变性,平移不变性,伸缩不变性等).

图5

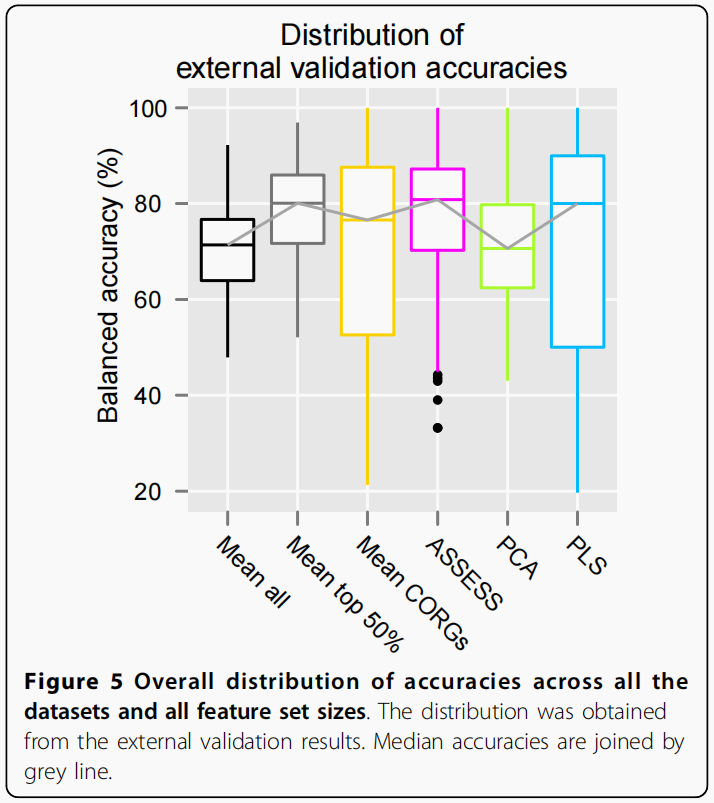
​ 关于中位数精度，有三种方法(Mean top 50%，ASSESS，和PLS)同样显示更高的准确性(约80%)，而Mean all和PCA的准确率较低(约70%).关于离散度(dispersion)，有四种方法(Mean all，Mean top 50%， ASSESS和PCA)显示相似的离散程度，而Mean CORGs和PLS显示高度的离散程度,低四分位值很小(约50%)(这个离散度可以理解成方差,方差越大说明波动越大,不好)。考虑到中值精度和离散度，Mean top 50%和ASSESS在所有数据集和特征集大小上都表现出了类似的良好性能。尽管PLS显示了良好的中位数精度，其准确性在数据集和特征集大小上变化最大。

准确性在每个表型中的总体分布

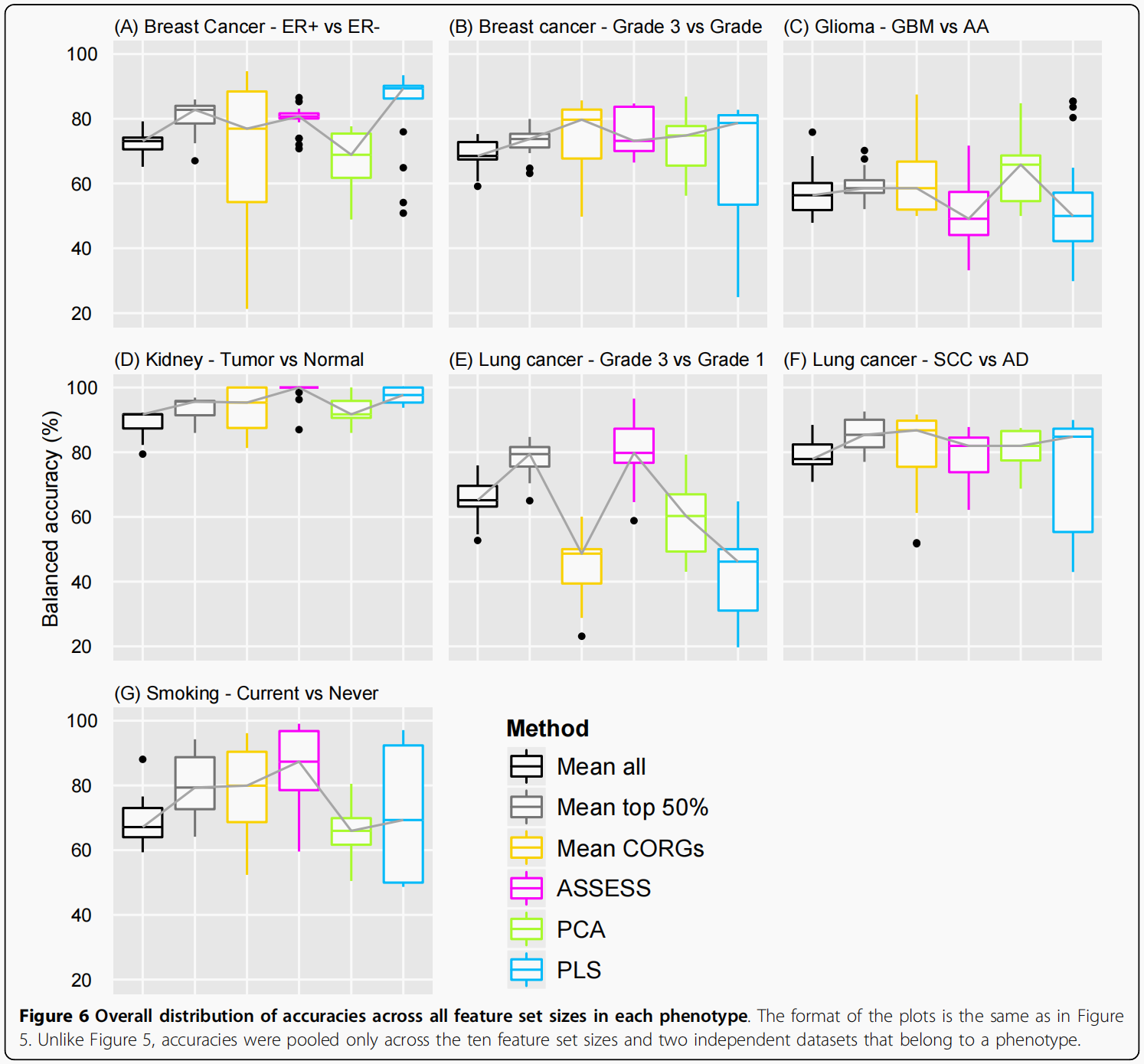
​ 图3所示的外部验证结果也通过汇集它们在所有特征大小和每个表型中的两个独立数据集上的准确性对每一种方法进行了总结(图6)。一个主要观察结果是，不同表型的方法的相对性能不同.虽然所有方法的中位数准确性在某些表型中相对相似(图6B，D和6F)，其他表型也有很大差异(图6E和6G)。这一观察结果意味着，性能评估应该在尽可能多的表型中进行，就像本研究中所做的那样。

图6

pathway差异表达统计数据集之间的相关性

​ 方法的比较也可以通过评估pathway的差异表达统计数据在独立数据集之间的相关程度来进行。为此，我们对pathway表达谱进行Student’s t检验，以获得每个数据集中每个pathway的t统计量.每种方法总共获得7对pathway特征。因此，对于一个给定的表型，可以将一个pathway在一个数据集中的t统计量与它在另一个数据集中的t统计量相关联。通过将7对数据集之间所有pathway的t-统计值关联起来，为每种方法制作了t-统计量的散点图，以获得一个汇总视图(图7)。

图7

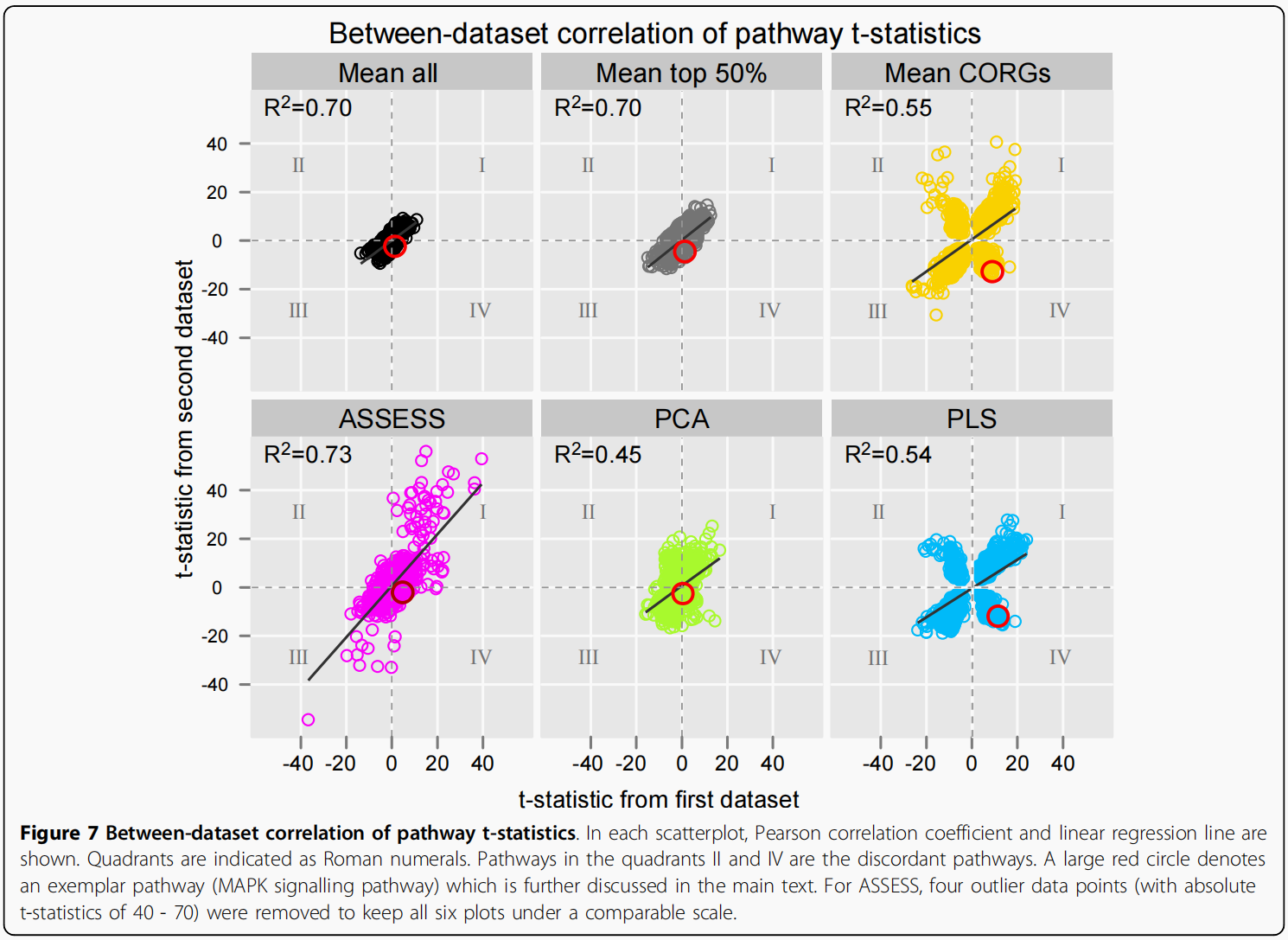
​ 因此，每个图包含1141个数据点(163个通路乘以7个表型)。从散点图可以得出两个主要的观察结果.在三种方法下观察到的相关性(cogs、PCA和PLS)低于其他(Mean all，Mean top 50%，ASSESS)。其次，相关性较低的三种方法在两个独立的数据集(象限II和IV)之间存在许多不一致的pathway，这些pathway的t统计量很大，符号相反。正是这些不一致的pathway，当用作特征时，降低了外部验证的准确性，并导致了观察到的准确性波动，如图3所示。

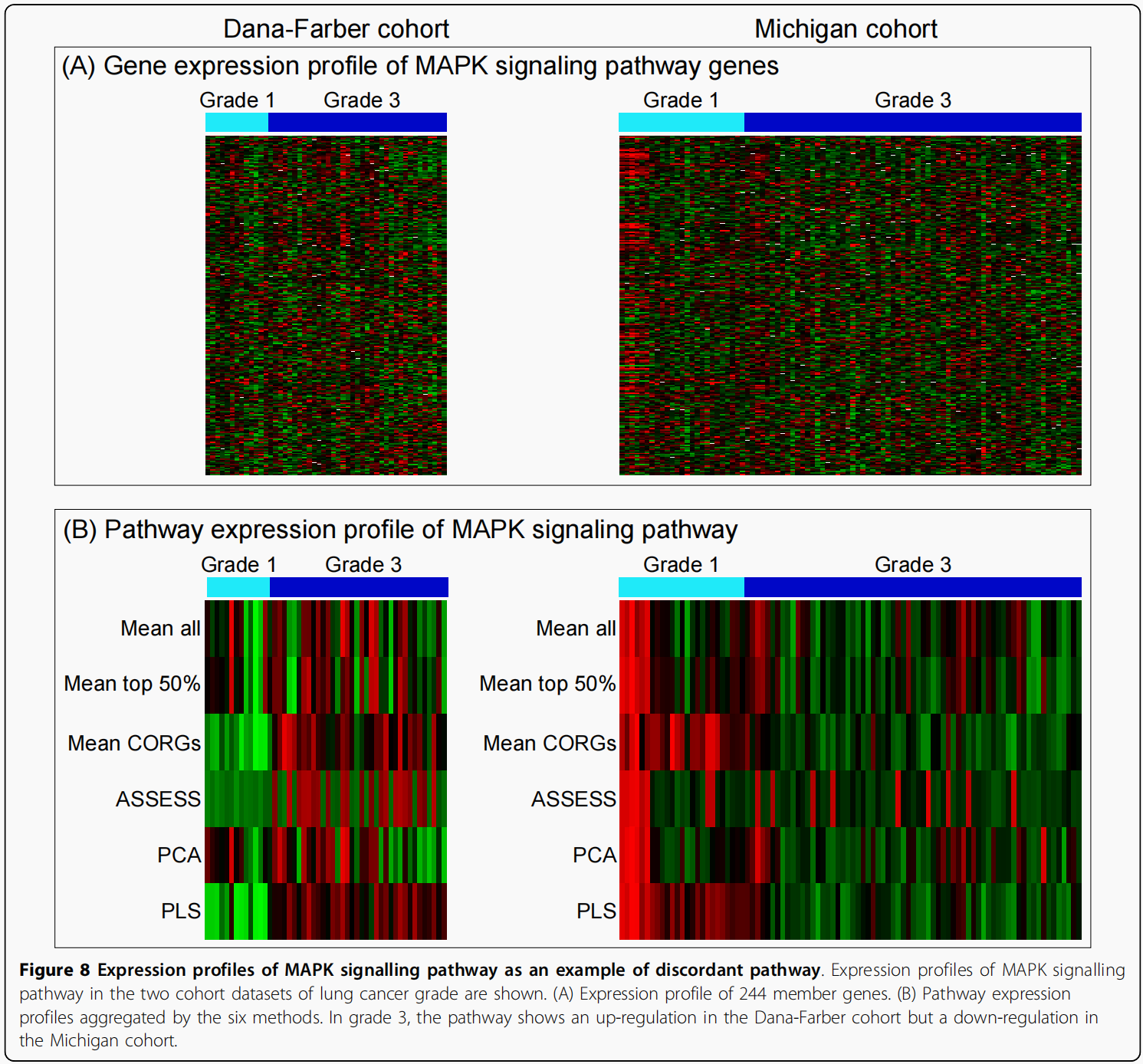
​ 为了进一步研究不一致通路，在分类分析中使用的前10个特征通路中选择了一个范例通路。因为肺癌分级数据集显示出较低的准确性(图6E)三种方法(平均CORGs，PCA和PLS)比其他方法，从肺癌分级数据集中的特征通路中选择了一个样本通路.其中一个最不协调的pathway与最大的t统计值大小是MAPK信号通路，其244个成员基因在基因芯片数据中表示。在Mean CORG中，它是一个数据集中上调最多的通路(Dana-Farber)，但在另一种(Michigan)中是第五大下调通路(数据未显示)。在PLS中，它也是Dana-Farber数据集中上调最多的通路，但在Michigan数据集中下调通路排名第21位(数据未显示)。其在肺癌分级数据集中的t统计数据如图7中红色大圆圈所示，通过六种方法聚合的其成员基因表达谱及其通路表达谱如图8所示.(作者这样写的思路是: 在对照组上调最大的通路,在实验组却没有什么下调,这样可能是造成External Validiton correlation不是很高的原因).

从图8中可以观察到三个现象：
首先，通过通路表达谱，组之间的表达差异变得更加明显(图8B)比基因表达谱(图8A).
第二，两个队列数据的通路水平表达变化方向不一致。在Grade 3组中的样本，MAPK信号通路在Dana-Farber队列中上调(图8B，左)，但在Michigan队列中下调(图8B，右)。
第三，通路的差异表达程度在Mean CORGs和PLS方法上表现的更显著，因为所有的样本在每个组显示相对均匀的表达水平。

图8

Discussion

​ 本研究评估并比较了基因表达数据通路水平聚合的六种方法——五种现有方法(Mean all、Mean CORGs、assessment、PCA和PLS)以及现有方法的一种简单变体(Mean top 50%).四种比较方法是传统的降维方法(PCA和PLS)或简单启发式(Mean all and Mean top 50%)。这四种方法并不是专门为处理pathway-level整合问题而开发出来的.可以说，前者缺乏坚实的生物学basis，后者则缺乏formal basis。其他两种方法(平均corg和ASSESS)是特定于路径级聚合问题的。通过对7对相关但独立的数据集之间路径签名的相关程度进行内部和外部验证，评估了分类准确性。结果表明，两种方法在性能上存在较大差异。本研究的三个主要发现如下所述。首先，就外部验证精度而言，6种方法从高到低依次为Mean top 50%、ASSESS、PLS、Mean CORGs, PCA和Mean all(图4B)。降维方法总体上表现较差。其次，在Mean corg和PLS中，准确率的总体分布是倾斜的(这里应该是指方差大)(图5)，表明这两种方法在很多情况下表现不佳。第三，这两种方法在这种情况下表现不佳的原因是它们倾向于产生相关但独立的数据集之间不一致的pathway expression signatures，如pathway t统计相关性(图7)所示。两种方法的算法特点导致数据集之间不一致。在Mean CORGS,该通路表达变化的总体方向首先被确定为其所有成员基因平均t统计值的符号。然后，只选择对通路水平t统计量贡献最大的关键成员基因.因此，如果通路的整体表达变化在数据集之间的不同方向上，即使是很小的量级，结果通路表达谱中的不一致性就会变得夸大 确实有这个问题，如果整体偏差不大，那么选出来的方向可能是不对的，进而筛选到的就有很大的几率是错误的 。同样，在PLS中，对潜在成分的正负符号进行了校正，使成分得分与给定通路的平均基因表达谱呈正相关。因此，PLS聚合的通路表达谱在相反的方向上也变得不一致。

​ 上面描述的第三个观察结果表明，为了得到一个在独立数据集和表型预测之间一致的通路表达谱，因此，一个成功的通路水平聚合方法不应该严格依赖于通路表达变化的总体方向，而应通过其成员基因z尺度表达水平的平均值来衡量。尽管这是最简单、应用最广泛的实践，即认为一个通路在平均表达为阳性时被上调，在平均表达为阴性时被下调，但这样的理论基础缺乏坚实的生物学支持.有人认为，在生理过程中，如生物通路，可能会发生稳态转录反应，因此通路中一个成分的上调会导致该通路中另一个成分的下调，以试图补偿.如果由于某种原因，两个通路成分的相对大小在独立的数据集之间发生逆转，那么在相反的方向上，通路表达变化的总体方向就会变得不一致.此外，考虑到通路下游基因的差异表达可能不会像其上游基因那样影响通路的整体活性，因此，将所有成员基因的表达变化简单地平均起来，就好像它们是独立的、统一的对象一样，可能无法得到一个充分的衡量方法来代表通路在生物学背景下的表达行为.因此，我推测，一个成功的通路水平聚合方法需要考虑通路的稳态反应、基因在通路拓扑中的位置以及成员基因之间相互作用的类型等问题。最后两个问题也在一篇描述基于拓扑的途径富集分析方法的综述论文中被提及.

​ 通路级聚合方法的优势在于，它不仅可以用于识别差异表达的通路，还可以用于在通路空间中对样本进行分类或聚类，获得原始基因表达数据的紧凑表示和可视化，以及促进系统级解释.然而，路径级聚合方法的一个固有问题是原始基因表达数据中存在的信息可能丢失甚至变形.这个问题的出现是因为通路成员基因的表达水平被降低到一个单一的数值。在这方面，通路表达谱的辨别能力与通路大小之间可能存在一种关系，因为通路大小可能表明通路的复杂性或表征程度。为了检验这样的关系是否存在，对14个数据集中的每一个，163个路径按t-test p值排序。在每个级别上，准备一个box plot来总结14个数据集中该级别路径的大小。然后将路径的中位数大小连接起来，以显示大小和秩之间的总体趋势(附加文件2).总的来说，没有明显的趋势表明路径的规模-级别关系.另一个潜在的问题是路径级聚集的方法是可能的相互关联的途径，其成员基因部分重叠.对于这样的通路对，一个实际上与给定的表型无关的通路可能仅仅因为与其他相关且真正具有区别的pathway共享许多成员基因而被认为具有discriminative的profile.避免将这种不相关的路径识别为discriminative是我们想要的，因为它将混淆结果的解释.在功能丰富分析领域，这个问题已经通过对路径中的共享和唯一成员子集执行单独分析等方法得到解决,是个好办法,并给予在通路网络拓扑结构中处于中间位置的基因较小的权重，这些位置很可能在通路之间共享.在路径级聚合领域也可能采用类似的方法。

​ 本研究采用的评价方案有四个主要优点，提高了报告结果的有效性.首先，评估是综合的，因为使用了7对相关但独立的数据集。在包含各种表型的大量数据集下评估性能有助于得出一个一般化的结论。如图6所示，七种表型的中位数和准确率分布都不同。如果只用表型来源的数据集被用于基准测试(例如，图6D和6F)，这将是错误的结论，六种比较方法没有不同的中位数精度也就是你只用这个算法首次被提出来的那篇文章对应的数据去做测试,那么得到的精度是不准的。其次，通过外部验证独立数据集上的分类准确性来进行评估。第三，评估是透明的，因为分类精度是作为特征集大小的函数来检验的(从前1到10个路径，通过路径级聚合数据的t检验排名)，而不是固定的任意数量的特征，或在验证数据集中产生最佳性能的优化特征数量.尽管跨特征集大小的准确性的最终波动(图3)可能使性能比较不那么明显，但它们清楚地表明，排名靠前的差异调节路径的表达谱可能在数据集之间不一致.第四，通过检查数据集之间通路t统计量的相关性，也对通路特征的再现性进行了评估。其结果进一步证实了数据集之间路径特征的不一致性，尤其是在Mean CORGs和基于pls的聚合下。

​ 本研究还有三个小贡献。首先，收集7对相关但独立的基因表达数据集，可以用于基于基因表达数据的任何方法的基准分析。其次，明确指出并解决了PCA中pc符号的模糊性问题。以前一些使用PCA作为聚合方法的研究要么忽略了符号歧义问题，要么简单地指出PCA聚合的表达谱不是易于解释的，因为它没有捕捉到通路的表达变化方向.本研究明确说明了这一问题，并遵循了一种简单可行的方法来纠正PC评分的迹象，以便PC评分与通路的平均基因表达谱呈正相关.在化学计量学领域也提出了一种替代方案，该方案通过计算PC与数据集中所有数据点之间的内积和的符号来确定PC的符号。采用这种方法的初步分析没有产生更好的分类精度(数据未显示)，因此在分析中没有进一步考虑它。第三，本研究还明确说明并解决了PLS中潜在成分的符号修正问题，这在之前使用PLS作为路径级聚合方法的研究中既没有说明也没有解决

​ 根据这项研究的结果，似乎有空间和必要开发一种新的方法来进行通路水平聚集.一方面，考虑到平均所有通路成员基因的表达谱(即Mean all)的准确度最低，值得注意的是，简单地去除一半t统计量较低的基因(即Mean top 50%)导致最高的准确性(图4B)。另一方面，任何依赖于通路整体变化方向的方法，如Mean CORGs和PLS，很可能表现出独立数据集之间的不一致。这一问题需要在开发一种新方法时加以考虑和解决，因为通路水平聚合的预期之一是，尽管存在基因水平的不一致性，但通路作为一个整体的表达可能在独立数据集上变得更加一致、预测性和可重复性.

Conclusions

​ 总之，本研究评估并比较了六种方法在基因表达数据的通路水平聚合.通过收集包括各种表型的7对相关但独立的数据集，使全面和严格的评估成为可能。评估是关于分类精度的，通过内部和外部验证，并检查数据集对之间的pathway signature的相关程度.通过ASSESS和Mean top 50%获得通路水平的表达谱，获得了最好的准确性和相关性。Mean all的准确率最低。在通路特征相关性中，PLS和Mean CORGs引起的不一致程度最大。本报告的分析也暗示了发展一种新的路径级聚合方法的空间和必要性。

Methods

基准测试数据集的集合

按照以下标准搜索公共知识库和文献，收集7对独立的数据集。首先，搜索仅限于人类数据集，以简化数据处理和分析。其次，只考虑将两类未配对数据集包含到集合中。第三，只考虑使用相对较新的Affymetrix平台的数据集，即排除cDNA平台或较老的Affymetrix平台，如Human Genome U95。其原因是为了确保良好的基因组覆盖，从而可靠地表示通路成员集。第四，两个类别中的任何一个都需要包含十个或更多的样本，以方便内部交叉验证。第五，也是最重要的，应该有两个相关但独立的数据集，具有相同的表型类别标签进行调查(例如，两个数据集比较吸烟者和非吸烟者的肺组织)，由独立的实验室产生。

基因表达数据的预处理

数据从表1所示的公共存储库下载。在所有数据集中，数据都以CEL文件的形式获得，除了肺癌分级的两个数据集中，数据仅以Gene Expression的形式获得综合(GEO)系列矩阵文件。对CEL文件进行RMA预处理和log2变换。GEO系列矩阵数据已经是rma处理的形式(GSE3141)或gcrma处理的形式(GSE8894)。丢弃未加Entrez和基因符号注释的探针的表达数据(基于Affymetrix注释释放30)。然后对代表同一基因的多个探针的表达水平进行平均，得到包含以下数量独特基因的基因水平表达谱数据:13029个基因(U133A和U133A 2.0);20,315个基因(U133 Plus2);18485个基因(U133集合)。对7种表型中的3种，在不同的平台上进行了一对独立的实验。在这种情况下，我们选择两个平台中共同代表的基因，它们都是其中一个覆盖范围更大的平台的子集(即U133A中的基因是U133 Plus 2中的基因子集)，然后只使用共同基因的表达数据来分析相应的表型。

基因表达数据的通路级聚合

基因表达数据聚集在KEGG通路水平。KEGG通路及其成员基因列表来自MSigDB 3.0版本，共包含186条KEGG通路。其中，有163条路径由至少20个，最多300个成员基因组成，用于后续的路径级聚合。对于三种基于均值的聚合方法(Mean all, Mean top50%，和Mean corg)，编写了一个R代码来实现它们。对于ASSESS，它的java程序是在默认参数设置下使用的。PCA和PLS分别使用WGCNA包和PLS包中的moduleEigenegenes函数。对于PCA和PLS，对成分评分向量中的元素符号进行校正，使评分向量与给定通路的平均基因表达谱呈正相关。在聚合之前，所有方法的基因表达数据都被z-scale缩放，除了ASSESS不需要对其输入进行z-scale。

选择用于分类的特征

在这14个数据集中，特征(即pathway)首先根据学生对pathway-level表达数据的t检验的p值进行排名。然后选择Top pathway，其表达值用于后续的分类器训练和性能评估。为了透明地评估分类器在一系列特征上的表现，所选pathway的数量从1到10不等。

分类不平衡的考虑

14组数据均显示分类失衡，病例组样本数多于对照组。利用这些数据集，通常可以得到一个多数类分类器，因为传统的误分类错误率可以通过简单地将所有样本作为案例样本进行预测而降低。为了纠正分类不平衡的问题，我们采取了三种措施——两种在分类器训练中，一种在绩效评估中，如下两节所述。

SVM分类器参数整定

利用e1071包中实现的SVM进行分类。选取径向基函数作为核函数。SVM有两个参数影响决策边界，需要进行调整。它们是cost和gamma的默认值在e1071包分别是1和 选择特征数的倒数。在当前的分析中，参数调整是通过网格搜索来进行的，其中cost参数随 \(C =2^4, 2^3, ..., 2^6\) 变化，伽玛范围是cost值除以选定特征的数量。在进行网格搜索时，通过5次交叉验证来选择误差函数最小的参数值对，然后用于训练分类器来验证分类性能。在网格搜索过程中，为了防止类不平衡问题，采取了两种措施。第一，分类权重参数(class.weights)设置为类比例的反比，而不是默认的等权重，以补偿类比例不平衡的影响。其次，将错误函数参数(error.fun)设为平均分类错误，即误报率和误报率的平均值，而不是默认的误报率，默认误报率是所有误报样本的总体比例。在两种误差率下，将大部分样本分类为阳性的多数分类器会得到较高的误报率，从而产生较高的平均分类错误。

平衡精度作为分类性能的衡量标准

与训练阶段一样，采用平衡精度作为绩效指标，防范class失衡问题。平衡精度定义为真阳性率和真负率的平均值。一个majority-classifier会得到一个较低的真实负率，从而较低的平衡精度，而它的传统精度(正确分类的总体比例)可能会高得毫无意义。 意思是不平衡的样本分布，会导致一个较低的真实负率，但是这个样本分布造成，同样也会得到一个较高的传统精度。所以需要使用平衡精度来衡量才不失真

分类性能的验证

采用平衡精度作为性能指标，对分类性能进行了严格的评价，包括内部和外部验证。内部验证采用分层5次交叉验证，使每个训练集的类占比与原始数据集保持一致。在交叉验证的每次迭代中，都会重新进行pathway-level的聚合和特征选择，这被强调为交叉验证的正确实践。为了获得更稳定的交叉验证结果，需要避免特定随机分裂的任何可能的影响。

因此交叉验证重复两次，以获得平均5倍和2次重复的平均平衡精度。由于ASSESS程序是可用的GUI实现，而不是命令行版本，而且单是交叉验证实验的一次迭代就涉及总共70对训练测试集(14个数据集的5倍)，每一个都需要由ASSESS和所有其他方法在路径级聚合。对于外部验证，分类器在一个数据集上训练，并在另一个数据集上测试7对独立数据集中的每一个。

跨数据集的性能排名汇总

对于14个数据集，根据平衡精度值对6种方法进行排序。6种方法的14个排名列表通过RankAggreg包组合成一个排名列表。简而言之，这六种方法的准确度在14个数据集中按从高到低排序。在每个特征集大小下，总共得到14个排序列表。每个列表根据它们在给定的特征集大小和数据集上的准确性排列这六种方法。在每个特征集的大小上，通过将14个排序列表与RankAggreg包合并得到一个方法的组合排序。使用该软件包，以平衡精度为权重，以斯皮尔曼足尺距离为距离度量进行蛮力等级汇总。图9描述了上述所有分析步骤。

我的总结

​ 非常好的总结工作,从多个方面去衡量现在通路分析方法的优劣,并给出排名. 他的评估方法很好，在cross-validation中使用5折交叉验证，学到了。