算法刷题及总结_数组篇

二分法

//算法总结
//第一部分：数组相关
/**
*Leetcode题目35：搜索插入位置
*给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。
*示例 1:
*输入: [1,3,5,6], 5
*输出: 2
*
*示例 2:
*输入: [1,3,5,6], 2
*输出: 1
*/
//解法一：暴力法 | 时间复杂度：O(n) 空间复杂度：O(1)
public int searchInsert(int[] nums, int target) {
        for (int i = 0; i < nums.length; i++) {
            // 分别处理如下三种情况
            // 目标值在数组所有元素之前
            // 目标值等于数组中某一个元素
            // 目标值插入数组中的位置
            // 一旦发现大于或者等于target的num[i]，那么i就是我们要的结果
            if (nums[i] >= target) {
                return i;
            }
        }
        // 目标值在数组所有元素之后的情况
        // 如果target是最大的，或者 nums为空，则返回nums的长度
        return nums.length;
    }
//解法二：二分法*/ | 时间复杂度：O(logn) 空间复杂度：O(1)
public int searchInsert(int[] nums, int target) {
    int n = nums.length;
    int left = 0;
    int right = n - 1; // 定义target在左闭右闭的区间里，[left, right] {

    while (left <= right) { // 当left==right，区间[left, right]依然有效
        int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
        if (nums[middle] > target) {
            right = middle - 1; // target 在左区间，所以[left, middle - 1]
        } else if (nums[middle] < target) {
            left = middle + 1; // target 在右区间，所以[middle + 1, right]
        } else { // nums[middle] == target
            return middle;
        }
    }
        // 分别处理如下四种情况
        // 目标值在数组所有元素之前  [0, -1]
        // 目标值等于数组中某一个元素  return middle;
        // 目标值插入数组中的位置 [left, right]，return  right + 1
        // 目标值在数组所有元素之后的情况 [left, right]， return right + 1
        return right + 1;
}

滑动窗口

/**
*LeetCode209.长度最小的子数组
*给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。
*示例：
*输入：s = 7, nums = [2,3,1,2,4,3]
*输出：2
*解释：子数组 [4,3] 是该条件下的长度最小的子数组。
*/
//解法一：暴力解法 时间复杂度：O(n^2) | 空间复杂度：O(1)
public int minSubArrayLen(int s, int[] nums) {
    int result = Integer.MAX_VALUE; // 最终的结果
    int sum = 0; // 子序列的数值之和
    int subLength = 0; // 子序列的长度
    for (int i = 0; i < nums.length; i++) { // 设置子序列起点为i
        sum = 0;
        for (int j = i; j < nums.length; j++) { // 设置子序列终止位置为j
            sum += nums[j];
            if (sum >= s) { // 一旦发现子序列和超过了s，更新result
                subLength = j - i + 1; // 取子序列的长度
                result = Math.min(result, sublength);
                break; // 因为我们是找符合条件最短的子序列，所以一旦符合条件就break
            }
        }
    }
    // 如果result没有被赋值的话，就返回0，说明没有符合条件的子序列
    return result == MAX_VALUE ? 0 : result;
}
//解法二：滑动窗口：不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果 时间复杂度：O(n) | 空间复杂度：O(1)
public int minSubArrayLen(int s, int[] nums) {
    int result = MAX_VALUE;
    int sum = 0; // 滑动窗口数值之和
    int i = 0; // 滑动窗口起始位置
    int subLength = 0; // 滑动窗口的长度
    for (int j = 0; j < nums.length; j++) {
        sum += nums[j];
        // 注意这里使用while，每次更新 i（起始位置），并不断比较子序列是否符合条件
        while (sum >= s) {
            subLength = (j - i + 1); // 取子序列的长度
            result = Math.min(result, sublength);
            sum -= nums[i++]; // 这里体现出滑动窗口的精髓之处，不断变更i（子序列的起始位置）
        }
    }
    // 如果result没有被赋值的话，就返回0，说明没有符合条件的子序列
    return result == MAX_VALUE ? 0 : result;
}

双指针（快慢指针）

/**
*LeetCode27. 移除元素
给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。
不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并「原地」修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
示例 1:
给定 nums = [3,2,2,3], val = 3,
函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。
你不需要考虑数组中超出新长度后面的元素。
*/
//解法一：暴力解法 | 时间复杂度：O(n^2)
public int removeElement(int[] nums, int val) {
    int size = nums.length;
    for (int i = 0; i < size; i++) {
        if (nums[i] == val) { // 发现需要移除的元素，就将数组集体向前移动一位
            for (int j = i + 1; j < size; j++) {
                nums[j - 1] = nums[j];
            }
            i--; // 因为下表i以后的数值都向前移动了一位，所以i也向前移动一位,新的数值占据了原来i的位置，所以需要重新判断是否等于target,不然就会跳过该值可能导致错误
            size--; // 此时数组的大小-1
        }
    }
    return size;
}

暴力法（双循环）

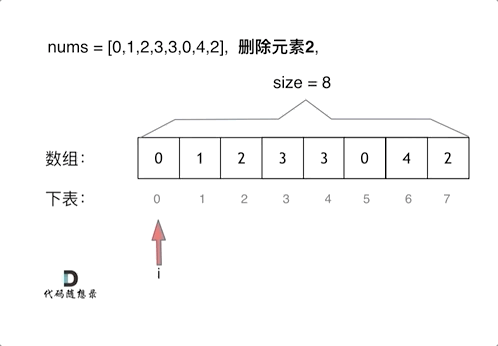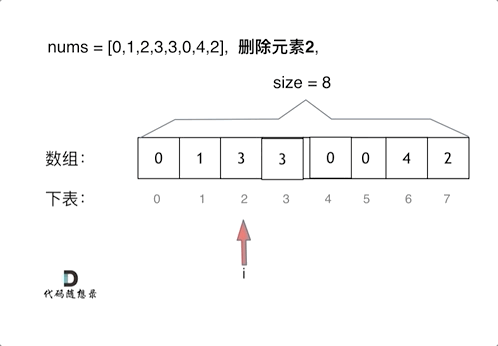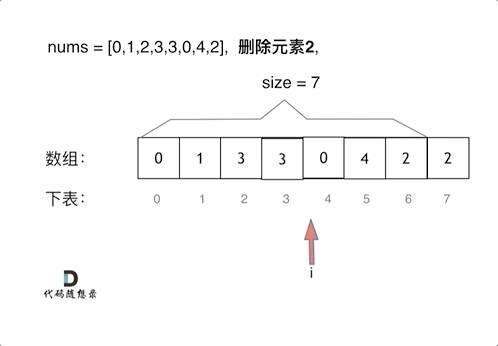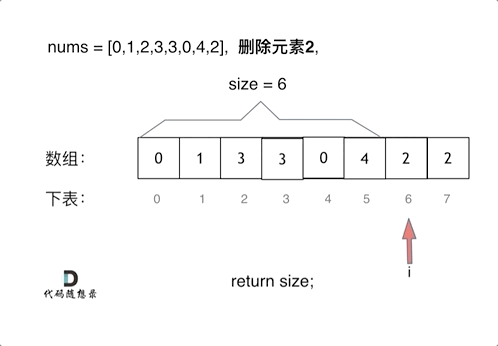
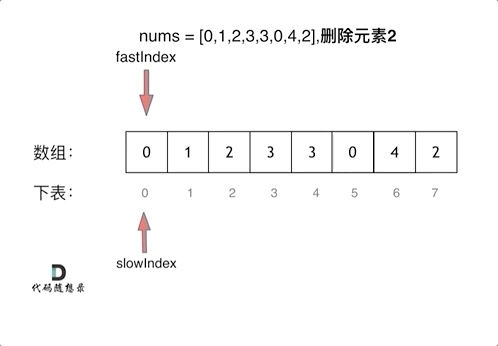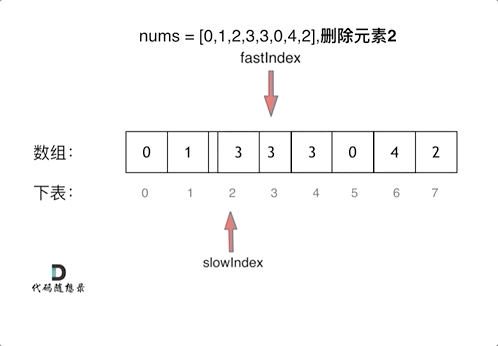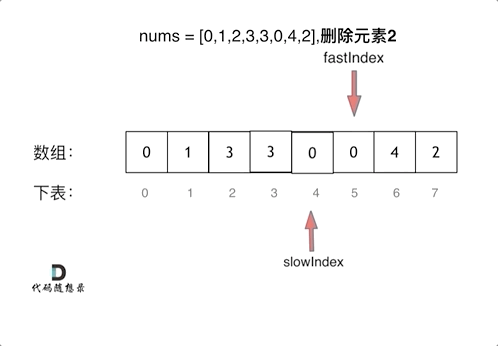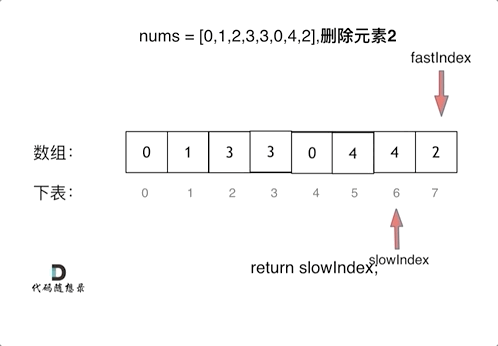
//解法二：双指针（快慢指针法）：「通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。」 | 时间复杂度为O(n)
public int removeElement(int[] nums, int val) {
    int slowIndex = 0; 
    for (int fastIndex = 0; fastIndex < nums.length; fastIndex++) {  
        if (val != nums[fastIndex]) { 
            nums[slowIndex++] = nums[fastIndex]; 
        }
    }

    return slowIndex;
}

双指针（快慢指针）

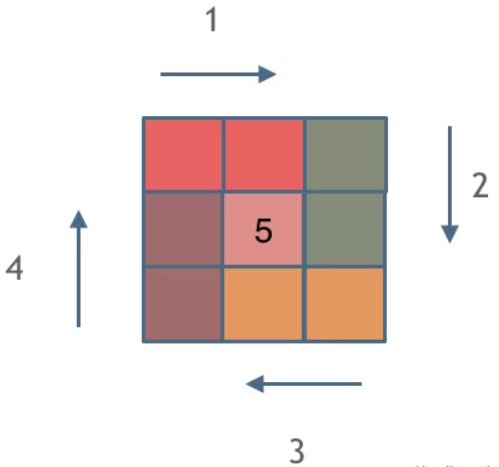
螺旋矩阵

/**
*LeetCode59.螺旋矩阵II
*给定一个正整数 n，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的正方形矩阵。
*示例:
*输入: 3 输出: [ [ 1, 2, 3 ], [ 8, 9, 4 ], [ 7, 6, 5 ] ]
*/
public int[][] generateMatrix(int n) {
    int[][] res = new int[n][n]; // 定义一个二维数组
    int startx = 0, starty = 0; // 定义每循环一个圈的起始位置
    int loop = n / 2; // 每个圈循环几次，例如n为奇数3，那么loop = 1 只是循环一圈，矩阵中间的值需要单独处理
    int mid = n / 2; // 矩阵中间的位置，例如：n为3， 中间的位置就是(1，1)，n为5，中间位置为(2, 2)
    int count = 1; // 用来给矩阵中每一个空格赋值
    int offset = 1; // 每一圈循环，需要控制每一条边遍历的长度
    int i,j = 0;
    while ((loop--) > 0){
        i = startx;
        j = starty;

        // 下面开始的四个for就是模拟转了一圈
        // 模拟填充上行从左到右(左闭右开)
        for (j = starty; j < starty + n - offset; j++) {
            res[startx][j] = count++;
        }
        // 模拟填充右列从上到下(左闭右开)
        for (i = startx; i < startx + n - offset; i++) {
            res[i][j] = count++;
        }
        // 模拟填充下行从右到左(左闭右开)
        for (; j > starty; j--) {
            res[i][j] = count++;
        }
        // 模拟填充左列从下到上(左闭右开)
        for (; i > startx; i--) {
            res[i][j] = count++;
        }
        // 第二圈开始的时候，起始位置要各自加1， 例如：第一圈起始位置是(0, 0)，第二圈起始位置是(1, 1)
        startx++;
        starty++;
        // offset 控制每一圈里每一条边遍历的长度
        offset += 2;
    }    // 如果n为奇数的话，需要单独给矩阵最中间的位置赋值
    if ((n % 2) == 1) {
        res[mid][mid] = count;
    }
    return res;
}