3.堆,栈,队列
知识框架:
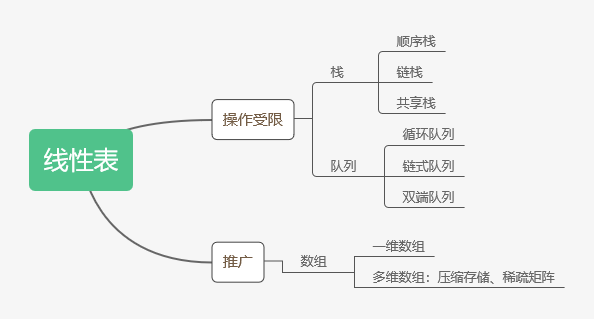
堆和栈的定义和区别(堆分配存储在下一章串和KMP算法中有所应用)
-
堆和栈都是一种数据项按序排列的数据结构。
-
堆像一棵倒过来的树:
1.堆是一种经过排序的树形数据结构,每个结点都有一个值。
2.通常我们所说的堆的数据结构,是指二叉堆。
3.堆的特点是根结点的值最小(或最大),且根结点的两个子树也是一个堆。
注意:由于堆的这个特性,常用来实现优先队列,堆的存取是随意,这就如同我们在图书馆的书架上取书,虽然书的摆放是有顺序的,但是我们想取任意一本时不必像栈一样,先取出前面所有的书,书架这种机制不同于箱子,我们可以直接取出我们想要的书。 -
栈像装数据的桶或箱子:
1.它是一种具有后进先出性质的数据结构,也就是说后存放的先取,先存放的后取。
2.这就如同我们要取出放在箱子里面底下的东西(放入的比较早的物体),我们首先要移开压在它上面的物体(放入的比较晚的物体)。
下面重点介绍栈和队列,堆留到下一节讨论
栈
栈及基本概念
- 栈(Stack): 是只允许在一端进行插入删除操作的线性表。首先栈是一种线性表,但限定这种线性表只能在一端进行插入删除操作。
- 栈顶(Top): 线性表允许进行插入删除的那一端。
- 栈底(Bottom):固定的,不允许进行插入删除的另一端。
- 空栈: 即不含任何元素的空表。
- 栈的数学性质:n个不同元素进栈,出栈元素不同排列的个数为1/n+1Cn 2n(卡特兰数),采用数学归纳法即可证明。
栈的基本操作
InitStack(&S):初始化一个空栈;
StackEmpty(S):判断一个栈是否为空,若栈S为空则返回true,否则返回false;
Push(&S,x):进栈,若栈S未满,则将x加入使之成为新栈项;
Pop($S,x):出栈,若栈未空,则弹出栈顶元素,并用x返回;
GetTop(S,&x);读栈顶元素,若栈非空,则用x返回栈顶元素;
DestroyStack(&S):销毁栈,并释放栈所占用的存储空间(“&”表示引用调用)
注意: 在解答算法题时,可直接使用这些基本操作函数。
栈的顺序存储结构
- 顺序栈的定义:采用顺序存储的栈称为顺序栈,它利用一组地址连续的存储单元存放自栈底向栈顶的数据元素,同时附设一个指针(top)用来指示当前栈顶元素的位置。
- 存储类型定义描述:
#define MaxSize 50
typedef struct{
ElemType data[MaxSize];
int top;
}SqStack;
栈顶指针:S.top,初始设置S.top = -1;栈顶元素:S.data[S.top]。
进栈操作:栈不满的时候,栈顶指针先加1,再送值到栈顶元素。
出栈操作:栈非空时,先取栈顶元素值,再将栈顶指针减1。
栈空条件:S.top == -1;栈满条件:S.top == MaxSize - 1;栈长:S.top+1。
注意: 由于顺序栈的入栈操作受到数组上界的约束,当栈的最大使用空间估计不足时,有可能发生栈上溢,此时应发送报错信息至用户,得到及时处理。
顺序栈的基本运算
1.初始化
void InitStack(SqStack &S)
{
S.top == -1;//初始化栈顶指针
}
2.判栈空
bool StackEmpty(SqStack S)
{
if(S.top == -1)
return true;
else
return false;
}
3.进栈
bool Push(SqStack &S,ElemType x)
{
if(S.top == MaxSize - 1)
return false;//栈满,报错
S.data[++S.top] = x;//指针先加1,再进栈
return true;
}
4.出栈
bool Pop(SqStack S,ElemType x)
{
if(S.top == -1)
return false;
x = S.data[S.top--];//先出栈,指针再减1
return true;
}
5.读栈顶元素
bool GetStackTop(SqStack S,ElemType &x)
{
if(S.top == -1)
return false;
x = S.data[S.top];//x记录栈顶元素
return true;
}
共享栈
利用栈底位置相对不变的特性,可让两个顺序栈共享一个一维数组空间,将两个栈的栈底分别设置在共享空间的两端,两个栈顶向共享空间中间部分进行延伸。如图:
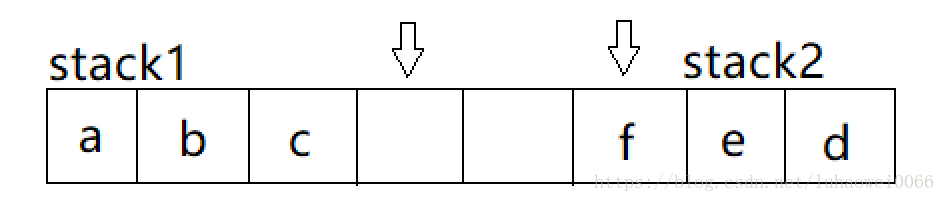
- 两个栈的栈顶指针都指向栈顶元素,top=-1时stack1为空,top'=MaxSize时stack2为空。仅当两个栈顶指针相邻(top'-top=1),判断栈满。当stack1进栈时,top先加1再赋值,stack2进栈时先减1再赋值;出栈则刚好相反。
栈的链式存储结构
-
采用链式存储的栈称为链栈,链栈的优点在于便于多个栈共享空间和提高效率,且不存在上溢的情况。通常采用单链表实现,并规定所有操作均在单链表的表头进行。这里规定链栈没有头结点,head指向栈顶元素。
![]()
-
栈的链式存储定义描述:
typedef struct LineStack{
ElemType data;
struct LineStack *next;
}*LineStack;
- 链栈元素入栈
例如,将元素 1、2、3、4 依次入栈,等价于将各元素采用头插法依次添加到链表中,每个数据元素的添加过程如图 :
![]()
//C语言实现
//链表中的节点结构
typedef struct lineStack{
int data;
struct lineStack * next;
}lineStack;
//stack为当前的链栈,a表示入栈元素
lineStack* push(lineStack * stack,int a){
//创建存储新元素的节点
lineStack * line=(lineStack*)malloc(sizeof(lineStack));
line->data=a;
//新节点与头节点建立逻辑关系
line->next=stack;
//更新头指针的指向
stack=line;
return stack;
}
- 链栈元素出栈
所示的链栈中,若要将元素 3 出栈,根据"先进后出"的原则,要先将元素 4 出栈,也就是从链表中摘除,然后元素 3 才能出栈,整个操作过程如图所示:
![]()
//栈顶元素出链栈的实现函数
lineStack * pop(lineStack * stack){
if (stack) {
//声明一个新指针指向栈顶节点
lineStack * p=stack;
//更新头指针
stack=stack->next;
printf("出栈元素:%d ",p->data);
if (stack) {
printf("新栈顶元素:%d\n",stack->data);
}else{
printf("栈已空\n");
}
free(p);
}else{
printf("栈内没有元素");
return stack;
}
return stack;
}
总结:不难发现,链栈实际上是通过头插法实现的,C语言代码展示如下:
#include <stdio.h>
#include <stdlib.h>
typedef struct lineStack{
int data;
struct lineStack * next;
}lineStack;
lineStack* push(lineStack * stack,int a){
lineStack * line=(lineStack*)malloc(sizeof(lineStack));
line->data=a;
line->next=stack;
stack=line;
return stack;
}
lineStack * pop(lineStack * stack){
if (stack) {
lineStack * p=stack;
stack=stack->next;
printf("弹栈元素:%d ",p->data);
if (stack) {
printf("栈顶元素:%d\n",stack->data);
}else{
printf("栈已空\n");
}
free(p);
}else{
printf("栈内没有元素");
return stack;
}
return stack;
}
int main() {
lineStack * stack=NULL;
stack=push(stack, 1);
stack=push(stack, 2);
stack=push(stack, 3);
stack=push(stack, 4);
stack=pop(stack);
stack=pop(stack);
stack=pop(stack);
stack=pop(stack);
stack=pop(stack);
return 0;
}
注意:事实上顺序栈应用更加广泛,所以重点应有以掌握顺序栈算法为主。
队列
队列的基本概念
- 队列(Queue): 简称队,也是一种操作受限的线性表,只允许在表的一端进行插入,而在表的另一端进行删除。向队列中插入元素称为入队或者进队;删除元素称为离队或者出队。特性本质为:先进先出(First In First Out,FIFO)。
- 队头(Front):允许删除的一端,又称为队首。
- 队尾(Rear):允许插入的一端。
- 空队列:不含任何元素的空表。
队列的基本操作
InitQueue(&Q):初始化队列;
QueueEmpty(Q):判队列为空,若队列Q为空则返回true,否则返回false;
EnQueue(&Q,x):入队,若队列Q未满,将x加入,使之成为新的队列;
DeQueue(&Q,x):出队,若队列非空,删除队头元素,并用x返回;
GetQueue(Q,&x):读队头元素,若队列非空,将队头元素赋值给x。
注意:由于栈和队列都属于操作受限的线性表,因此不是任何操作都可以作为其操作,比如无法随便读取栈或者队列中间某个元素。
队列的顺序存储结构
- 队列的顺序实现是指分配一块连续的存储单元存放队列中的元素,并附设两个指针:队头指针front指向队头元素和队尾指针rear指向队尾元素的下一个位置(当然也可以自定义)。
- 队列的顺序存储类型描述:
#define MaxSize 50
typedef struct{
ElemType data[MaxSize];
int front,rear;
}SqQueue;
初始状态:Q.front == Q.rear == 0;
进队操作:队不满时,先送值到队尾元素,再将队尾指针加1;
出队操作:队不空时,先取队头元素值,再将队头指针加1;
循环队列
将顺序队列臆造成一个环状的空间,即把存储队列元素的表视为一个环,称为循环队列。
- 初始时:Q.front = Q.rear=0;
- 队首指针进:Q.front=(Q.front+11)%MaxSize。
- 队尾指针进:Q.rear=(Q.rear+1)%MaxSize。
- 队列长度:(Q.rear-Q.front+MaxSize)%MaxSize。
- 队空条件和队满条件:
1.牺牲一个单元来区分队空和队满,入队时少用一个队列单元,这是一种较为普遍的做法,约定以“队头指针在队尾指针的下一位置作为队满的标志”。
此时队空条件为:Q.rear == Q.front;队满条件即(Q.rear+1)%MaxSize == Q.front。
2.存储结构定义类型中增设表示元素个数的数据成员(size)。这样,队空的条件为Q.size == 0;队满的条件为Q.size == MaxSize。这两种情况都有Q.front == Q.rear。
3.类型中增设tag数据成员来记录插入删除记录。设tag等于0时,因删除导致Q.front == Q.rear,则为队空;设tag等于1时,若因插入导致Q.front == Q.rear,则为队满。
以上三种方式均可以实现判断队空和队满的区分条件,一般采用第一种方法。
循环链表的操作实现
1.初始化:
void InitQueue(SqQueue &Q){
Q.rear =Q.front = 0;
}
2.判队空:
bool isEmpty(SqQueue Q)
{
if(Q.rear == Q.front)
return true;
else return false;
3.入队:
bool EnQueue(SqQueue &Q,ElemType x)
{
if((Q.rear + MaxSize) == Q.front)
return false;//队满,出错
Q.data[Q.rear] = x;
Q.rear = (Q.rear + 1)%MaxSize;//队尾指针加1
return true;
}
4.出队:
bool DeQueue(SqQueue &Q,ElemType &x)
{
if(Q.rear == Q.front)
return false;
x = Q.data[Q.front];
Q.front = (Q.front + 1 )%MaxSzie;
return true;
}
队列的链式存储结构
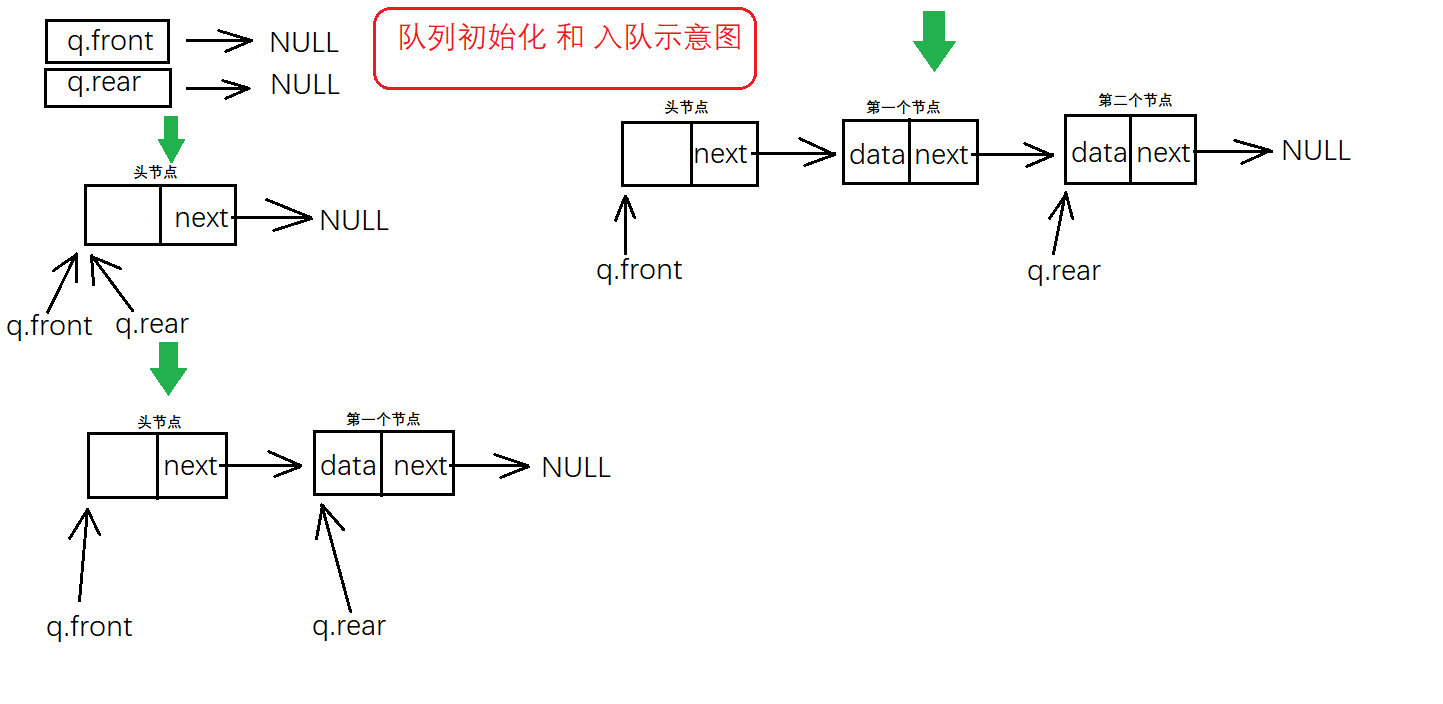
- 队列的链式表示称为链队列;实际上是一个同时带有队头指针和队尾指针的单链表。头指针指向对头结点,尾指针指向队尾结点,即单链表最后一个结点。
- 链队列的存储结构定义描述为:
typedef struct
{
ElemType data;
struct LinkNode *next;
}LinkNode;
typedef struct{
LinkNode *front,*rear;
}LinkQueue;
链式队列的基本操作
1.初始化:
void InitQueue(LinkQueue Q){
Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode));
Q.front->next = NULL;
}
2.判队空:
bool isEmpty(LinkQueue Q){
if (Q.front == Q.rear)
return true;
else return false;
}
3、入队:
void EnQueue(LinkQueue &Q,ElemType x)
{
LinkNode *s=(LinkNode*)malloc(sizeof(LinkNode));
s->data = x;
s->next = NULL;
Q.rear->next = s;
Q.rear = s;//更新尾指针
}
4.入队:
bool DeQueue(LinkQueue &Q,ElemType x)
{
if(Q.rear == Q.front)
return false;
LinkNode *p = Q.front->next;
x = p->data;
Q.front->next = p->next;
if(Q.rear == p)
Q.rear = Q.front;
free(p);
return true;
}
双端队列
- 双端队列是指允许两端可以进行入队和出队操作的队列。逻辑结构仍然是线性结构。
蛮简单的。略~



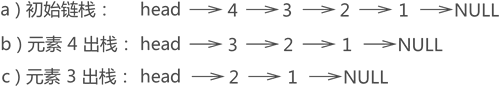

 浙公网安备 33010602011771号
浙公网安备 33010602011771号