2.线性表

线性表

1.线性表的类型定义

• 线性表（linear_list）是最常用且最简单的一种数据结构。简言之，一个线性表是n个数据元素的有限序列。通常记为（a1,a2,a3...an）。
  在稍复杂的线性表里，一个数据元素可以由若干数据项构成，在这种情况下，常把数据元素称为记录，含有大量记录的线性表称为文件。
• 线性表中元素的个数（n,n>=0）定义为线性表的长度（表长），n=0时称为空表。ai是第i个数据元素，称i为数据元素ai在线性表中的位序，表的起始位置称为表头，表的结束位置称为表尾。

抽象数据类型线性表定义如下：

ADT List{
数据对象： D={ai|ai∈ElemSet, i=l, 2, …,n,n>=0}
数据关系：R=(<ai-1,ai>|ai-1,ai∈D, i=2,…,n}
基本操作：
InitList (&L)
操作结果：构造一个空的线性表L。
DestroyList(&L)
初始条件：线性表L已存在。
操作结果：销毁线性表L。
ClearList (&L)
初始条件：线性表L已存在。
操作结果：将L重置为空表。
ListEmpty(L)
初始条件：线性表L已存在。
操作结果：若L为空表，则返回true, 否则返回false。
ListLength(L)
初始条件：线性表L已存在。
操作结果：返回L中数据元素个数。
GetElem(L,i,&e)
初始条件：线性表L巳存在，且1<=i<=ListLength(L)。
操作结果：用e返回L中第1个数据元素的值。
LocateElem(L,e)
初始条件：线性表L已存在。
操作结果：返回L中第1个 值与e相同的元素在L中的位置。若这样的数据元素不存在，则返回值为0。
PriorElem(L,cur_e,&pre_e)
初始条件：线性表L已存在。
操作结果：若cur_e是L的数据元素，且不是第一个，则用pre_e返回其前驱，否则操作失败，pre_e无定义。
NextElem(L,cur_e,&next_e)
初始条件：线性表L已存在。
操作结果：若cur_e是L的数据元素，且不是最后一个，则用next_e返回其后继，否则操作失败，next_e无定义。
ListInsert(&L,i,e)
初始条件：线性表L已存在，且1<=i<=ListLength (L) +l。
操作结果：在 L中第i个位置之前插入新的数据元素 e, L的长度加1。
ListDelete(&L,i,&e)
初始条件：线性表L已存在且非空，且1<=i<=ListLength(L)。
操作结果：删除L的第1个数据元素，L的长度减1。
TraverseList(L)
初始条件：线性表L已存在。
操作结果：对线性表L进行遍历，在遍历过程中对 L的每个结点访问一次。
} ADT List

2.线性表的顺序表示和实现

• 线性表的顺序表示指用一组地址连续的存储单元依次存储线性表的数据元素。
  
• 主要操作的实现：
  1.初始化：

List MakeEmpty()
{  List PtrL;
   PtrL = (List)malloc(sizeof(struct LNode));
   PtrL->Last = -1;//由于Last指向最后一个元素，设为-1则表示为空表
   return PtrL;
}

2.查找：

int Find(Elemtype X,List PtrL)
{
  int i = 0;
  while(i <= PtrL->Last && PtrL->Data[i] != X)
  i++;
  if(i > PtrL->Last)
  return -1;//未找到符合条件的元素
  else return i;
}

查找成功的平均比较次数为（n+1）/2,平均时间性能为O（n）。
3.插入（将X插入到第i个元素原本的位置，即在第n个元素到第i个元素都向后移动一个位置）

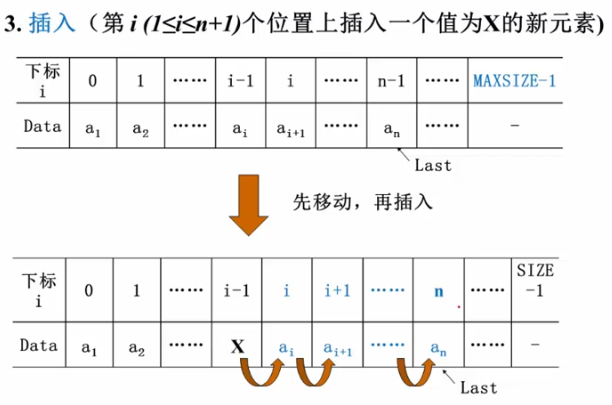
void Insert(Elemtype X,int i,List PtrL)
{ int j;
  if(PtrL->Last == MAXSIZE-1)
  printf("表满，无法插入！！！");
  return；
  if(i<1||i>PtrL->Last+2)
  printf("插入位置不合法！！！");
  return；
  for(j = PtrL->Last;j >= i-1;j--)
  PtrL->Data[j+1] = PtrL->Data[j];
  PtrL->Data[i-1] = X;
  PtrL->Last++;
  return;
}

4.删除（删除第i个元素，即第i+1个元素到最后一个元素前移一位，并更新PtrL->Last）

void Delete(List PtrL,int i)
{       int j;
	if(i <1 || i > PtrL->Last+1)
		printf("删除位置非法！");
                return;
	for(j = i;j <= PtrL->Last;j++)
	{
		PtrL->Data[j-1] = PtrL->Data[j];
        }
		PtrL->Last--;
                return;
}

其平均移动次数为(n-1)/2,平均时间性能为O（n）。

• 顺序表的优缺点：
  优点：

1. 节省存储空间；
2. 对线性表中第i个元素的操作易于实现；
3. 容易查找一个元素的前驱和后继。
   缺点：
4. 插入和删除需要移动数据；
5. 建立空表时，较难确定所需要的存储空间。

3.线性表的链式表示和实现

• 线性表的链式存储特点是用一组任意的存储单元存储线性表的数据元素。（这组存储单元可以连续也可以不连续）
  不要求逻辑上相邻的两个元素在物理存储结构上也相邻，通过“链”建立起数据元素之间的逻辑关系。
• 对于每个数据元素ai来说，除了存储本身信息之外，还需要存储一个指示其直接后继的信息（即直接后继的位置）。这两部分信息组成数据元素ai的存储映像，称为结点。包括两个域：存储数据元素信息的域称为数据域；存储直接后继存储位置的域称为指针域。指针域中存储的信息称为指针或者链。n个结点（ai的存储映像）链结成一个链表，即为线性表的链式存储结构。
• 由于此链表的每个结点中只包含一个指针域，故又称线性链表或者单链表。
  
  注意：在链表里，插入删除不需要移动数据元素，只需要修改“链”。
  形式定义如下：
  
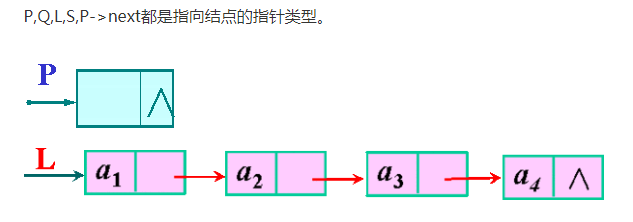
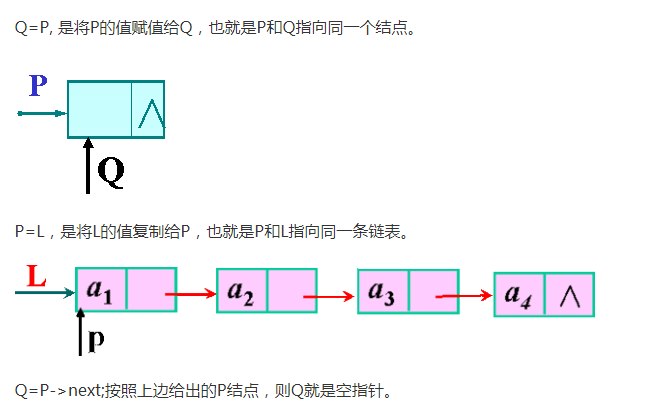
  拓展：p=p->next表示修改指针p的位置,把p指向原来的下一个节点。关于P=Q和P->next=L;p=p->next;如图所示：
  
  
• 主要操作的实现：
• 初始化

//初始化：
List initLink()
{
	List p = NULL;//创建头指针
	List PtrL = (List)malloc(sizeof(struct LNode));//创建首元结点
	PtrL->Data = 1;
	PtrL->Next = NULL;//初始化首元结点
	p = PtrL;
	for(int i = 2; i <= 5; i++)
	{
		List x = (List)malloc(sizeof(struct LNode));//创建一个新的结点复用
		x->Data = i;
		x->next=NULL;//初始化
		PtrL->Next = x;//建立结点间逻辑关系
		PtrL = PtrL->Next;//更新结点
	}
	return p;//通过头指针访问整个链表即可
}

1. 求表长

int Length(List PtrL)
{
	List p = PtrL;//p指向表的第一个节点
	int i = 0;//作为计数器
	while(p)
	{
		p = p->Next;
		i++;//当前p指向的是第i+1个结点
	}
	return i;
}

2. 查找
   （1）按序号查找，即查找第K个元素。

int FindKth(int K,List PtrL)
{
	List p = PtrL;
	int i = 1;
	while(p != NULL && i < K)
	{
		p = p->Next;
		i++;
	}
	if(i == K)
		return p;
	else
		return NULL;
}

（2）按值查找

int Find(Elemtype X,List PtrL)
{
	List p = PtrL;
	while(p != NULL && p->Data != X)
	{
		p = p->Next;
	}
	return p;
}

3. 插入

int Insert(int i,List PtrL,Elemtype X)
{
	List p,s;//p指的是第（i-1)个结点，s指要插入的结点，其数据域应该为X
	if(i == 1)//特殊情况：该结点插入该单链表表头，故单独处理
	{
		s = (List)malloc(sizeof(Struct LNode));//申请，填装结点
		s->Next = PtrL;
		s->Data = X;
		return s;//返回新的表头指针
	}
	p = FindKth(i-1,PtrL);//确定p的位置，即第i-1个结点
	if(p == NULL)
	{
		printf("第i-1个结点不存在，无法插入！");
		return NULL;
	}
	else 
	{
		s = (List)malloc(sizeof(Struct LNode));//申请，填装结点
		s->Next = p->Next;//新结点插入到第(i-1)个结点后面
		s->Data = X;
		p->Next = s;
		return PtrL;
	}
}

4. 删除

List Delete(int i,List ptrL)
{
	List p,s;
	if(i == 1)//特殊情况：如果要删除的结点为第一个结点
	{
		s = PtrL;//s指向第一个结点
		if(PtrL !=NULL)
			PtrL = PtrL->Next;//从链表中删除
		else
			return NULL;
		free(s);//释放被删除的结点
		return PtrL;
	}
	p = FindKth(i-1,PtrL);//查找第（i-1)个结点
	if(p == NULL){
		printf("第%d个结点为空"，i-1);
	    return NULL;
	}
	else if(p->Next == NULL){
		printf("第%d个结点为空"，i);
	    return NULL;
	}
	else
	{
		s = p->Next;//s指向第i个结点
		P->Next = s->Next;//从链表中删除
		free(s);//释放被删除的结点
		return PtrL;
	}
}

当然不难看出，不管是插入还是删除，都需要先找到第i-1个结点，故时间复杂度均为O（n）。
附：执行 p = (List)malloc(sizeof(struct LNode))作用是由系统生成一个LNode型的变量，同时该结点的起始位置赋给指针变量p;反之，执行free(p),系统将回收LNode型结点。

循环链表

• 循环链表（circle linked list）是另外一种形式的链式存储结构。循环链表的结构和单链表结构一样，不过对于单链表，每个结点只存储了向后的指针，到了尾标志就停止了向后链的操作，这样知道某个结点却无法找到它的前驱结点。将单链表中的终端点的指针由空指针改为指向头结点，就使整个单链表形成一个环，这种头尾相接的单链表称为循环单链表，简称循环链表。
  特点：表中最后一个结点的指针域指向头结点，整个链表形成一个环。
  
• 循环链表的操作与线性链表基本一致，差别仅在于算法中的循环条件不是p或者p->Next是否为空，而是它们是否等于头指针。
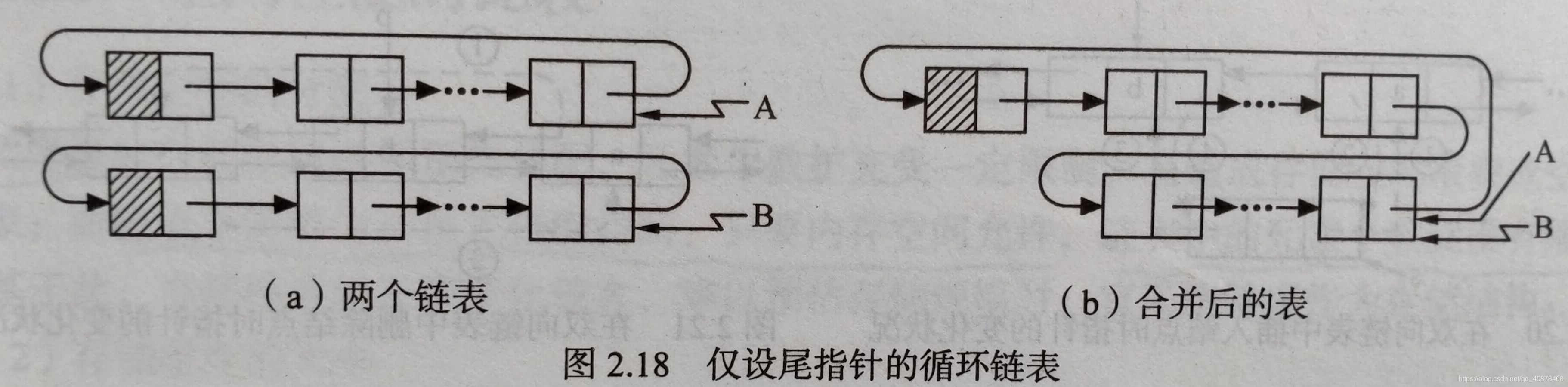
• 在某些情况下，若在循环链表中设立尾指针而不设头指针，可使一些操作简化。当线性表以下图的循环链表作存储结构时，这个操作仅需改变两个指针值即可，主要语句段如下：p=B->next->next; B->next=A->next; A->next=p;上述操作的时间复杂度为O（1），合并后的表如下图。
  

双向链表

• 以上讨论的链式存储结构的结点中只有一个指示直接后继的指针域，由此，从某个结点出发只能顺指针向后寻查其他结点。若要寻查结点的直接前驱，则必须从表头指针出发。
• 在单链表中，查找直接后继点的执行时间为O（1），而查找直接前驱的执行时间为O（n）。为克服单链表折中单向性的缺点，可利用双向链表（Double Linked List）。
• 特点：在双向链表的结点中有两个指针域，一个指向直接后继，另一个指向直接前驱。
  双向链表的存储结构：

 - - - - -双向链表的存储结构- - - - -
    typedef struct DuLNode
    {
       ElemType data;               //数据域
       struct DuLNode *prior;       //直接前驱
       struct DuLNode *next;        //直接后继
    }DuLNode,*DuLinkList;

如图所示：

双向链表也可以有循环表。在双向链表中，若d为指向表中某一结点的指针（即d为DuLinkList型变量），则显然有 d->next->prior=d->prior->next=d。
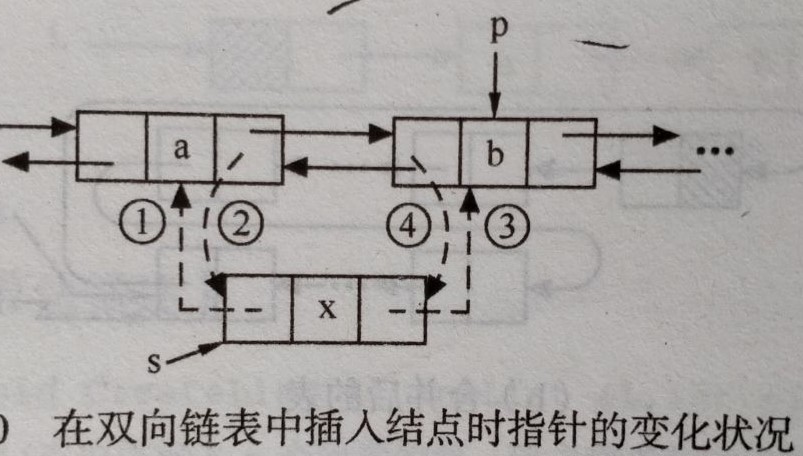
*在双向链表中，有些操作（如ListLength、GetElem和LocateElem等）仅需涉及一个方向的指针，则它们的算法描述和线性链表的操作相同，但在插入、删除时有很大的不同，在双向链表中需同时修改两个方向上的指针。在插入结点时需要修改四个指针，在删除结点时需要修改两个指针。两者的时间复杂度均为O（n）。

• 主要操作的实现

1. 插入
   

    Status ListInsert_DuL(DuLinkList &L,int i,ElemType e)
    {//在带头结点的双向链表L中第i个位置之前插入元素e
       if(!(p=GetElem_DuL(L,i)))            //在L中确定第i个元素的位置指针p
         return ERROR;                      //p为NULL时，第i个元素不存在
       s=new DulNode;                       //生成新结点*s
       s->data=e;                           //将结点*s数据域置为e
       s->prior=p->prior;                   //将结点*s插入L中，对应1
       p->prior->next=s;                    //对应2
       s->next=p;                           //对应3
       p->prior=s;                          //对应4
       return OK;
    }

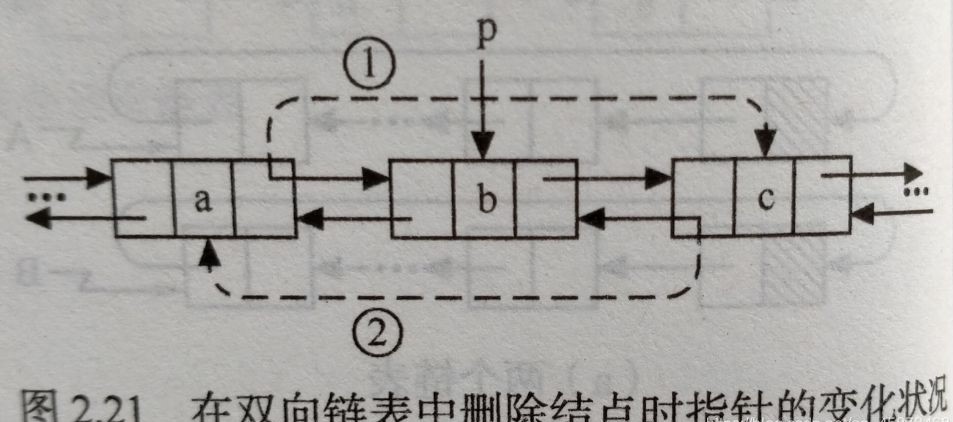
2. 删除
   

    Status ListDelete_DuL(DuLinkList &L,int i)
    {//删除带头结点的双向链表L中的第i个元素
       if(!(p=GetElem_DuL(L,i)))                 //在L中确定第i个元素的位置指针p
          return ERROR;                          //p为NULL时，第i个元素不存在
       p->prior->next=p->next;                   //修改被删结点的前驱结点的后继指针，对应1
       p->next->prior=p->prior;                  //修改被删结点的后继结点的前驱指针，对应2
       delete p;                                 //释放被删结点的空间
       return OK;
    }

单链表、循环链表和双向链表的比较

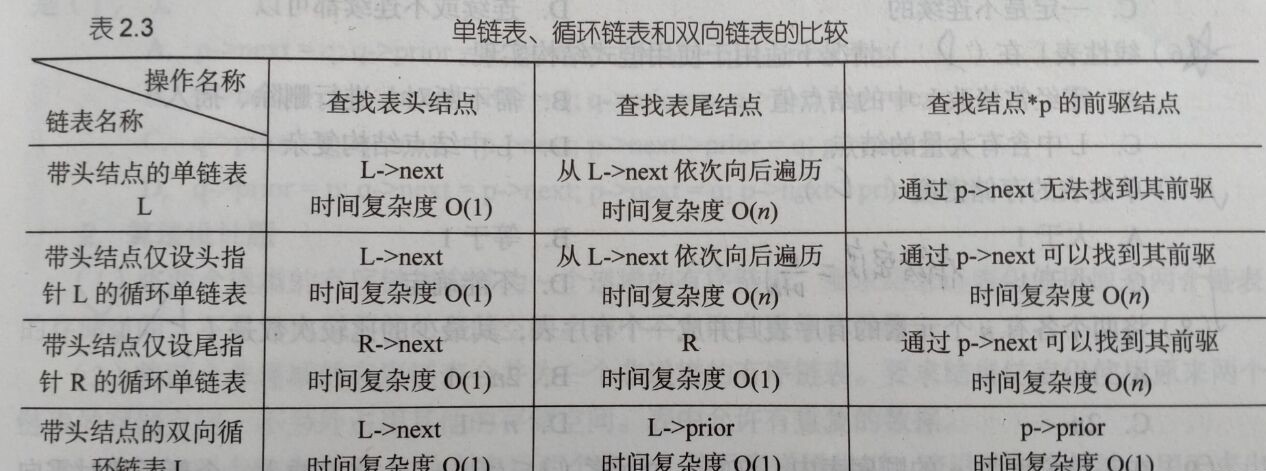
顺序表和链表进行比较

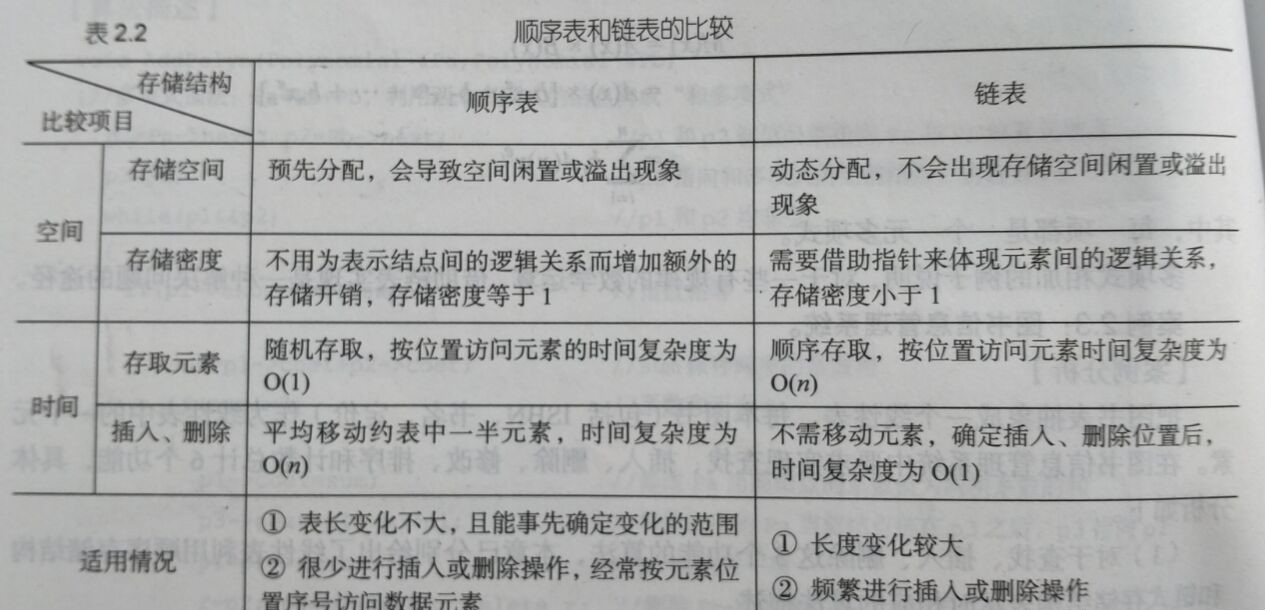
一元多项式的表示及相加

方法1.顺序存储结构直接表示

方法2.顺序存储结构表示非零项

方法3.链式结构存储非零项