费马定理

极值点导数为零。
罗尔中值定理
区间端点相等,导数为零。
如果 R 上的函数 f(x) 满足以下条件:(1)在闭区间 [a,b] 上连续,(2)在开区间 (a,b) 内可导,(3)f(a)=f(b),则至少存在一个 ξ∈(a,b),使得 f’(ξ)=0。
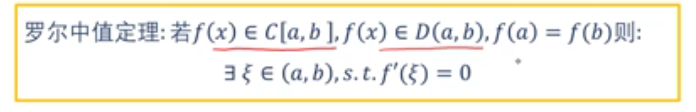
零点存在定理
假设函数f(x)在闭区间[a, b]上连续,且函数值f(a)与f(b)异号(即,一为正一为负)。则在开区间(a, b)上必定存在至少一个c,使得f© = 0。

介值定理

介值定理如果A=B,则开区间(a,b)内可能取不到端点值A,B
拉格朗日中值定理
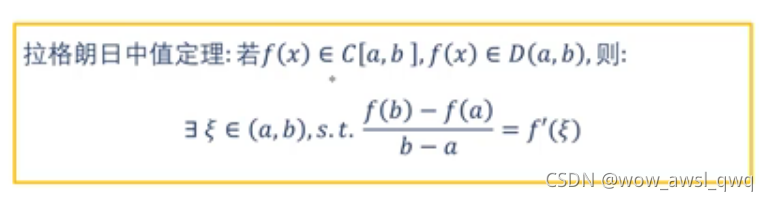
达布定理

积分中值定理

泰勒中值定理

