欧几里得算法 扩展欧几里得算法 更相减损术（辗转相减法 ）代码实现

欧几里得算法

原理：gcd(a,b)=gcd(b,a%b)

	static int gcd(int a,int b)
	{
		return (b==0)?a:gcd(b,a%b);
	}

原理：gcd(a,b)=gcd(b,a-b)

	static int gcd1(int a,int b)
	{
		if(a<b)
		{
			int t=a;
			a=b;
			b=t;
		}
		return (b==0)?a:gcd1(b,a-b);
	}

辗转相减法的应用

用来求同幂p时,指数的最大公约数对应的指数值
原理：

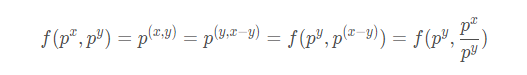
//用来求同幂p时,指数的最大公约数对应的指数值，结果不一定就是a和b的最大公约数
//比如b=1时，相当于指数为0，a对应的指数和0的最大公约数是本身，因此结果还是a,而不是1
	static int gcd_sub(int a,int b)
	{
		if(a<b)
		{
			int t=a;
			a=b;
			b=t;
		}
		return (b==1)?a:gcd_sum(b,a/b);
	}

扩展欧几里得算法

	static long gcd(long a,long b,long []x,long []y)
	{
		if(b==0)
		{
			x[0]=1;y[0]=0;
			return a;
		}
		long d=gcd(b,a%b,y,x);
		y[0]-=a/b*x[0];
		return d;
	}

通解的形式

x=x0+kb/d		即系数为：b/d
y=y0+ka/d		即系数为：a/d

求x的最小正值：设t=b/d为x对应的系数，则结果为： (x%t+t)%t