<div id="page_begin_html">
<style>
back-top {
position: fixed;
bottom: 5px;
right: 10px;
z-index: 99;
}
back-top span {
width: 50px;
height: 64px;
display: block;
background:url(http://images.cnblogs.com/cnblogs_com/shwee/1218109/o_toTop.bmp) no-repeat center center;
}
back-top a
|
|
</div>
</div>
<div id="cnblogs_post_body" class="blogpost-body blogpost-body-html"><a rel="nofollow" name="_labelTop"></a><div id="navCategory"><p style="font-size:18px"><b>阅读目录(Content)</b></p><ul class="first_class_ul"><li><a rel="nofollow" href="#_label0">浅谈范数正则化</a></li><ul class="second_class_ul"><li><a rel="nofollow" href="#_lab2_0_0">1. 向量范数与矩阵范数</a></li><li><a rel="nofollow" href="#_lab2_0_1">2. 为什么要添加正则项?</a></li><li><a rel="nofollow" href="#_lab2_0_2">3. <span class="MathJax_Preview" style="color: inherit;"></span><span class="MathJax" id="MathJax-Element-1-Frame" tabindex="0" style="position: relative;" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>L</mi><mn>0</mn></msub></math>" role="presentation"><nobr aria-hidden="true"><span class="math" id="MathJax-Span-1" style="width: 1.47em; display: inline-block;"><span style="display: inline-block; position: relative; width: 1.133em; height: 0px; font-size: 125%;"><span style="position: absolute; clip: rect(1.45em, 1001.13em, 2.699em, -1000em); top: -2.333em; left: 0em;"><span class="mrow" id="MathJax-Span-2"><span class="msubsup" id="MathJax-Span-3"><span style="display: inline-block; position: relative; width: 1.11em; height: 0px;"><span style="position: absolute; clip: rect(3.117em, 1000.65em, 4.2em, -1000em); top: -4em; left: 0em;"><span class="mi" id="MathJax-Span-4" style="font-family: MathJax_Math; font-style: italic;">L</span><span style="display: inline-block; width: 0px; height: 4em;"></span></span><span style="position: absolute; top: -3.85em; left: 0.681em;"><span class="mn" id="MathJax-Span-5" style="font-size: 70.7%; font-family: MathJax_Main;">0</span><span style="display: inline-block; width: 0px; height: 4em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 2.333em;"></span></span></span><span style="display: inline-block; overflow: hidden; vertical-align: -0.29em; border-left: 0px solid; width: 0px; height: 1.227em;"></span></span></nobr><span class="MJX_Assistive_MathML" role="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>L</mi><mn>0</mn></msub></math></span></span><script type="math/tex" id="MathJax-Element-1">L_0</script>范数</a></li><li><a rel="nofollow" href="#_lab2_0_3">4. <span class="MathJax_Preview" style="color: inherit;"></span><span class="MathJax" id="MathJax-Element-2-Frame" tabindex="0" style="position: relative;" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>L</mi><mn>1</mn></msub></math>" role="presentation"><nobr aria-hidden="true"><span class="math" id="MathJax-Span-6" style="width: 1.47em; display: inline-block;"><span style="display: inline-block; position: relative; width: 1.133em; height: 0px; font-size: 125%;"><span style="position: absolute; clip: rect(1.45em, 1001.13em, 2.683em, -1000em); top: -2.333em; left: 0em;"><span class="mrow" id="MathJax-Span-7"><span class="msubsup" id="MathJax-Span-8"><span style="display: inline-block; position: relative; width: 1.11em; height: 0px;"><span style="position: absolute; clip: rect(3.117em, 1000.65em, 4.2em, -1000em); top: -4em; left: 0em;"><span class="mi" id="MathJax-Span-9" style="font-family: MathJax_Math; font-style: italic;">L</span><span style="display: inline-block; width: 0px; height: 4em;"></span></span><span style="position: absolute; top: -3.85em; left: 0.681em;"><span class="mn" id="MathJax-Span-10" style="font-size: 70.7%; font-family: MathJax_Main;">1</span><span style="display: inline-block; width: 0px; height: 4em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 2.333em;"></span></span></span><span style="display: inline-block; overflow: hidden; vertical-align: -0.271em; border-left: 0px solid; width: 0px; height: 1.208em;"></span></span></nobr><span class="MJX_Assistive_MathML" role="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>L</mi><mn>1</mn></msub></math></span></span><script type="math/tex" id="MathJax-Element-2">L_1</script>范数</a></li><li><a rel="nofollow" href="#_lab2_0_4">5. <span class="MathJax_Preview" style="color: inherit;"></span><span class="MathJax" id="MathJax-Element-3-Frame" tabindex="0" style="position: relative;" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>L</mi><mn>2</mn></msub></math>" role="presentation"><nobr aria-hidden="true"><span class="math" id="MathJax-Span-11" style="width: 1.47em; display: inline-block;"><span style="display: inline-block; position: relative; width: 1.133em; height: 0px; font-size: 125%;"><span style="position: absolute; clip: rect(1.45em, 1001.13em, 2.683em, -1000em); top: -2.333em; left: 0em;"><span class="mrow" id="MathJax-Span-12"><span class="msubsup" id="MathJax-Span-13"><span style="display: inline-block; position: relative; width: 1.11em; height: 0px;"><span style="position: absolute; clip: rect(3.117em, 1000.65em, 4.2em, -1000em); top: -4em; left: 0em;"><span class="mi" id="MathJax-Span-14" style="font-family: MathJax_Math; font-style: italic;">L</span><span style="display: inline-block; width: 0px; height: 4em;"></span></span><span style="position: absolute; top: -3.85em; left: 0.681em;"><span class="mn" id="MathJax-Span-15" style="font-size: 70.7%; font-family: MathJax_Main;">2</span><span style="display: inline-block; width: 0px; height: 4em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 2.333em;"></span></span></span><span style="display: inline-block; overflow: hidden; vertical-align: -0.271em; border-left: 0px solid; width: 0px; height: 1.208em;"></span></span></nobr><span class="MJX_Assistive_MathML" role="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>L</mi><mn>2</mn></msub></math></span></span><script type="math/tex" id="MathJax-Element-3">L_2</script>范数</a></li><li><a rel="nofollow" href="#_lab2_0_5">6. <span class="MathJax_Preview" style="color: inherit;"></span><span class="MathJax" id="MathJax-Element-4-Frame" tabindex="0" style="position: relative;" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>L</mi><mn>1</mn></msub></math>" role="presentation"><nobr aria-hidden="true"><span class="math" id="MathJax-Span-16" style="width: 1.47em; display: inline-block;"><span style="display: inline-block; position: relative; width: 1.133em; height: 0px; font-size: 125%;"><span style="position: absolute; clip: rect(1.45em, 1001.13em, 2.683em, -1000em); top: -2.333em; left: 0em;"><span class="mrow" id="MathJax-Span-17"><span class="msubsup" id="MathJax-Span-18"><span style="display: inline-block; position: relative; width: 1.11em; height: 0px;"><span style="position: absolute; clip: rect(3.117em, 1000.65em, 4.2em, -1000em); top: -4em; left: 0em;"><span class="mi" id="MathJax-Span-19" style="font-family: MathJax_Math; font-style: italic;">L</span><span style="display: inline-block; width: 0px; height: 4em;"></span></span><span style="position: absolute; top: -3.85em; left: 0.681em;"><span class="mn" id="MathJax-Span-20" style="font-size: 70.7%; font-family: MathJax_Main;">1</span><span style="display: inline-block; width: 0px; height: 4em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 2.333em;"></span></span></span><span style="display: inline-block; overflow: hidden; vertical-align: -0.271em; border-left: 0px solid; width: 0px; height: 1.208em;"></span></span></nobr><span class="MJX_Assistive_MathML" role="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>L</mi><mn>1</mn></msub></math></span></span><script type="math/tex" id="MathJax-Element-4">L_1</script>范数与<span class="MathJax_Preview" style="color: inherit;"></span><span class="MathJax" id="MathJax-Element-5-Frame" tabindex="0" style="position: relative;" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>L</mi><mn>2</mn></msub></math>" role="presentation"><nobr aria-hidden="true"><span class="math" id="MathJax-Span-21" style="width: 1.47em; display: inline-block;"><span style="display: inline-block; position: relative; width: 1.133em; height: 0px; font-size: 125%;"><span style="position: absolute; clip: rect(1.45em, 1001.13em, 2.683em, -1000em); top: -2.333em; left: 0em;"><span class="mrow" id="MathJax-Span-22"><span class="msubsup" id="MathJax-Span-23"><span style="display: inline-block; position: relative; width: 1.11em; height: 0px;"><span style="position: absolute; clip: rect(3.117em, 1000.65em, 4.2em, -1000em); top: -4em; left: 0em;"><span class="mi" id="MathJax-Span-24" style="font-family: MathJax_Math; font-style: italic;">L</span><span style="display: inline-block; width: 0px; height: 4em;"></span></span><span style="position: absolute; top: -3.85em; left: 0.681em;"><span class="mn" id="MathJax-Span-25" style="font-size: 70.7%; font-family: MathJax_Main;">2</span><span style="display: inline-block; width: 0px; height: 4em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 2.333em;"></span></span></span><span style="display: inline-block; overflow: hidden; vertical-align: -0.271em; border-left: 0px solid; width: 0px; height: 1.208em;"></span></span></nobr><span class="MJX_Assistive_MathML" role="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>L</mi><mn>2</mn></msub></math></span></span><script type="math/tex" id="MathJax-Element-5">L_2</script>范数作为正则项的区别</a></li><li><a rel="nofollow" href="#_lab2_0_6">7. 用概率解释传统线性回归模型</a></li><li><a rel="nofollow" href="#_lab2_0_7">8. <span class="MathJax_Preview" style="color: inherit;"></span><span class="MathJax" id="MathJax-Element-6-Frame" tabindex="0" style="position: relative;" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>L</mi><mn>2</mn></msub></math>" role="presentation"><nobr aria-hidden="true"><span class="math" id="MathJax-Span-26" style="width: 1.47em; display: inline-block;"><span style="display: inline-block; position: relative; width: 1.133em; height: 0px; font-size: 125%;"><span style="position: absolute; clip: rect(1.45em, 1001.13em, 2.683em, -1000em); top: -2.333em; left: 0em;"><span class="mrow" id="MathJax-Span-27"><span class="msubsup" id="MathJax-Span-28"><span style="display: inline-block; position: relative; width: 1.11em; height: 0px;"><span style="position: absolute; clip: rect(3.117em, 1000.65em, 4.2em, -1000em); top: -4em; left: 0em;"><span class="mi" id="MathJax-Span-29" style="font-family: MathJax_Math; font-style: italic;">L</span><span style="display: inline-block; width: 0px; height: 4em;"></span></span><span style="position: absolute; top: -3.85em; left: 0.681em;"><span class="mn" id="MathJax-Span-30" style="font-size: 70.7%; font-family: MathJax_Main;">2</span><span style="display: inline-block; width: 0px; height: 4em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 2.333em;"></span></span></span><span style="display: inline-block; overflow: hidden; vertical-align: -0.271em; border-left: 0px solid; width: 0px; height: 1.208em;"></span></span></nobr><span class="MJX_Assistive_MathML" role="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>L</mi><mn>2</mn></msub></math></span></span><script type="math/tex" id="MathJax-Element-6">L_2</script>范等价于Gauss先验</a></li><li><a rel="nofollow" href="#_lab2_0_8">9. <span class="MathJax_Preview" style="color: inherit;"></span><span class="MathJax" id="MathJax-Element-7-Frame" tabindex="0" style="position: relative;" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>L</mi><mn>1</mn></msub></math>" role="presentation"><nobr aria-hidden="true"><span class="math" id="MathJax-Span-31" style="width: 1.47em; display: inline-block;"><span style="display: inline-block; position: relative; width: 1.133em; height: 0px; font-size: 125%;"><span style="position: absolute; clip: rect(1.45em, 1001.13em, 2.683em, -1000em); top: -2.333em; left: 0em;"><span class="mrow" id="MathJax-Span-32"><span class="msubsup" id="MathJax-Span-33"><span style="display: inline-block; position: relative; width: 1.11em; height: 0px;"><span style="position: absolute; clip: rect(3.117em, 1000.65em, 4.2em, -1000em); top: -4em; left: 0em;"><span class="mi" id="MathJax-Span-34" style="font-family: MathJax_Math; font-style: italic;">L</span><span style="display: inline-block; width: 0px; height: 4em;"></span></span><span style="position: absolute; top: -3.85em; left: 0.681em;"><span class="mn" id="MathJax-Span-35" style="font-size: 70.7%; font-family: MathJax_Main;">1</span><span style="display: inline-block; width: 0px; height: 4em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 2.333em;"></span></span></span><span style="display: inline-block; overflow: hidden; vertical-align: -0.271em; border-left: 0px solid; width: 0px; height: 1.208em;"></span></span></nobr><span class="MJX_Assistive_MathML" role="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>L</mi><mn>1</mn></msub></math></span></span><script type="math/tex" id="MathJax-Element-7">L_1</script>范数等价于Laplace先验</a></li><li><a rel="nofollow" href="#_lab2_0_9">10. 矩阵的<span class="MathJax_Preview" style="color: inherit;"></span><span class="MathJax" id="MathJax-Element-8-Frame" tabindex="0" style="position: relative;" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>L</mi><mrow class="MJX-TeXAtom-ORD"><mn>2</mn><mo>,</mo><mn>1</mn></mrow></msub></math>" role="presentation"><nobr aria-hidden="true"><span class="math" id="MathJax-Span-36" style="width: 2.137em; display: inline-block;"><span style="display: inline-block; position: relative; width: 1.667em; height: 0px; font-size: 125%;"><span style="position: absolute; clip: rect(1.45em, 1001.67em, 2.821em, -1000em); top: -2.333em; left: 0em;"><span class="mrow" id="MathJax-Span-37"><span class="msubsup" id="MathJax-Span-38"><span style="display: inline-block; position: relative; width: 1.66em; height: 0px;"><span style="position: absolute; clip: rect(3.117em, 1000.65em, 4.2em, -1000em); top: -4em; left: 0em;"><span class="mi" id="MathJax-Span-39" style="font-family: MathJax_Math; font-style: italic;">L</span><span style="display: inline-block; width: 0px; height: 4em;"></span></span><span style="position: absolute; top: -3.85em; left: 0.681em;"><span class="texatom" id="MathJax-Span-40"><span class="mrow" id="MathJax-Span-41"><span class="mn" id="MathJax-Span-42" style="font-size: 70.7%; font-family: MathJax_Main;">2</span><span class="mo" id="MathJax-Span-43" style="font-size: 70.7%; font-family: MathJax_Main;">,</span><span class="mn" id="MathJax-Span-44" style="font-size: 70.7%; font-family: MathJax_Main;">1</span></span></span><span style="display: inline-block; width: 0px; height: 4em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 2.333em;"></span></span></span><span style="display: inline-block; overflow: hidden; vertical-align: -0.442em; border-left: 0px solid; width: 0px; height: 1.379em;"></span></span></nobr><span class="MJX_Assistive_MathML" role="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>L</mi><mrow class="MJX-TeXAtom-ORD"><mn>2</mn><mo>,</mo><mn>1</mn></mrow></msub></math></span></span><script type="math/tex" id="MathJax-Element-8">L_{2, 1}</script>范数及<span class="MathJax_Preview" style="color: inherit;"></span><span class="MathJax" id="MathJax-Element-9-Frame" tabindex="0" style="position: relative;" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>L</mi><mrow class="MJX-TeXAtom-ORD"><mi>p</mi><mo>,</mo><mi>q</mi></mrow></msub></math>" role="presentation"><nobr aria-hidden="true"><span class="math" id="MathJax-Span-45" style="width: 2.137em; display: inline-block;"><span style="display: inline-block; position: relative; width: 1.667em; height: 0px; font-size: 125%;"><span style="position: absolute; clip: rect(1.45em, 1001.67em, 2.821em, -1000em); top: -2.333em; left: 0em;"><span class="mrow" id="MathJax-Span-46"><span class="msubsup" id="MathJax-Span-47"><span style="display: inline-block; position: relative; width: 1.634em; height: 0px;"><span style="position: absolute; clip: rect(3.117em, 1000.65em, 4.2em, -1000em); top: -4em; left: 0em;"><span class="mi" id="MathJax-Span-48" style="font-family: MathJax_Math; font-style: italic;">L</span><span style="display: inline-block; width: 0px; height: 4em;"></span></span><span style="position: absolute; top: -3.85em; left: 0.681em;"><span class="texatom" id="MathJax-Span-49"><span class="mrow" id="MathJax-Span-50"><span class="mi" id="MathJax-Span-51" style="font-size: 70.7%; font-family: MathJax_Math; font-style: italic;">p</span><span class="mo" id="MathJax-Span-52" style="font-size: 70.7%; font-family: MathJax_Main;">,</span><span class="mi" id="MathJax-Span-53" style="font-size: 70.7%; font-family: MathJax_Math; font-style: italic;">q<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.01em;"></span></span></span></span><span style="display: inline-block; width: 0px; height: 4em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 2.333em;"></span></span></span><span style="display: inline-block; overflow: hidden; vertical-align: -0.442em; border-left: 0px solid; width: 0px; height: 1.379em;"></span></span></nobr><span class="MJX_Assistive_MathML" role="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>L</mi><mrow class="MJX-TeXAtom-ORD"><mi>p</mi><mo>,</mo><mi>q</mi></mrow></msub></math></span></span><script type="math/tex" id="MathJax-Element-9">L_{p, q}</script>范数</a></li><li><a rel="nofollow" href="#_lab2_0_10">11. 矩阵的核范数及Schatten范数</a></li><li><a rel="nofollow" href="#_lab2_0_11">12. MATLAB程序:Laplace分布与Gauss分布的概率密度函数图</a></li><li><a rel="nofollow" href="#_lab2_0_12">13. 参考文献</a></li></ul></ul></div>
浅谈范数正则化
作者:凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/
这篇博客介绍不同范数作为正则化项时的作用。首先介绍了常见的向量范数与矩阵范数,然后说明添加正则化项的原因,之后介绍向量的
1. 向量范数与矩阵范数

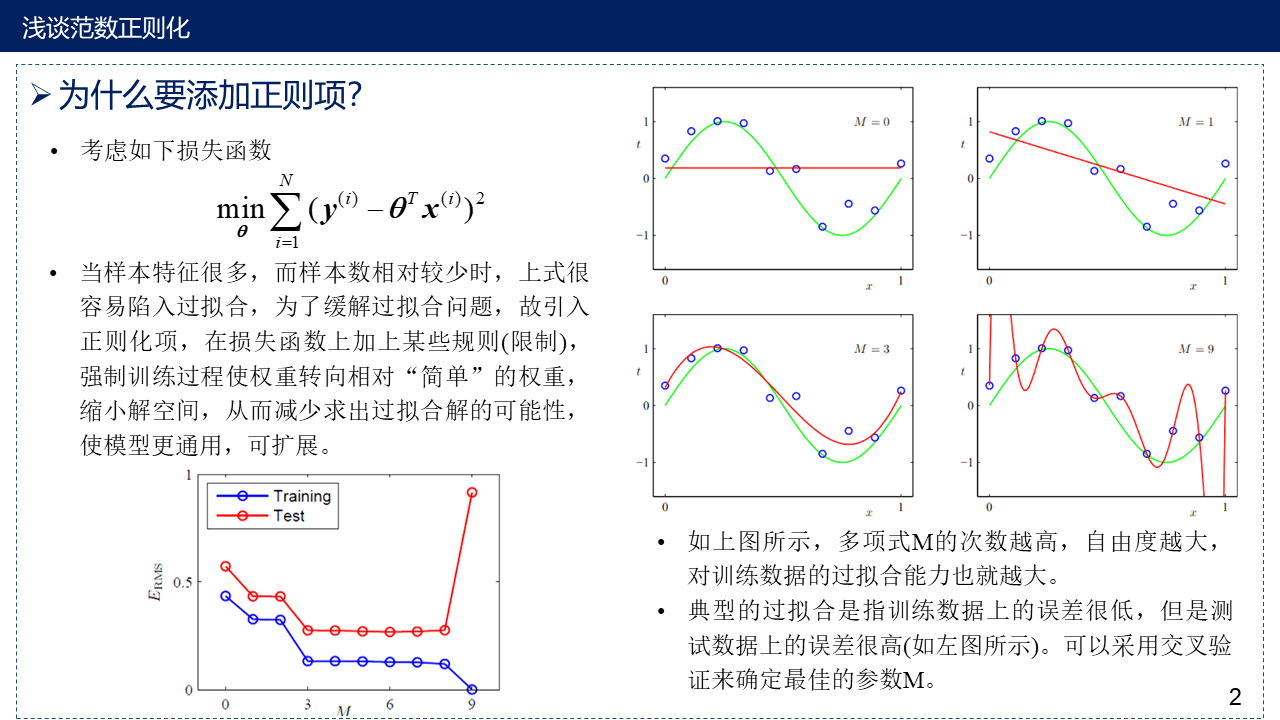
2. 为什么要添加正则项?
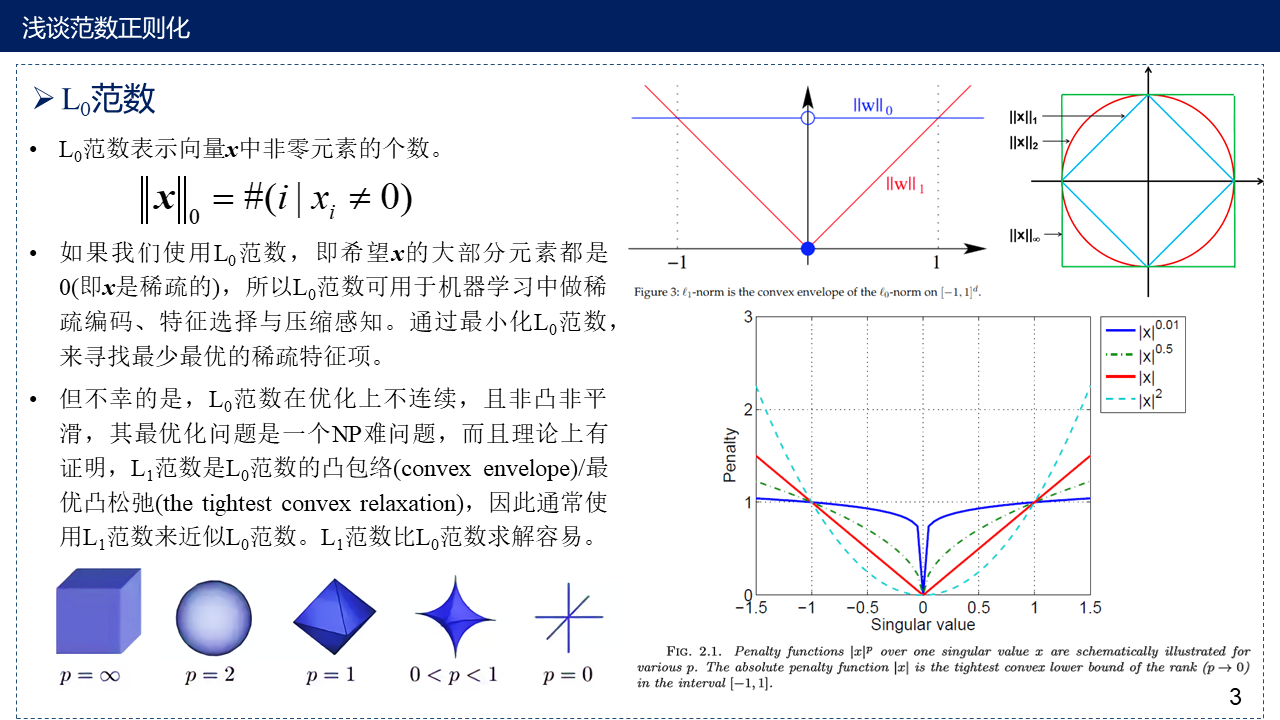
3. L0 范数
4. L1 范数

5. L2 范数

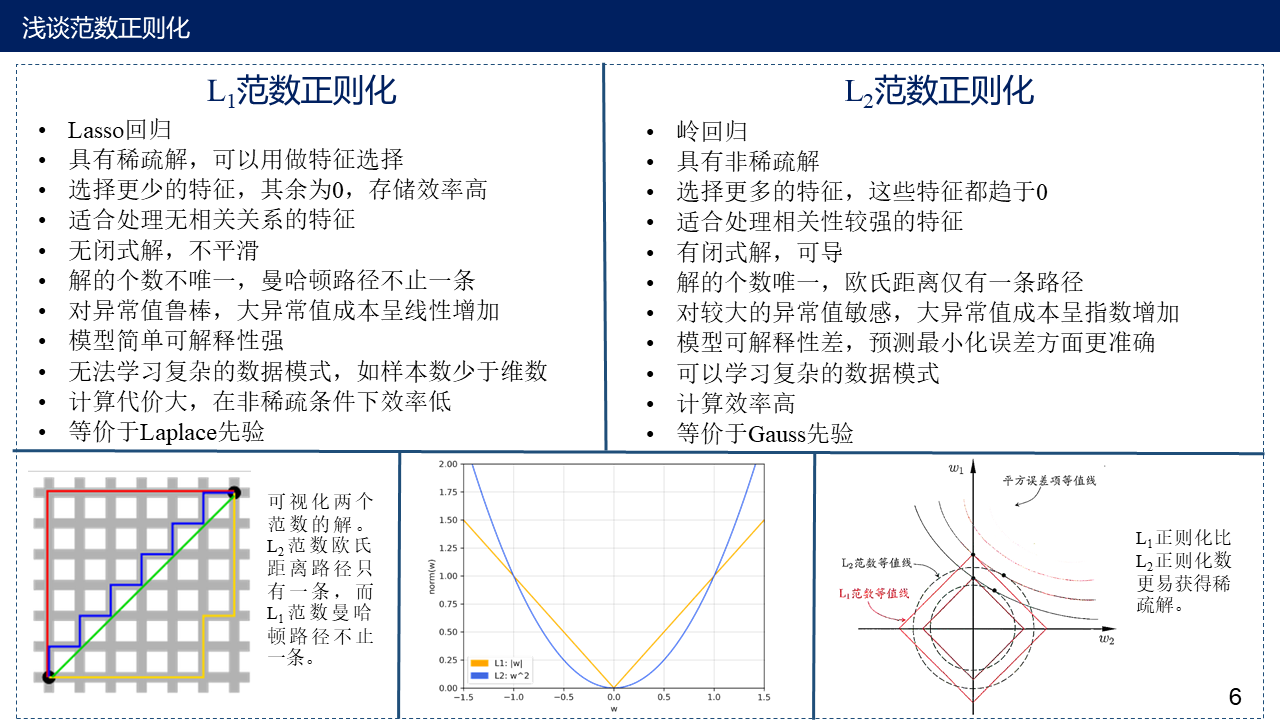
6. L1 范数与L2 范数作为正则项的区别
7. 用概率解释传统线性回归模型

8. L2 范等价于Gauss先验

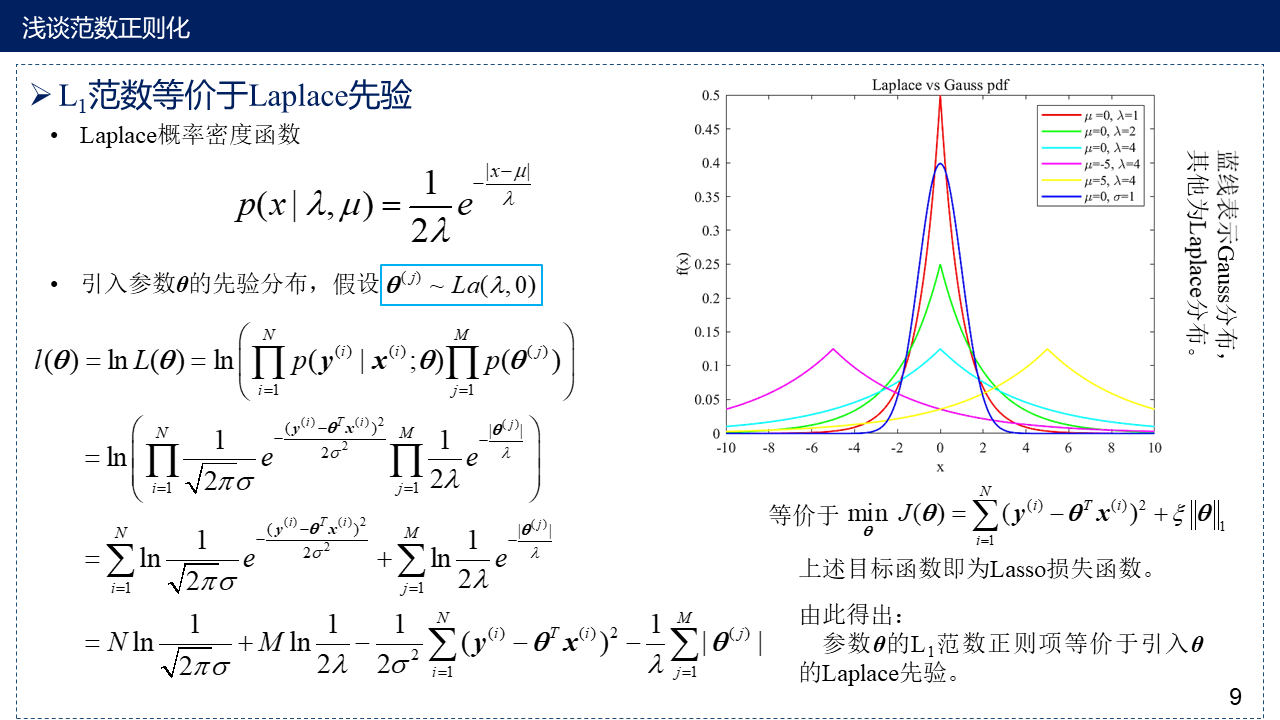
9. L1 范数等价于Laplace先验
10. 矩阵的L2,1 范数及Lp,q 范数

11. 矩阵的核范数及Schatten范数

12. MATLAB程序:Laplace分布与Gauss分布的概率密度函数图
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | %% Demo of Laplace Density Function% x : variable% lambda : size para%miu: location paraclearclcx = -10:0.1:10;y_1=Laplace_distribution(x, 0, 1);y_2=Laplace_distribution(x, 0, 2);y_3=Laplace_distribution(x, 0, 4);y_4=Laplace_distribution(x, -5, 4);y_5=Laplace_distribution(x, 5, 4);y_6=normpdf(x,0,1);plot(x, y_1, 'r-', x, y_2, 'g-', x, y_3, 'c-', x, y_4, 'm-', x, y_5, 'y-', x, y_6, 'b-', 'LineWidth',1.2);legend('\mu =0, \lambda=1','\mu=0, \lambda=2','\mu=0, \lambda=4','\mu=-5, \lambda=4','\mu=5, \lambda=4', '\mu=0, \sigma=1'); %图例的设置xlabel('x');ylabel('f(x)');title('Laplace vs Gauss pdf');set(gca, 'FontName', 'Times New Roman', 'FontSize',11);saveas(gcf,sprintf('demo_Laplace_Gauss.jpg'),'bmp'); %保存图片%% Laplace Density Functionfunction y=Laplace_distribution(x, miu, lambda) y = 1 / (2*lambda) * exp( -abs(x-miu)/lambda);end |
13. 参考文献
[1] 证明核范数是矩阵秩的凸包络
EJ Candès, Recht B . Exact Matrix Completion via Convex Optimization[J]. Foundations of Computational Mathematics, 2009, 9(6):717.
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.312.1183&rep=rep1&type=pdf
[2] 关于说明
Donoho D L , Huo X . Uncertainty Principles and Ideal Atomic Decomposition[J]. IEEE Transactions on Information Theory, 2001, 47(7):2845-2862.
Learning with Combinatorial Structure Note for Lecture 12
http://people.csail.mit.edu/stefje/fall15/notes_lecture12.pdf
L1-norm Methods for Convex-Cardinality Problems
https://web.stanford.edu/class/ee364b/lectures/l1_slides.pdf
[3] 有关过拟合的教案及图片来源
2017 Lecture 2: Overfitting. Regularization
https://www.cs.mcgill.ca/~dprecup/courses/ML/Lectures/ml-lecture02.pdf
[4] 一些可供参考的资料
The difference between L1 and L2 regularization
https://explained.ai/regularization/L1vsL2.html
Why L1 norm for sparse models
https://stats.stackexchange.com/questions/45643/why-l1-norm-for-sparse-models
Why L1 regularization can “zero out the weights” and therefore leads to sparse models? [duplicate]
What are L1, L2 and Elastic Net Regularization in neural networks?
Introduction. Sharpness Enhancement and Denoising of Image Using L1-Norm Minimization Technique in Adaptive Bilateral Filter.
<div class="clear"></div>
<div id="post_next_prev">
<a href="https://www.cnblogs.com/kailugaji/p/14613210.html" class="p_n_p_prefix">« </a> 上一篇: <a href="https://www.cnblogs.com/kailugaji/p/14613210.html" title="发布于 2021-04-03 10:14">一类涉及矩阵范数的优化问题</a>
<br>
<a href="https://www.cnblogs.com/kailugaji/p/14682575.html" class="p_n_p_prefix">» </a> 下一篇: <a href="https://www.cnblogs.com/kailugaji/p/14682575.html" title="发布于 2021-04-20 19:54">MATLAB数值实验:函数逼近法求方程的数值解</a>
搜索
</div>
</div>
我的标签
积分与排名
- 积分 - 372666
- 排名 - 1568
<h1 class="catListTitle">
随笔分类
(111)
</h1>
<ul class="catList">
<li class="catListItem" data-category-list-item-visible="true" style="display: block">
</li> <li class="catListItem" data-category-list-item-visible="true" style="display: block">
</li> <li class="catListItem" data-category-list-item-visible="true" style="display: block">
</li> <li class="catListItem" data-category-list-item-visible="true" style="display: block">
</li> <li class="catListItem" data-category-list-item-visible="true" style="display: block">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem"><a href="javascript:void(0)" onclick="sideColumnManager.loadMore(this)">更多</a></li>
</ul>
<h1 class="catListTitle">
随笔档案
(245)
</h1>
<ul class="catList">
<li class="catListItem" data-category-list-item-visible="true" style="display: block">
</li> <li class="catListItem" data-category-list-item-visible="true" style="display: block">
</li> <li class="catListItem" data-category-list-item-visible="true" style="display: block">
</li> <li class="catListItem" data-category-list-item-visible="true" style="display: block">
</li> <li class="catListItem" data-category-list-item-visible="true" style="display: block">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem" data-category-list-item-visible="false" style="display: none">
</li> <li class="catListItem"><a href="javascript:void(0)" onclick="sideColumnManager.loadMore(this)">更多</a></li>
</ul>
<h1 class="catListTitle">
文章档案
(2)
</h1>
<ul class="catList">
<li class="catListItem" data-category-list-item-visible="true" style="display: block">
</li> <li class="catListItem" data-category-list-item-visible="true" style="display: block">
</li>
</ul>
<h1 class="catListTitle">
我的其他博客
</h1>
<ul class="catList">
<li class="catListItem" data-category-list-item-visible="true" style="display: block">
</li> <li class="catListItem" data-category-list-item-visible="true" style="display: block">
</li>
</ul>
最新评论
- 1. Re:MATLAB实例:构造网络连接图(Network Connection)及计算图的代数连通度(Algebraic Connectivity)
- @我住隔壁不姓王 那只能控制节点位置的随机性了,尽量放置节点时让其方差小一点,紧凑一点。或者尽可能均匀分布在区域内。...
- --凯鲁嘎吉
- 2. Re:MATLAB实例:构造网络连接图(Network Connection)及计算图的代数连通度(Algebraic Connectivity)
- @凯鲁嘎吉 谢谢回复,但是这个不稳定啊,还是会存在所有节点不连接的情况 我想实现在规定区域内和规定的通信距离,将放置的所有节点连接起来(保证一个节点能连接两个节点),不会存在孤点的情况 ,只需要构造网...
- --我住隔壁不姓王
- 3. Re:MATLAB实例:构造网络连接图(Network Connection)及计算图的代数连通度(Algebraic Connectivity)
- @我住隔壁不姓王 增大通信距离或缩小区域面积 Conf.Square = 3.5; %方形区域的边长 Conf.CommDist = 0.8; %最大通信距离 调这两个参数...
- --凯鲁嘎吉
- 4. Re:MATLAB实例:构造网络连接图(Network Connection)及计算图的代数连通度(Algebraic Connectivity)
请问如何将孤点也连接起来呢(或者只需要保证每个节点能连接起来也可以)
- --我住隔壁不姓王
- 5. Re:MATLAB用“fitgmdist”函数拟合高斯混合模型(一维数据)
- @我是皇小楠 把概率密度这一列当做数据data...
- --凯鲁嘎吉
<div id="page_end_html">
<script>(function(T,h,i,n,k,P,a,g,e){g=function(){P=h.createElement(i);a=h.getElementsByTagName(i)[0];P.src=k;P.charset="utf-8";P.async=1;a.parentNode.insertBefore(P,a)};T["ThinkPageWeatherWidgetObject"]=n;T[n]||(T[n]=function(){(T[n].q=T[n].q||[]).push(arguments)});T[n].l=+new Date();if(T.attachEvent){T.attachEvent("onload",g)}else{T.addEventListener("load",g,false)}}(window,document,"script","tpwidget","//widget.seniverse.com/widget/chameleon.js"))</script>
<input type="hidden" id="antiforgery_token" value="CfDJ8FO3GXnjClZGrNGr2Ic8Z1qpRZD0rt1_jnxLR58Zdr9yaz3DSUkQIc6gWcE7xdcR78VyDMTSVu4vjQ8kdD7maER52PVR5ccStTOyrpVxxA0ZrKNyyThJsUFTszjvHWo4B2qiF6avlKdxdlLKEuCGHzdCIHDLahVNbc3YbHK-NzTtr8qq_pESi1e-LZ7WIpW3wg">







不改了 退出 订阅评论 我的博客
[Ctrl+Enter快捷键提交]
【推荐】百度智能云超值优惠:新用户首购云服务器1核1G低至69元/年
【推荐】跨平台组态\工控\仿真\CAD 50万行C++源码全开放免费下载!
【推荐】和开发者在一起:华为开发者社区,入驻博客园科技品牌专区
· 理解ASP.NET Core - 选项(Options)
· 跳槽一年后的回顾
· 在 Unity 中渲染一个黑洞
· 理解 ASP.NET Core - 配置(Configuration)
· CSS 奇技淫巧 | 妙用 drop-shadow 实现线条光影效果
· Google Cloud现在将显示其用户在云中的碳足迹(2021-10-13 08:33)
· 微软称其抵挡了有史以来最大的DDoS攻击 带宽负载高达2.4Tbps(2021-10-13 08:25)
· OpenSilver将接替退休的微软Silverlight的工作(2021-10-13 08:16)
· 现代宇宙学模拟超大质量黑洞(SMBH)在宇宙中游荡(2021-10-13 08:08)
· Reddit聘请前Google云计算主管为其首位首席产品官(2021-10-13 08:01)
» 更多新闻...