深度优先搜索DFS和广度优先搜索BFS

------------恢复内容开始------------

深度优先搜索DFS

一、简介

二、算法思想

　　优先访问最后一个被访问的顶点的未被访问的相邻结点（递归）

　　DFS在访问图中某一 起始顶点v后，由v出发，访问它的任一邻接顶点w1;

　　再从w1出发，访问与w1邻接但还没有访问过的顶点w2;然后再从w2出发，进行类似的访问，...

　　如此进行下去，直至到达所有的邻接顶点都被访问过的顶点u为止。
　　接着,退回一步，退到前一次刚访问过的顶点，看是否还有其它没有被访问的邻接顶点。
　　　　■如果有,则访问此顶点，之后再从此顶点出发，进行与前述类似的访问;
　　　　■如果没有，就再退回-步进行搜索。
　　　　■重复上述过程，直到连通图中所有顶点都被访问过为止。

　　图示过程：（遍历过程不唯一）

　　

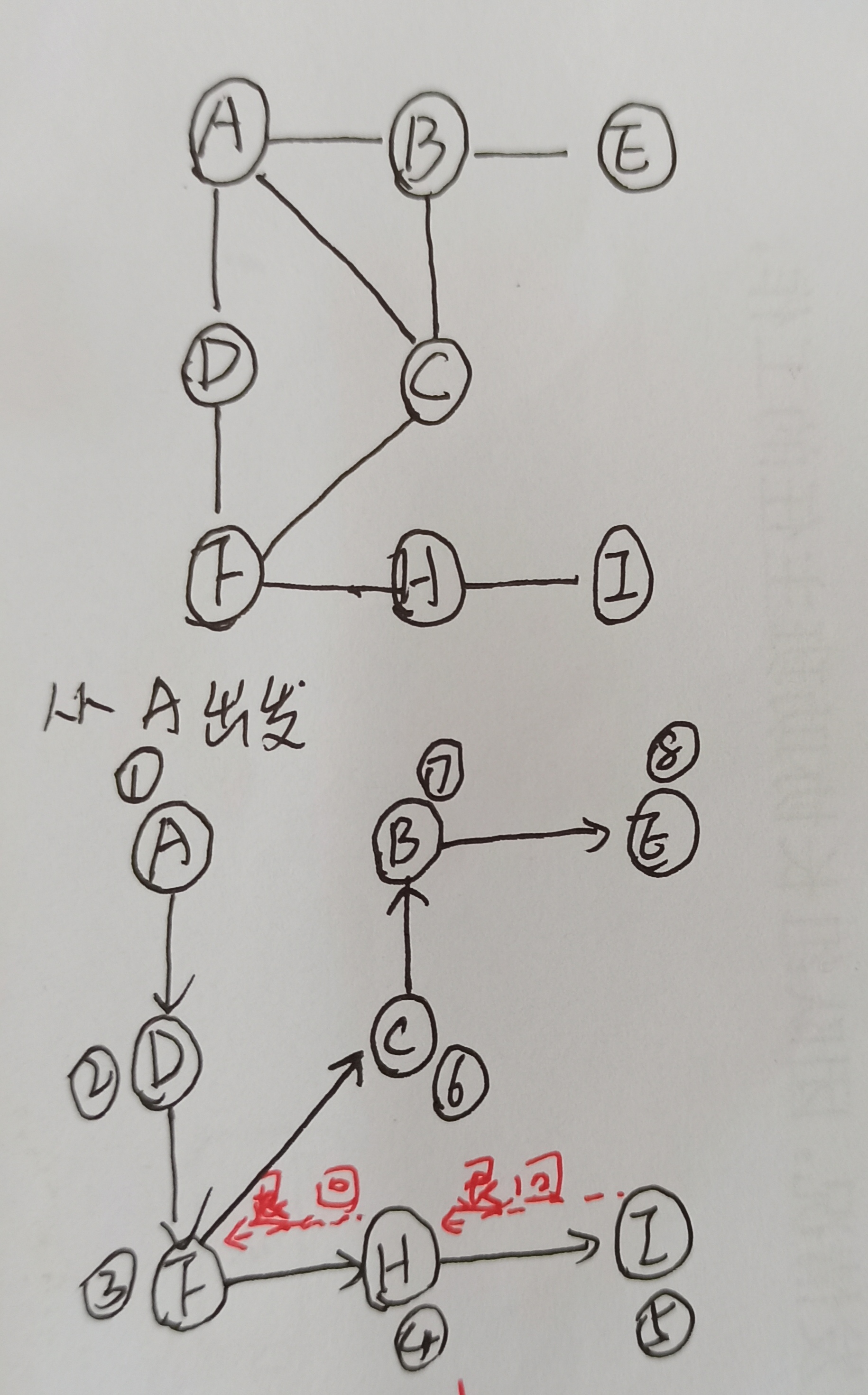
　　遍历序列：A->D->F->H->I->C->B->E

三、伪代码

void DFS(Graph* G,int v)//从图的某个顶点开始遍历
{
    Previsit(G,v);
    G->SetMark(v,VISIT);//设置访问标记 
    for(int w=G->first(v);w<G->n();w=G->next(v,w))
    {
        if(G->GetMark(w)==UNVISIT)
        {//如果没有被访问过，则访问v的临界顶点 
            DFS(G,w);
        }
    } 
    Postvisit(G,v);
} 

四、应用实例

广度优先搜索BFS

一、简介

二、算法思想

　　优先访问一个顶点的全部相邻结点（层次遍历）
　　在访问了起始顶点v之后，依次访问v的各个未曾被访问过的邻接顶点w1, w2, ... w,,然后再顺序访问w1, w2, ...w,的所有还未被访问过的邻接顶点。如此做下去，直到

　　图中所有顶点都被访问到为止。

　　图示过程：

　　

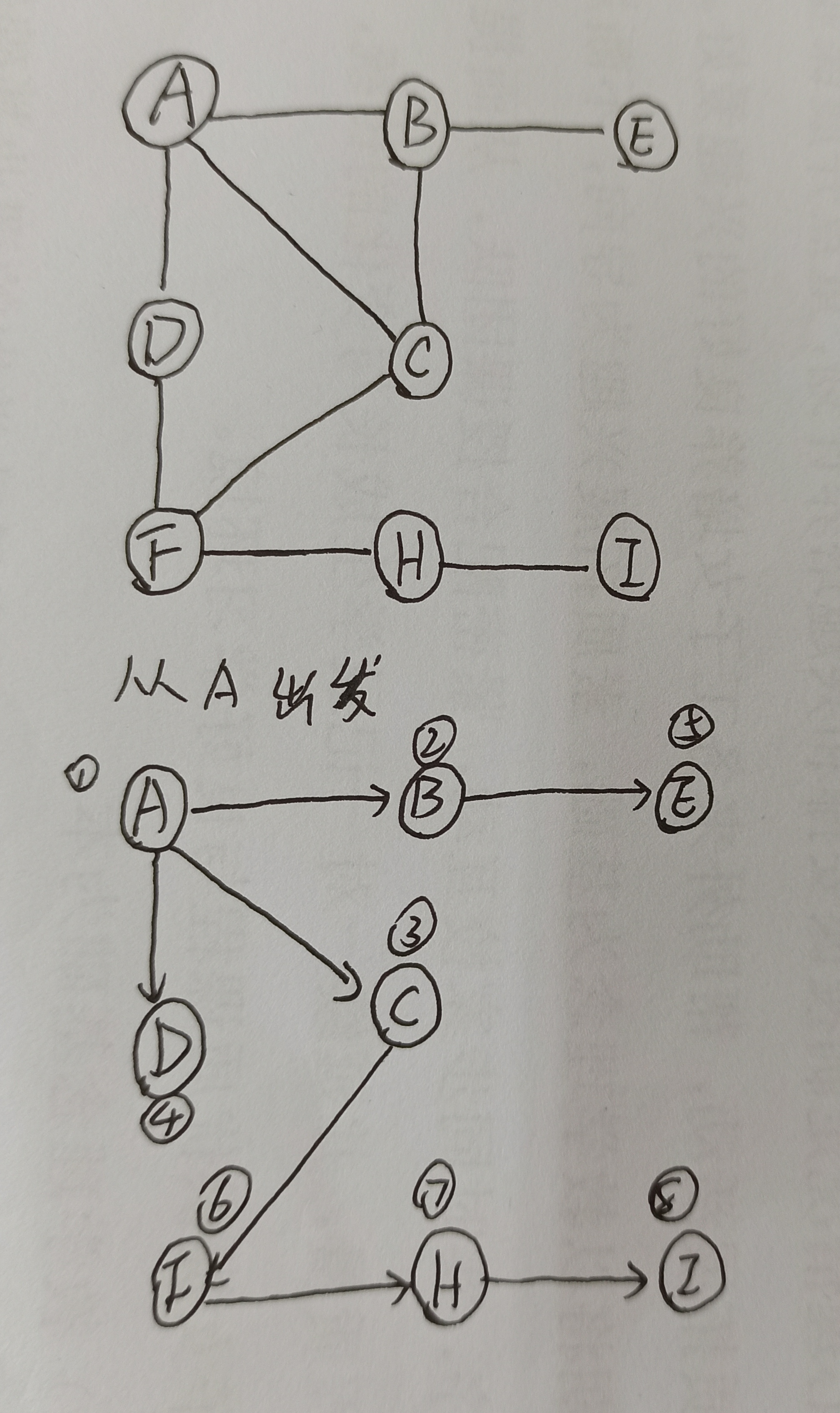
　　遍历序列：A->B->C->D->E->F->H->I

三、伪代码

void BFS(Graph* G,int v,queue<int>* Q)//从图的某个顶点开始遍历
{
    int v,w;
    Q->enqueue(v);//入队列 
    G->SetMark(v,VISIT);//设置访问标记 
    while(Q->length()!=0)
    {
        v=Q->dequeue();//出队列，开始遍历 
        Previsit(G,v);
        for(int w=G->first(v);w<G->n();w=G->next(v,w))
        {
            if(G->GetMark(w)==UNVISIT)
            {
                G->SetMark(w,VISIT);
                Q->enqueue(w);
            }
        } 
        Postvisit(G,v);
    }
}

四、应用实例

DFS VS BFS

未完

------------恢复内容结束------------