[leetcode]84. Largest Rectangle in Histogram直方图中的最大矩形

Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

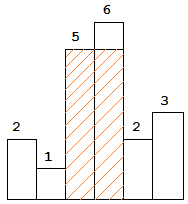
The largest rectangle is shown in the shaded area, which has area = 10 unit.

Example:

Input: [2,1,5,6,2,3]
Output: 10

 

题意：

给定一个直方图，求其能覆盖的最大矩形。

 

思路：

以下是O(n²) 的时间复杂度解法

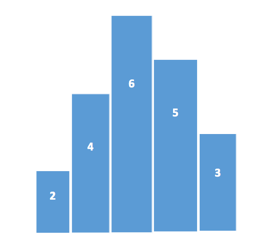
 当 i=  0       1 　　2　　 3　　 4

area= 2*1    4*1    6*1    5*1    3*1

                 2*2    4*2   5*2    3*2

                          2*3   4*3    3*3

                                  2*4    3*4

                                           2*5

以height[i]为临界，每次比较其左侧的所有height谁更小，更新minHeight, 更新当前maxArea

class Solution {
    public int largestRectangleArea(int[] heights) {
        int maxArea = 0;
        for(int i = 0; i < heights.length; i++){
            int minHeight = heights[i]; //以height[i]为临界
            for(int j = i; j >= 0; j--){ // 每次比较其左侧的所有height谁更小
                minHeight = Math.min(minHeight, heights[j]);
                maxArea = Math.max(maxArea, minHeight * (i - j + 1));
            }
        }
       return maxArea; 
    }
}

 

                       

以下是O(n) 的时间复杂度解法

维护一个单调栈monoStack，数组中每个元素的index都入栈、出栈

代码：

class Solution {
    public int largestRectangleArea(int[] heights) {
        Stack<Integer> s = new Stack<>();
        int area = 0;
        for(int i=0; i<= heights.length;){
            int value = i< heights.length ? heights[i]: 0;
                if(s.isEmpty() || value> heights[s.peek()]){
                    s.push(i);
                    i++;       
        }else{
            int temp = s.pop();
            area = Math.max(area, heights[temp] * (s.isEmpty() ? i: (i-s.peek()-1)));
        }
        
       
    }
         return area;
   }
}