[leetcode]15. 3Sum三数之和

Given an array nums of n integers, are there elements a, b, c in nums such that a + b + c = 0? Find all unique triplets in the array which gives the sum of zero.

Note:

The solution set must not contain duplicate triplets.

Example:

Given array nums = [-1, 0, 1, 2, -1, -4],

A solution set is:
[
  [-1, 0, 1],
  [-1, -1, 2]
]

 

题意：

给定一个数组和一个值target，找到所有三数加起来等于target的组合

 

Solution1：Two Pointers(left and right to meet each other)

1. Sort the array (coz we must check the duplicates) 

2. Lock one pointer and do two sum with the other two

 

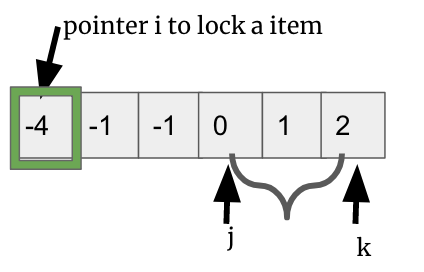
Step1: Sort the given array in ascending order

Step2: Lock pointer i, then do two sum with two pointers j, k

 

Step3:  checking nums[i] + nums[j] + nums[k] == target ? 

           if   nums[i] + nums[j] + nums[k] < target,  pointer j ++

           if   nums[i] + nums[j] + nums[k] > target,  pointer k --

                       

注意几点：

1、题目要求“The solution set must not contain duplicate triplets.” 每次移动 i , j , k 都注意查重

2、Arrays工具类中常用方法需要牢记：

Arrays.sort() 排序数组

Arrays.fill() 填充数组

Arrays.toString() 将int数组转成string数组

Arrays.asList() 将数组转成list集合

 

code:

/*
    Time Complexity: O(n^2). For each locked item, we need traverse the rest of array behind such item.  
    Space Complexity: O(1).  We only used constant extra space.
*/
class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        int target = 0;
        Arrays.sort(nums);
        // corner case
        if (nums.length < 3) return result;

        for (int i = 0; i < nums.length; i++) {
            if (i > 0 && nums[i] == nums[i - 1]) continue;   // skip duplicates
            int j = i + 1;
            int k = nums.length - 1;
            while (j < k) {
                if (nums[i] + nums[j] + nums[k] < target) {
                    j++;
                    while (j < k && nums[j] == nums[j - 1]) j++; // skip duplicates
                } else if (nums[i] + nums[j] + nums[k] > target) {
                    k--;
                    while (j < k && nums[k] == nums[k + 1]) k--; // skip duplicates
                } else {
                    result.add(Arrays.asList(nums[i], nums[j], nums[k]));
                    j++;
                    k--;
                    while (j < k && nums[j] == nums[j - 1]) j++; // skip duplicates
                    while (j < k && nums[k] == nums[k + 1]) k--; // skip duplicates
                }
            }
        }
        return result;
    }
}