[leetcode]87. Scramble String字符串树形颠倒匹配

Given a string s1, we may represent it as a binary tree by partitioning it to two non-empty substrings recursively.

Below is one possible representation of s1 = "great":

 great
   /    \
  gr    eat
 / \    /  \
g   r  e   at
           / \
          a   t

To scramble the string, we may choose any non-leaf node and swap its two children.

For example, if we choose the node "gr" and swap its two children, it produces a scrambled string "rgeat".

   rgeat
   /    \
  rg    eat
 / \    /  \
r   g  e   at
           / \
          a   t

 

题意：

对于一个字符串，若通过一些列树形颠倒（确定一点后，前后子串交换）得到一个新的字符串，则互为Scramble String

 

思路：

这道题面试很低频，因为若要dp解，则需三维dp，难度很高不适合面试

直接用递归，观察规律：

若s1 和 s2 长度都为1 ： 两字符串必须完全相当

若s1 和 s2 长度都为2： 则当s1 = "ab"时， s2 = "ab" || "ba"

若s1 和 s2 长度都为3： 将 s1 分成 s1Left 和 s1Right两部分

                                    s2 分成 s2Left 和 s2Right 两部分

                                  则 ( s1Left  isScrambled s2Left  && s1Right isScrambled s2Right ) 或者  (s1Left  isScrambled s2Right && s1Right isScrambled s2Left  ) 

如图，

 

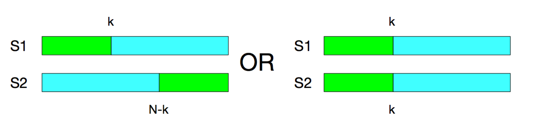
所以，

先判断s1和s2是否是valid anagram (变位词)： 意味着两个字符串长度一致，互相只是各个字符串变换了位置

再递归生成s1的左边、右边，s2 的左边、右边

递归出口： s1等于s2 return true

 

代码：

class Solution {
    public boolean isScramble(String s1, String s2) {
         // corner
        if(s1.length() != s2.length() || s1 == null || s2 == null) return false;
        // recursion 出口
        if(s1.equals(s2)) return true; // 一定要加，否则recursion 没有出口
        // valid anagram or not 
        int[]map = new int[256];
        for(int i = 0; i < s1.length(); i++){
            map[s1.charAt(i)] ++;
            map[s2.charAt(i)] --;
        } 
        for(int i : map){
            if( i != 0){
                return false;
            }
        }
        // recursion 
        for(int i = 1; i < s1.length(); i++){ 
        if(isScramble(s1.substring(0,i), s2.substring(0,i)) && isScramble(s1.substring(i), s2.substring(i))) return true;
        if(isScramble(s1.substring(0,i), s2.substring(s2.length()-i)) && isScramble(s1.substring(i), s2.substring(0, s2.length()-i))) return true;
              
        } 
       return false;
    }
    
}