[leetcode]272. Closest Binary Search Tree Value II二叉搜索树中最近的值II

Given a non-empty binary search tree and a target value, find k values in the BST that are closest to the target.

Note:

• Given target value is a floating point.
• You may assume k is always valid, that is: k ≤ total nodes.
• You are guaranteed to have only one unique set of k values in the BST that are closest to the target.

Example:

Input: root = [4,2,5,1,3], target = 3.714286, and k = 2

    4
   / \
  2   5
 / \
1   3

Output: [4,3]

Follow up:
Assume that the BST is balanced, could you solve it in less than O(n) runtime (where n = total nodes)?

 

题意

和之前一样，不过这次要找的是最接近的k个值。

 

Solution1：

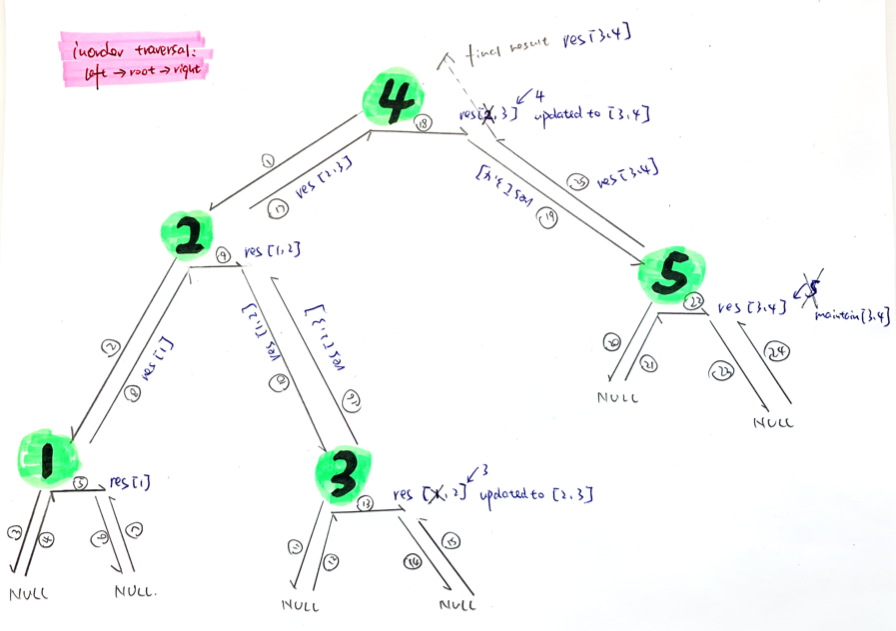
1.  Based on BST's attributes, if we traversal BST inorder,  each node will be in acsending order

2. we choose a data structure which can help operate on both sides(LinkedList or Deque), maintaining a K size sliding window

   once there is a new item, 

   we check diff (1) next item vs target

                      (2) leftMost item vs target

 

 

code

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */

/*
Time Complexity: O(n)
Space Complexity:O(k)
*/
class Solution {
    // choose a data structure which can do operations on both sides
    LinkedList<Integer> result = new LinkedList<>();
    
    public List<Integer> closestKValues(TreeNode root, double target, int k) {
        // corner case
        if (root == null) {return null;}
        // inorder traversal
        closestKValues(root.left, target, k);
    
        if (result.size() < k) {
            result.add(root.val);
            // maintain a K size sliding window such that items are closest to the target
        } else if(result.size() == k) {
            if (Math.abs(result.getFirst() - target) > (Math.abs(root.val - target))) {
                result.removeFirst();
                result.addLast(root.val);
            } 
        }
        // inorder traversal
        closestKValues(root.right, target, k);
        return result;
    }    
}