[leetcode]11. Container With Most Water存水最多的容器

Given n non-negative integers a1, a2, ..., an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.

Note: You may not slant the container and n is at least 2.

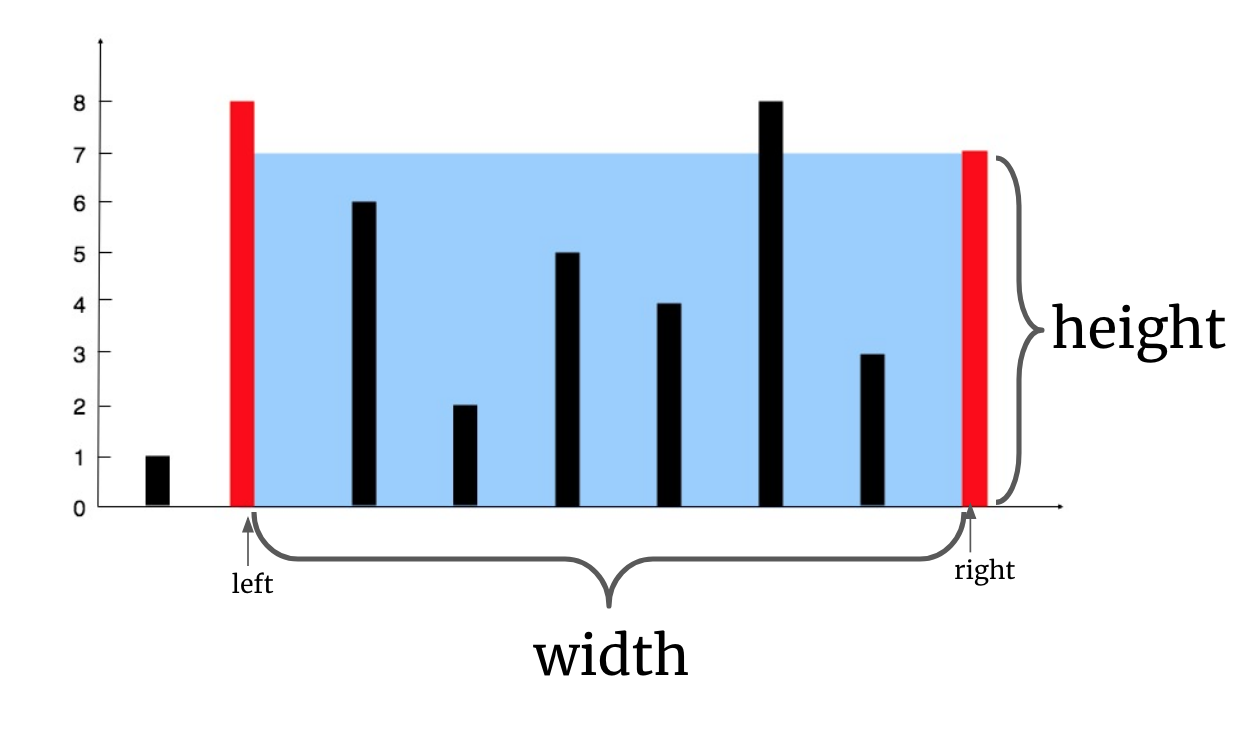
The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.

 

Example:

Input: [1,8,6,2,5,4,8,3,7]
Output: 49

题意：

给定一堆高矮不一的平行的墙，选择其中两堵作为两壁，问最多能存多少水。

 

Solution1：

Two Pointers:  set pointer left at index 0; set pointer right at index len - 1

We calculate area base on width (gap of left and right index ) and height(smaller height matters because of "Short-board effect" )

In order to find max area, we move the pointer whichever representing the smaller height

 

code:

/*
    Time complexity : O(n). We traverse the whole give array
    Space complexity : O(1). We only used constant extra space. 
*/

class Solution {
    public int maxArea(int[] height) {
        int left = 0;
        int right = height.length - 1;
        int area = Integer.MIN_VALUE;
        while(left < right){
            area = Math.max(area, Math.min(height[left], height[right]) * (right - left)); 
            if(height[left] < height[right]){
                left ++;
            }else{
                right --;
            }    
        }
      return area;  
    }
}