[leetcode]4. Median of Two Sorted Arrays俩有序数组的中位数

There are two sorted arrays nums1 and nums2 of size m and n respectively.

Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).

You may assume nums1 and nums2 cannot be both empty.

Example 1:

nums1 = [1, 3]
nums2 = [2]

The median is 2.0

Example 2:

nums1 = [1, 2]
nums2 = [3, 4]

The median is (2 + 3)/2 = 2.5

 

Solution1: time complexity is O(m+n). merge two sorted array, then find the median

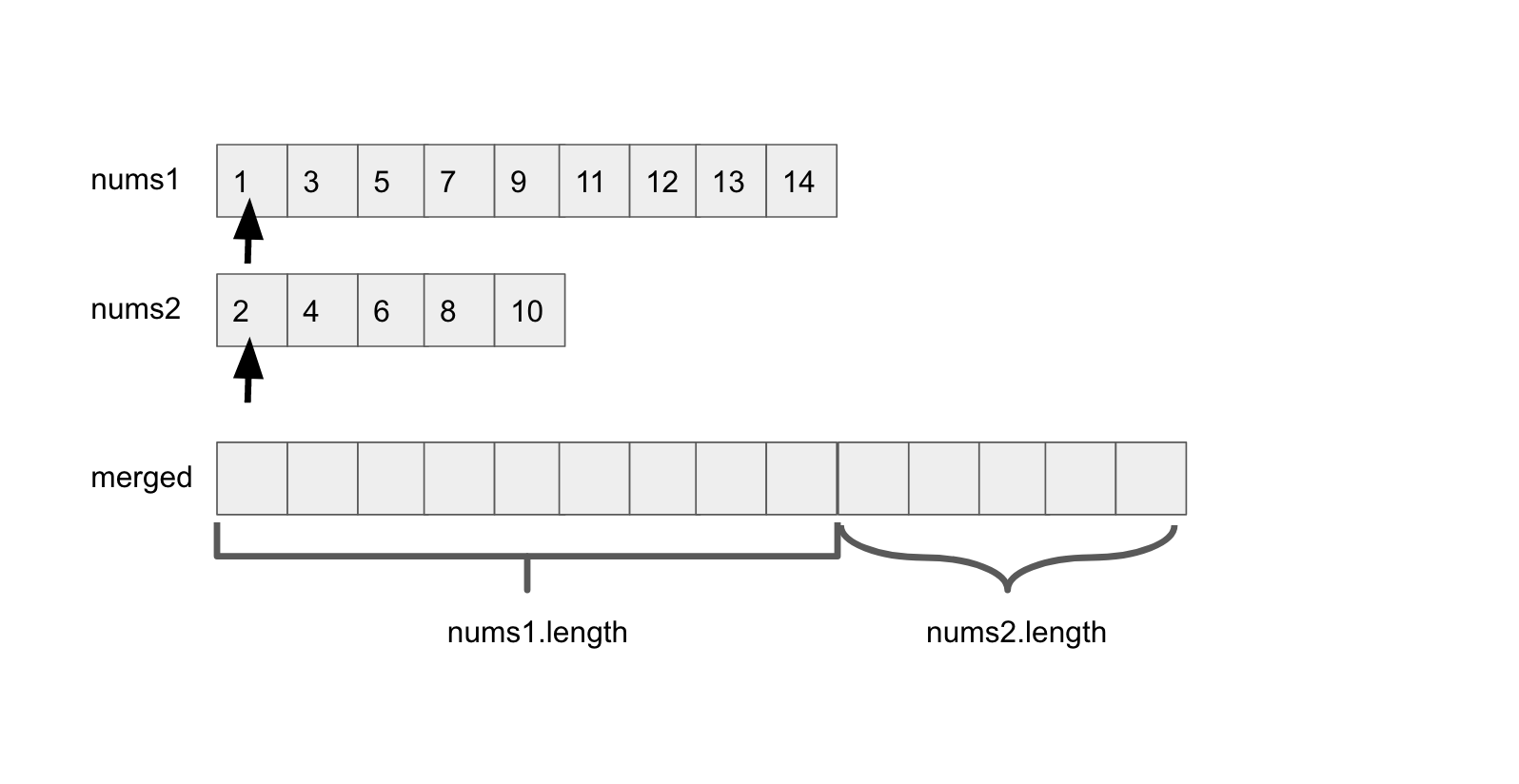
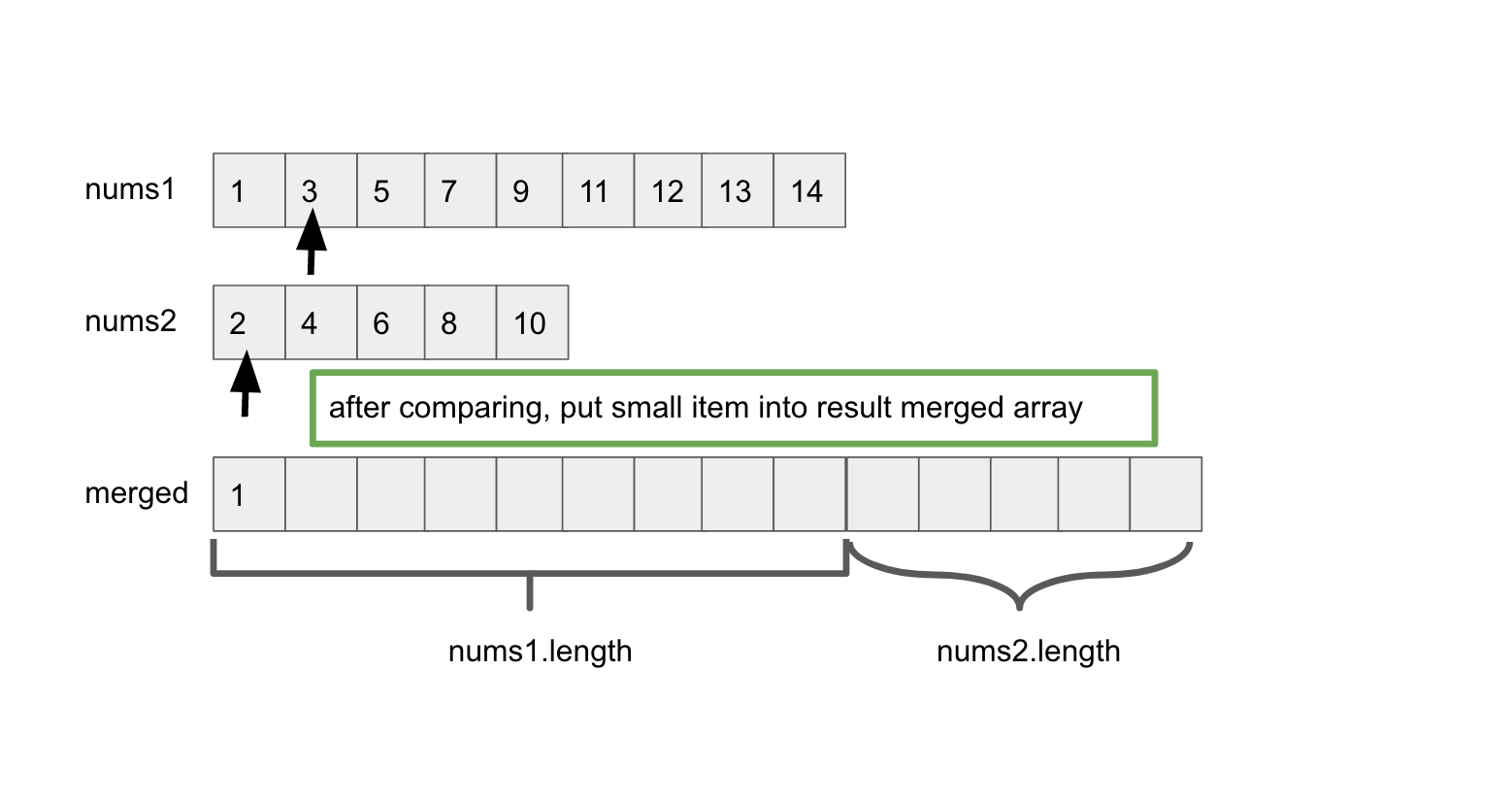
code:

/*
  Time Complexity:  O(m+n)
  Space Complexity: O(m+n) 
*/

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {   // find median
        int[] mergedArray = mergeTwoSortedArray(nums1, nums2);
        int n = mergedArray.length; 
        if( n % 2 == 0){
            return (mergedArray[(n-1)/2] + mergedArray[n/2])/2.0; 
        }else{
            return mergedArray[n/2]; 
        }
    } 
    
    public int[] mergeTwoSortedArray(int[] nums1, int[] nums2){ // merge sort
        int[] merged = new int[nums1.length + nums2.length];
        int i = 0, j = 0, k = 0;
        // 两个array同时扫
        while( i < nums1.length && j < nums2.length){
            merged[k++] = (nums1[i] < nums2[j]) ? nums1[i++] : nums2[j++]; 
        }
        //扫到只剩下较长的那个array， either nums1 or nums2
        while ( i < nums1.length ){
             merged[k++] = nums1[i++];
        }
        while(j < nums2.length){
            merged[k++] = nums2[j++];
        }
        return merged;
    }
}

 

Solution2: time complexity is O(log (m+n)). 

这个题的思路可以是找出2个sorted array 所有元素中，Kth 元素

因此我们可以把问题转化成，

“Given 2 sorted arrays, A, B of sizes m, n respectively, find the numbers which are NOT medians of the two sorted arrays”

如果我们能找到那些NOT medians的数字，删掉，并不断缩小范围，那最终剩下的一定就是actual median

 

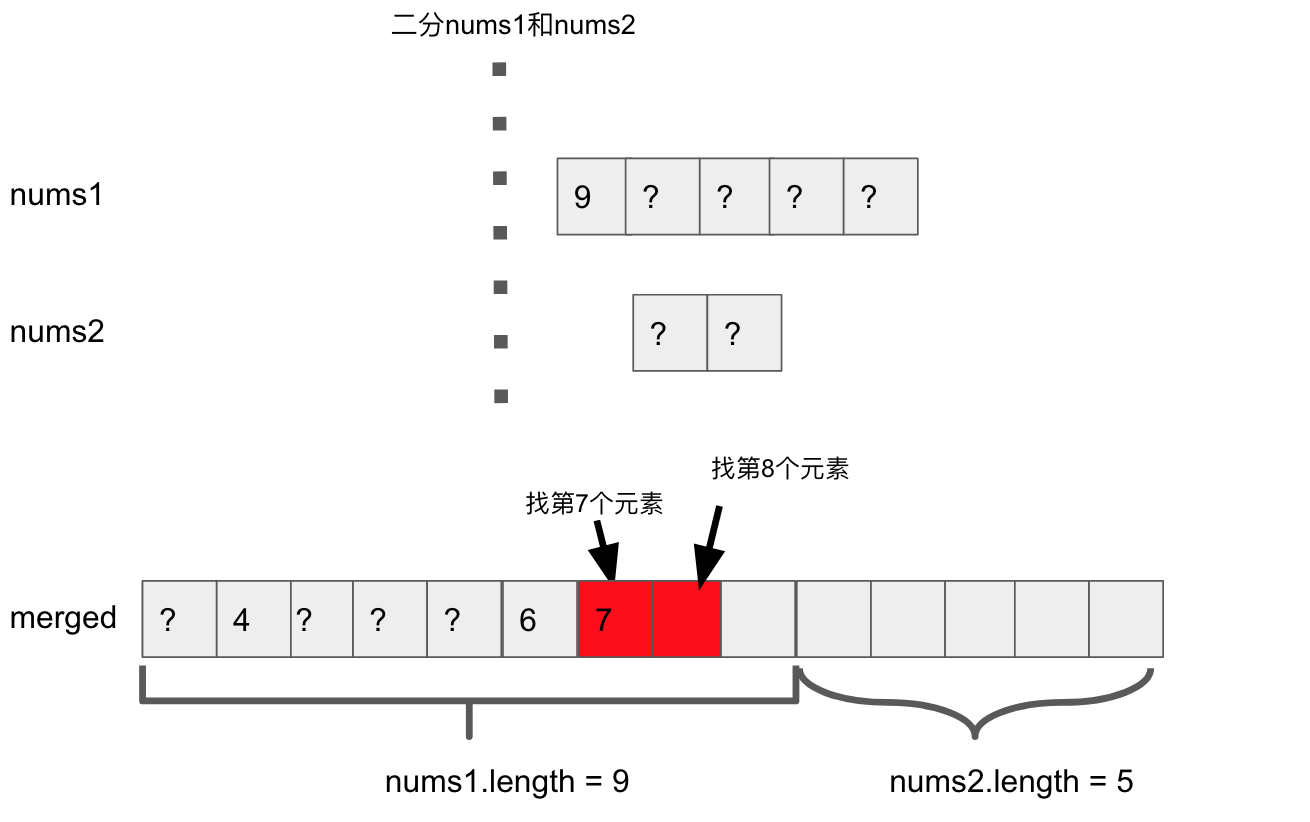
Step1, 确定要找的median是merged之后array中的第几个元素

 

 

Step2, 用binary search切开nums1, nums2。发现nums1左半边的长度为4， nums2左半边的长度为2。

 

Step3, nums1左半边长度+ nums2左半边长度为6

 

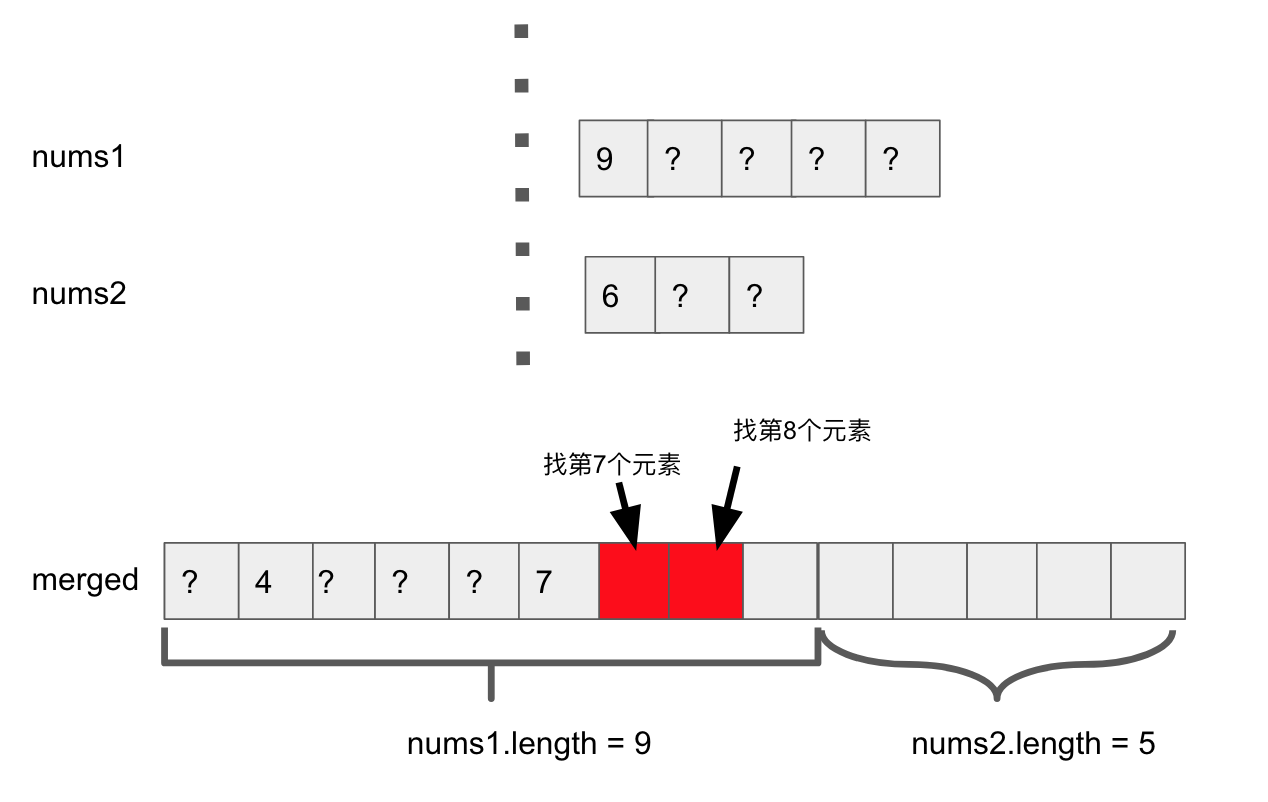
Step4， 所以第7个元素可能在nums1的右半边pivot上，或者在nums2的右半边pivot上

 

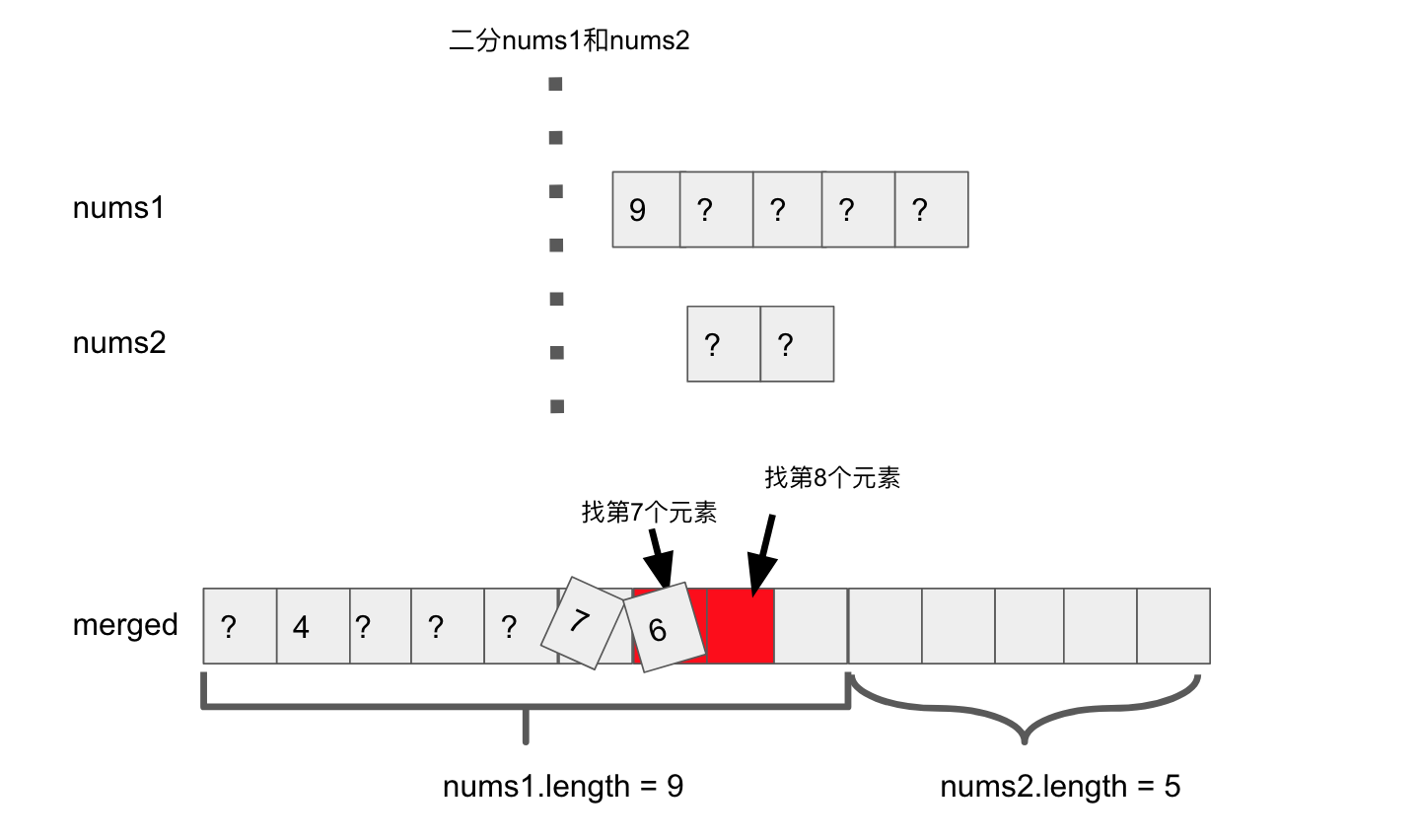
比较发现，第7个元素应该是7

 

 

code：

/*
 Time Complexity: O(log(m+n))
 Space Complexity: O(log(m+n))
*/

class Solution {
    public double findMedianSortedArrays(final int[] A, final int[] B) {
        int total = A.length + B.length;
        if (total %2 == 0){
            return (findKth(A, 0, B, 0, total / 2) + findKth(A, 0, B, 0, total / 2 + 1)) / 2.0;
        }else{
            return findKth(A, 0, B, 0, total / 2 + 1);
        }
    }

    private static int findKth(final int[] A, int ai, final int[] B, int bi, int k) {
        //always assume that A is shorter than B
        if (A.length - ai > B.length - bi) {
            return findKth(B, bi, A, ai, k);
        }
        if (A.length - ai == 0) return B[bi + k - 1];
        if (k == 1) return Math.min(A[ai], B[bi]);

        //divide k into two parts
        int k1 = Math.min(k / 2, A.length - ai), k2 = k - k1;
        if (A[ai + k1 - 1] < B[bi + k2 - 1])
            return findKth(A, ai + k1, B, bi, k - k1);
        else if (A[ai + k1 - 1] > B[bi + k2 - 1])
            return findKth(A, ai, B, bi + k2, k - k2);
        else
            return A[ai + k1 - 1];
    }
}