假设有这样一个神经网络，包含一个输入层I，一个隐藏层H，一个输出层O
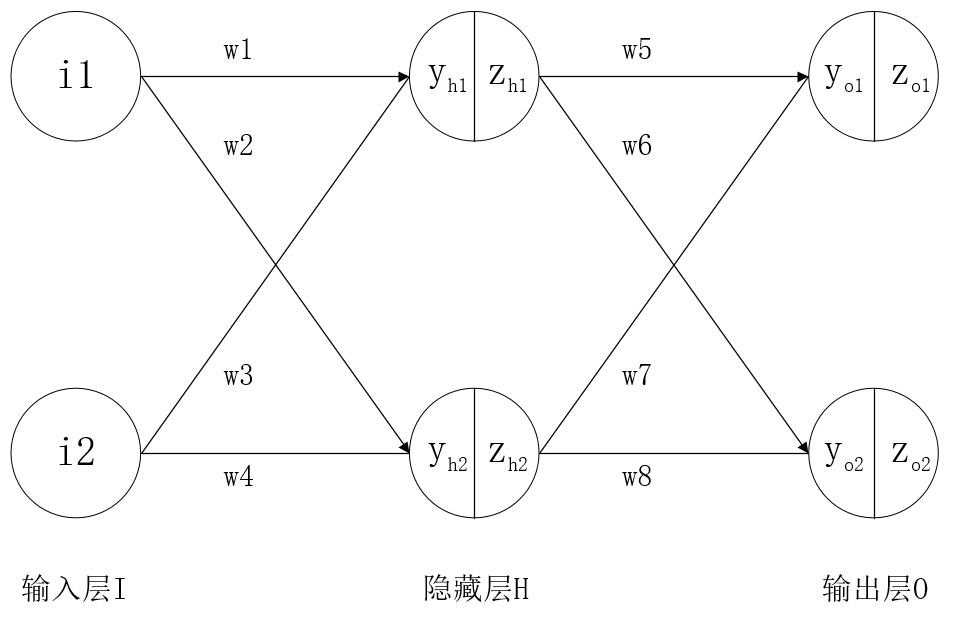
其中，输入层包含两个神经元，分别为i1和i2；隐藏层有两个神经元，分别为h1和h2；输出层有两个神经元，分别为o1和o2。
输入层到隐藏层的权重为w1、w2、w3和w4，偏置为b1；隐藏层到输出层的权重为w5、w6、w7和w8，偏置为b2。
每个神经元的输入y经过激活函数转变为输出z。
一、前向传播
1、计算隐藏层神经元h1和h2的带权输入：
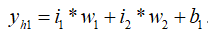
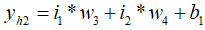
2、计算隐藏层神经元h1和h2的输出激活值：
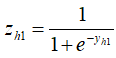
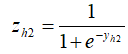
3、计算输出层神经元o1和o2的带权输入：
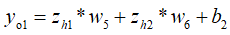
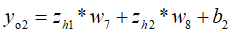
4、计算输出层神经元o1和o2的输出激活值：
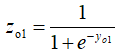
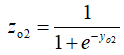
以上就是正向传播的整个过程。
二、反向传播
1、计算总误差：
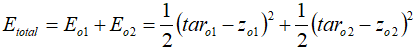
2、权值更新
以w5为例：
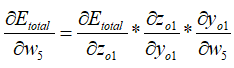
其中，
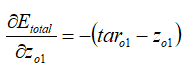
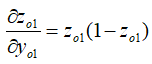
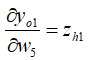
综合可得：
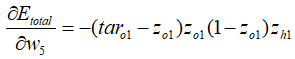
可以发现，最终得到的表达式非常简单，其中所需要的数据都是在正向传播过程中已经计算出来并存储好的，或者是在模型建立之初就已经设置好的。
最后更新w5：
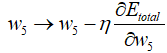
以w1为例：
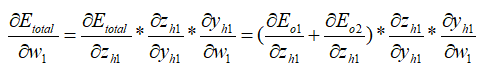
其中，
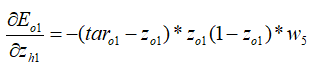
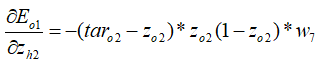
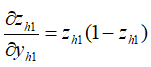
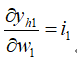
综上可得，
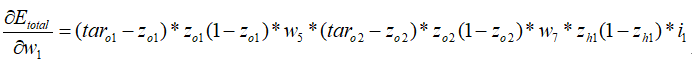
可以发现，最终得到的表达式非常简单，其中所需要的数据都是在正向传播过程中已经计算出来并存储好的，或者是在模型建立之初就已经设置好的。
最后更新w1：
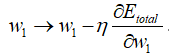
以上就是反向传播的过程。
三、梯度消失和梯度爆炸。
假设有一个神经网络，有1个输入层，4个隐藏层，1个输出层，每个层都只有1个神经元。
如果要更新w1这个权重，可以得到下面这个偏导数，
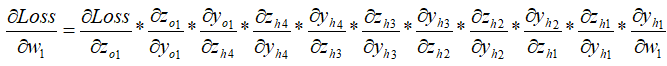
化简，
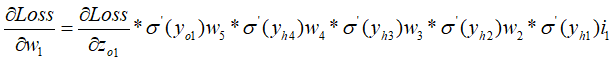
梯度消失与梯度爆炸都是由于网络层数过多而引发的在反向传播时的链式法则连乘效应。
在最初的时候，通常使用Sigmoid函数作为神经网络的激活函数，而sigmoid激活函数的导函数取值范围为(0,0.25)。在模型训练时，初始化权值w通常小于1，随着层数的增加，根据链式法则，小于1的数不断相乘，导致梯度消失。而当训练的权值过大时，即|S'(z)w|>1，大于1的值不断相乘，导致梯度爆炸。
在产生梯度消失或梯度爆炸的情况时，越接近输出层的层级，梯度相对更为正常，权值也接近正常，而接近输入层的层级，若产生了梯度消失，权值更新缓慢或停止更新，神经网络就等价于仅有靠近输出层的浅层网络。
总的来说：
如果|S'(z)w|<1，随着网络层数的不断加深，最终梯度将以指数形式减少（梯度消失）。
如果|S'(z)w|>1，随着网络层数的不断加深，最终梯度将以指数形式增加（梯度爆炸）。
