监督机器学习问题主要有两种,分别叫作分类(classification)与回归(regression)。
分类问题的目标是预测类别标签(class label),这些标签来自预定义的可选列表。在二分类问题中,我们通常将其中一个类别称为正类(positive class),另一个类别称为反 类(negative class)。这里的“正”并不代表好的方面或正数,而是代表研究对象。因此在 寻找垃圾邮件时,“正”可能指的是垃圾邮件这一类别。将两个类别中的哪一个作为“正 类”,往往是主观判断,与具体的领域有关。
回归任务的目标是预测一个连续值,编程术语叫作浮点数(floating-point number) ,数学术 语叫作实数(real number)。根据教育水平、年龄和居住地来预测一个人的年收入,这就是 回归的一个例子。在预测收入时,预测值是一个金额(amount),可以在给定范围内任意 取值。回归任务的另一个例子是,根据上一年的产量、天气和农场员工数等属性来预测玉 米农场的产量。同样,产量也可以取任意数值。
区分分类任务和回归任务有一个简单方法,就是问一个问题:输出是否具有某种连续性。 如果在可能的结果之间具有连续性,那么它就是一个回归问题。
泛化、过拟合与欠拟合
如果一个模型能够对没见过的数据做出准确 预测,我们就说它能够从训练集泛化(generalize)到测试集。我们想要构建一个泛化精度 尽可能高的模型。
如果你在拟合模型时过分关注训练集的细节,得到了一个在训练 集上表现很好、但不能泛化到新数据上的模型,那么就存在过拟合。与之相反,如果你 的模型过于简单——比如说,“有房子的人都买船”——那么你可能无法抓住数据的全部 内容以及数据中的变化,你的模型甚至在训练集上的表现就很差。选择过于简单的模型 被称为欠拟合(underfitting)。
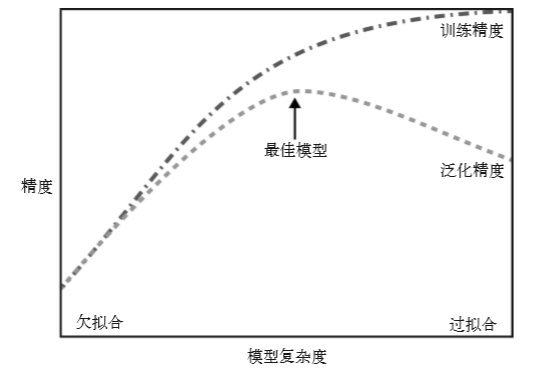
模型复杂度与数据集大小的关系
需要注意,模型复杂度与训练数据集中输入的变化密切相关:数据集中包含的数据点的变 化范围越大,在不发生过拟合的前提下你可以使用的模型就越复杂。通常来说,收集更多 的数据点可以有更大的变化范围,所以更大的数据集可以用来构建更复杂的模型。但是, 仅复制相同的数据点或收集非常相似的数据是无济于事的。
收集更多数据,适当构建更复杂的模型,对监督学习任务往往特别有用。本书主要关注固 定大小的数据集。在现实世界中,你往往能够决定收集多少数据,这可能比模型调参更为 有效。永远不要低估更多数据的力量!
一个模拟的二分类数据集示例是 forge 数据集,它有两个特征。下列代码将绘制一个散点 图(图 2-2),将此数据集的所有数据点可视化。图像以第一个特征为 x 轴,第二个特征为 y 轴。正如其他散点图那样,每个数据点对应图像中的一点。每个点的颜色和形状对应其 类别:
# 生成数据集 X, y = mglearn.datasets.make_forge() # 数据集绘图 mglearn.discrete_scatter(X[:, 0], X[:, 1], y) plt.legend(["Class 0", "Class 1"], loc=4) plt.xlabel("First feature") plt.ylabel("Second feature") print("X.shape: {}".format(X.shape))
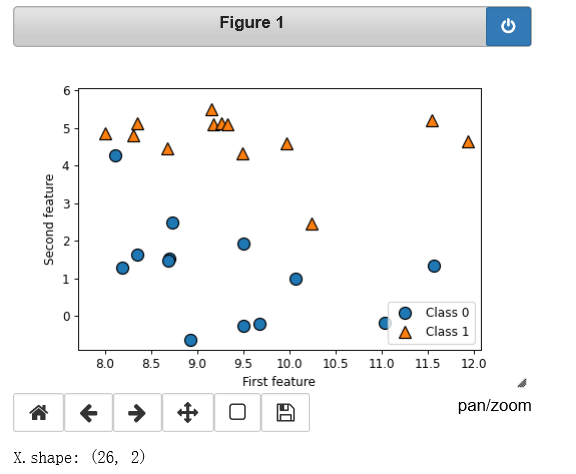
从 X.shape 可以看出,这个数据集包含 26 个数据点和 2 个特征。
我们用模拟的 wave 数据集来说明回归算法。wave 数据集只有一个输入特征和一个连续的 目标变量(或响应),后者是模型想要预测的对象。下面绘制的图像(图 2-3)中单一特征 位于 x 轴,回归目标(输出)位于 y 轴:
X, y = mglearn.datasets.make_wave(n_samples=40) plt.plot(X, y, 'o') plt.ylim(-3, 3) plt.xlabel("Feature") plt.ylabel("Target")
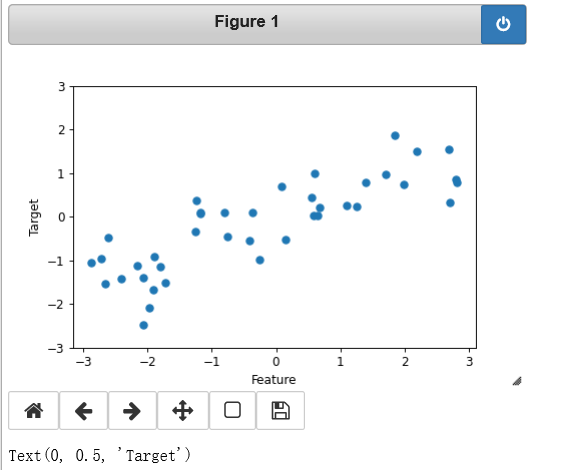
wave 数据集的图像,x轴表示特征,y轴表示回归目标。
我们之所以使用这些非常简单的低维数据集,是因为它们的可视化非常简单——书页只有 两个维度,所以很难展示特征数超过两个的数据。从特征较少的数据集(也叫低维数据 集)中得出的结论可能并不适用于特征较多的数据集(也叫高维数据集)。只要你记住这 一点,那么在低维数据集上研究算法也是很有启发的。
k近邻
k近邻分类
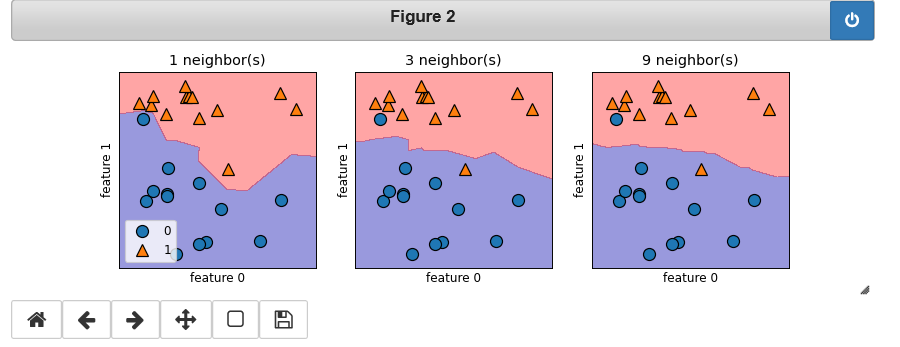
对于二维数据集,我们还可以在 xy 平面上画出所有可能的测试点的预测结果。我们根据 平面中每个点所属的类别对平面进行着色。这样可以查看决策边界(decision boundary), 即算法对类别 0 和类别 1 的分界线。
fig, axes = plt.subplots(1, 3, figsize=(10, 3)) for n_neighbors, ax in zip([1, 3, 9], axes): # fit方法返回对象本身,所以我们可以将实例化和拟合放在一行代码中 clf = KNeighborsClassifier(n_neighbors=n_neighbors).fit(X, y) mglearn.plots.plot_2d_separator(clf, X, fill=True, eps=0.5, ax=ax, alpha=.4) mglearn.discrete_scatter(X[:, 0], X[:, 1], y, ax=ax) ax.set_title("{} neighbor(s)".format(n_neighbors)) ax.set_xlabel("feature 0") ax.set_ylabel("feature 1") axes[0].legend(loc=3)
k近邻回归
%matplotlib notebook from sklearn.neighbors import KNeighborsRegressor X, y = mglearn.datasets.make_wave(n_samples=40) # 将wave数据集分为训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) # 模型实例化,并将邻居个数设为3 reg = KNeighborsRegressor(n_neighbors=3) # 利用训练数据和训练目标值来拟合模型 reg.fit(X_train, y_train) fig, axes = plt.subplots(1, 3, figsize=(15, 4)) # 创建1000个数据点,在-3和3之间均匀分布 line = np.linspace(-3, 3, 1000).reshape(-1, 1) for n_neighbors, ax in zip([1, 3, 9], axes): # 利用1个、3个或9个邻居分别进行预测 reg = KNeighborsRegressor(n_neighbors=n_neighbors) reg.fit(X_train, y_train) ax.plot(line, reg.predict(line)) ax.plot(X_train, y_train, '^', c=mglearn.cm2(0), markersize=8) ax.plot(X_test, y_test, 'v', c=mglearn.cm2(1), markersize=8) ax.set_title( "{} neighbor(s)\n train score: {:.2f} test score: {:.2f}".format( n_neighbors, reg.score(X_train, y_train), reg.score(X_test, y_test))) ax.set_xlabel("Feature") ax.set_ylabel("Target") axes[0].legend(["Model predictions", "Training data/target", "Test data/target"], loc="best")
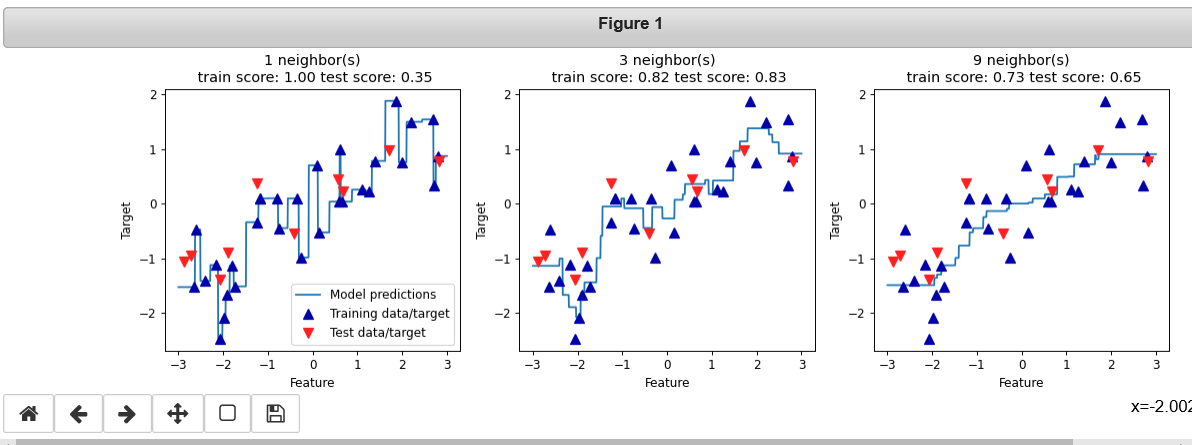
从图中可以看出,仅使用单一邻居,训练集中的每个点都对预测结果有显著影响,预测结 果的图像经过所有数据点。这导致预测结果非常不稳定。考虑更多的邻居之后,预测结果 变得更加平滑,但对训练数据的拟合也不好。一般来说,KNeighbors 分类器有 2 个重要参数:邻居个数与数据点之间距离的度量方法。 在实践中,使用较小的邻居个数(比如 3 个或 5 个)往往可以得到比较好的结果,但你应 该调节这个参数。
虽然 k 近邻算法很容易理解,但由于预测速度慢且不能处理具有很多特征的数据集,所以 在实践中往往不会用到。



