Nearest Common Ancestors
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 26852 | Accepted: 13839 |
Description
A rooted tree is a well-known data structure in computer science and engineering. An example is shown below:
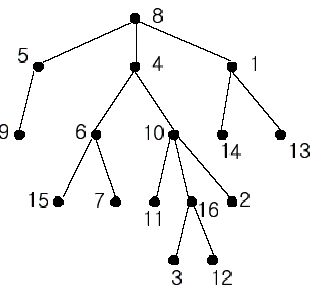
In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.
For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.
Write a program that finds the nearest common ancestor of two distinct nodes in a tree.

In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.
For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.
Write a program that finds the nearest common ancestor of two distinct nodes in a tree.
Input
The input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case starts with a line containing an integer N , the number of nodes in a tree, 2<=N<=10,000. The nodes are labeled with integers 1, 2,..., N. Each of the next N -1 lines contains a pair of integers that represent an edge --the first integer is the parent node of the second integer. Note that a tree with N nodes has exactly N - 1 edges. The last line of each test case contains two distinct integers whose nearest common ancestor is to be computed.
Output
Print exactly one line for each test case. The line should contain the integer that is the nearest common ancestor.
Sample Input
2 16 1 14 8 5 10 16 5 9 4 6 8 4 4 10 1 13 6 15 10 11 6 7 10 2 16 3 8 1 16 12 16 7 5 2 3 3 4 3 1 1 5 3 5
Sample Output
4 3
Source
刚准备练下tarjan的LCA发现这题已经做过了,还是用倍增做的,不错不错
1 #include <cstdio> 2 #include <cmath> 3 #include <cstdlib> 4 #include <cstring> 5 #include <queue> 6 #include <stack> 7 #include <vector> 8 #include <iostream> 9 #include "algorithm" 10 using namespace std; 11 typedef long long LL; 12 const int MAX=10005; 13 int n; 14 int tot; 15 int head[MAX],adj[MAX],next[MAX]; 16 int d[MAX][15]; 17 int father[MAX],deep[MAX]; 18 int root,x,y; 19 void addedge(int u,int v){ 20 tot++; 21 adj[tot]=v; 22 next[tot]=head[u]; 23 head[u]=tot; 24 } 25 void init(){ 26 int i,j; 27 int u,v,w; 28 memset(head,0,sizeof(head)); 29 memset(adj,0,sizeof(adj)); 30 memset(next,0,sizeof(next)); 31 memset(d,0,sizeof(d)); 32 memset(father,0,sizeof(father)); 33 memset(deep,0,sizeof(deep)); 34 scanf("%d",&n); 35 tot=0; 36 int num[MAX]; 37 memset(num,0,sizeof(num)); 38 for (i=1;i<n;i++) 39 {scanf("%d%d",&u,&v); 40 addedge(u,v); 41 //addedge(v,u); 42 num[v]++; 43 } 44 for (i=1;i<=n;i++) 45 if (num[i]==0) 46 {root=i; 47 break; 48 } 49 scanf("%d%d",&x,&y); 50 deep[root]=0; 51 } 52 void bfs(){ 53 int i,j; 54 deep[root]=1; 55 father[root]=0; 56 queue <int> q; 57 q.push(root); 58 while (!q.empty()) 59 {int a; 60 a=q.front(); 61 q.pop(); 62 for (i=head[a];i;i=next[i]) 63 {if (adj[i]==a) 64 continue; 65 deep[adj[i]]=deep[a]+1; 66 father[adj[i]]=a; 67 q.push(adj[i]); 68 } 69 } 70 } 71 int calc(int a){ 72 int i; 73 i=0; 74 while (a) 75 {i++; 76 a/=2; 77 } 78 return i; 79 } 80 int LCA(int x,int y){ 81 int i,j,k; 82 bfs(); 83 for (i=1;i<=n;i++) 84 d[i][0]=father[i]; 85 int maxlogn(calc(n)); 86 for (j=1;j<=maxlogn;j++) 87 for (i=1;i<=n;i++) 88 d[i][j]=d[d[i][j-1]][j-1]; 89 if (deep[x]<deep[y]) 90 swap(x,y); 91 for (i=maxlogn;i>=0;i--) 92 if (deep[y]<=deep[d[x][i]]) 93 x=d[x][i]; 94 if (x==y) 95 return x; 96 for (i=maxlogn;i>=0;i--) 97 if (d[x][i]!=d[y][i]) 98 {x=d[x][i]; 99 y=d[y][i]; 100 } 101 return father[x]; 102 } 103 int main(){ 104 freopen ("LCA.in","r",stdin); 105 freopen ("LCA.out","w",stdout); 106 int i,j; 107 int t; 108 scanf("%d",&t); 109 while (t--) 110 {init(); 111 printf("%d\n",LCA(x,y)); 112 } 113 return 0; 114 }
未来是什么样,未来会发生什么,谁也不知道。
但是我知道,
起码从今天开始努力,
肯定比从明天开始努力,
要快一天实现梦想。
千里之行,始于足下! ——《那年那兔那些事儿》





【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步