MATLAB一元线性回归分析应用举例
作者:凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/
huigui.m
function [b,bint,r,rint,states,sima2,p,y0,zxqj]=huigui(x,y,x0) %x –p元线性模型自变量的n个观测值的n×p矩阵,y -p元线性模型因变量的n个观测值的n×1向量,x0为预测值的横坐标 %b -模型系数β的最小二乘估计值,bint -模型系数β的100(1-alpha)%置信区间,r -模型拟合残差,rint -模型拟合残差的100(1-alpha)%置信区间. %stats -包含R^2统计量、方差分析的F统计量的值、方差分析的显著性概率p值和sigama^2的估计值,y0为预测值纵坐标 format short; x1=[ones(length(x),1),x]; [b,bint,r,rint,states]=regress(y,x1); sima2=(vpa(states(4),20)); p=vpa(states(3),20); %检验的p值 p<0.01,回归方程高度显著;0.0.1<=p<0.05,回归方程显著;p>=0.05,回归方程不显著 y0=b(1)+b(2)*x0; s=sqrt(states(4)); zxqj=[y0-2*s,y0+2*s]; %置信区间 plot(x,y,'.'),lsline %rcoplot(r,rint) %残差分析
结果:
>> x=[1,2,3,4,5,6,7,8,9]'; >> y=[2,4,6,8,10,11,14,16,18]'; >> x0=10; >> [b,bint,r,rint,states,sima2,p,y0,zxqj]=huigui(x,y,x0) b = -0.0278 1.9833 bint = -0.6342 0.5786 1.8756 2.0911 r = 0.0444 0.0611 0.0778 0.0944 0.1111 -0.8722 0.1444 0.1611 0.1778 rint = -0.6654 0.7543 -0.7116 0.8338 -0.7363 0.8918 -0.7426 0.9315 -0.7321 0.9543 -0.8722 -0.8722 -0.6611 0.9500 -0.5981 0.9203 -0.5124 0.8679 states = 1.0e+03 * 0.0010 1.8941 0.0000 0.0001 sima2 = 0.12460317460317460317 p = 0.00000000088276169535500757861 y0 = 19.8056 zxqj = 19.0996 20.5115
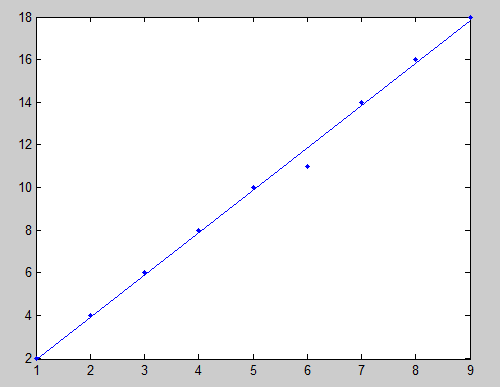
残差图: