凯鲁嘎吉 - 博客园
http://www.cnblogs.com/kailugaji/
某糖果厂用原料A、B和C按不向比率混合加工而成甲、乙、丙三种糖果(假设混合加工中不损耗原料)。原料A、B、C在糖果甲、乙、丙中的含量、原料成本、加工成本、原料限量及糖果售价如表所示。
问该厂对这三种糖果各生产多少公斤，使得到的利润最大?
|
含量(%) |
j号糖果 |
原料供应量 ai(公斤) |
成本(元／公斤) |
|||
|
甲(1号) |
乙(2号) |
丙(3号) |
||||
|
i号原料 |
A(1号)
|
≥60％
|
≥15％
|
|
2000
|
2.50
|
|
B(2号)
|
|
|
|
2500
|
2.00
|
|
|
C(3号)
|
≤20％
|
≤60％
|
≤70％
|
2200
|
1.70
|
|
|
加工成本(元／公斤)
|
2.00
|
1.80
|
1.60
|
|
|
|
|
售价(元／公斤)
|
12
|
10
|
8
|
|
||
解:设i号原料在j号糖果中的用量为xij公斤。
显然，j号糖果的产量为x1j+x2j+x3j
根据原料供应量情况，有约束条件
xi1+xi2+xi3≤ai i=1，2，3。
根据各种原料在各类糖果中的含量要求，有约束条件：
x11≥0.6(x11+x2l+x31)
x3l≤0.2(xll+x2l+x31)
x12≥0.15(x12+x12+x32)
x32≤0.6(x12+x22+x32)
x33≤0.7(x13+x23+x33)
又知原料成本为
糖果加工成本为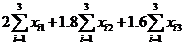
糖果出售收入为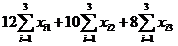
经过整理，本问题的线性规划模型为
max=10*(x11+x21+x31)+8.2*(x12+x22+x32)+6.4*(x13+x23+x33)-2.5*(x11+x12+x13)-2*(x21+x22+x23)-1.7*(x31+x32+x33); x11>0.6*(x11+x21+x31); x12>0.15*(x12+x22+x32); x31<0.2*(x21+x31+x11); x32<0.6*(x12+x22+x32); x33<0.7*(x13+x23+x33); x11+x12+x13<2000; x21+x22+x23<2500; x31+x32+x33<2200; y1=x11+x21+x31; y2=x12+x22+x32; y3=x13+x23+x33; end
结果为：
Global optimal solution found. Objective value: 45180.00 Infeasibilities: 0.000000 Total solver iterations: 5 Variable Value Reduced Cost X11 1326.667 0.000000 X21 442.2222 0.000000 X31 442.2222 0.000000 X12 673.3333 0.000000 X22 2057.778 0.000000 X32 1757.778 0.000000 X13 0.000000 5.200000 X23 0.000000 1.200000 X33 0.000000 1.200000 Y1 2211.111 0.000000 Y2 4488.889 0.000000 Y3 0.000000 0.000000 Row Slack or Surplus Dual Price 1 45180.00 1.000000 2 0.000000 -4.000000 3 0.000000 -4.000000 4 0.000000 0.000000 5 935.5556 0.000000 6 0.000000 0.000000 7 0.000000 9.100000 8 0.000000 5.600000 9 0.000000 5.900000 10 0.000000 0.000000 11 0.000000 0.000000 12 0.000000 0.000000
