The Cross-Entropy Loss Function for the Softmax Function
作者：凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/
本文介绍含有softmax函数的交叉熵损失函数的求导过程，并介绍一种交叉熵损失的等价形式，从而解决因log(0)而出现数值为NaN的问题。
1. softmax函数求导
2. 交叉熵损失求导(含softmax)
3. 交叉熵损失函数(含softmax函数)的等价形式
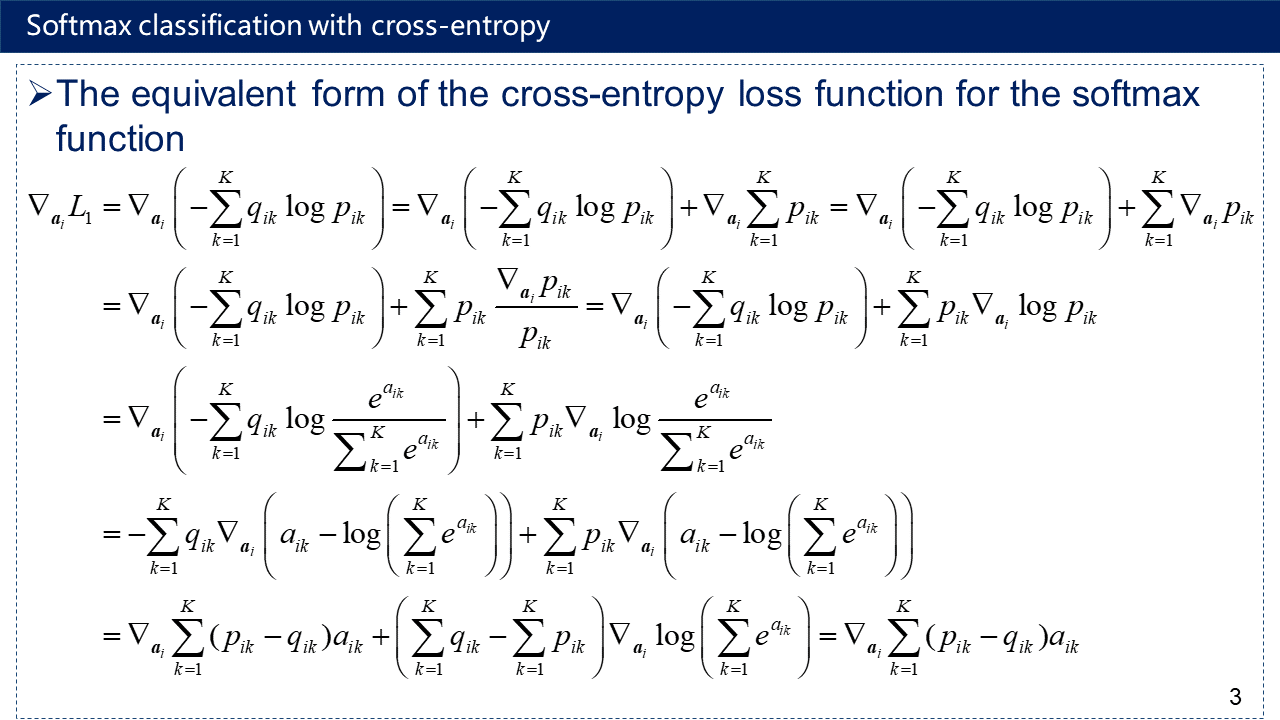
4. Python验证${p_i}\left( {{a_i} - \sum\limits_{j = 1}^K {{p_{ij}}{a_{ij}}} } \right) = 0$
1 # -*- coding: utf-8 -*- 2 # Author：凯鲁嘎吉 Coral Gajic 3 # https://www.cnblogs.com/kailugaji/ 4 # 验证E(X-EX)=0 5 import numpy as np 6 a = np.random.rand(5) 7 p = np.random.rand(5) 8 p = p / p.sum(axis=0, keepdims=True) 9 b = (np.dot(p, a)).sum() 10 print('a: ', a) 11 print('p: ', p) 12 print('b: ', b) 13 print('结果: ', (p * (a - b)).sum())
结果：
D:\ProgramData\Anaconda3\python.exe "D:/Python code/2023.3 exercise/向量间的距离度量/test.py" a: [0.90457897 0.08975555 0.6955031 0.74161145 0.50095907] p: [0.02797057 0.09509987 0.27454503 0.273575 0.32880953] b: 0.5923907183986392 结果: 5.204170427930421e-17 Process finished with exit code 0
5. Python验证$L_1$与$L_2$等价
1 # -*- coding: utf-8 -*- 2 # Author：凯鲁嘎吉 Coral Gajic 3 # https://www.cnblogs.com/kailugaji/ 4 # Softmax classification with cross-entropy 5 import torch 6 import numpy as np 7 import matplotlib.pyplot as plt 8 plt.rc('font',family='Times New Roman') 9 10 def sinkhorn(scores, eps = 5.0, n_iter = 3): 11 def remove_infs(x): 12 mm = x[torch.isfinite(x)].max().item() 13 x[torch.isinf(x)] = mm 14 x[x==0] = 1e-38 15 return x 16 scores = torch.tensor(scores) 17 n, m = scores.shape 18 scores1 = scores.view(n*m) 19 Q = torch.softmax(-scores1/eps, dim=0) 20 Q = remove_infs(Q).view(n,m).T 21 r, c = torch.ones(n), torch.ones(m) * (n / m) 22 for _ in range(n_iter): 23 u = (c/torch.sum(Q, dim=1)) 24 Q *= remove_infs(u).unsqueeze(1) 25 v = (r/torch.sum(Q,dim=0)) 26 Q *= remove_infs(v).unsqueeze(0) 27 bsum = torch.sum(Q, dim=0, keepdim=True) 28 Q = Q / remove_infs(bsum) 29 P = Q.T 30 assert torch.isnan(P.sum())==False 31 return P 32 33 n = 128 34 m = 64 35 loss_1 = [] 36 loss_2 = [] 37 for _ in range(20): 38 a = torch.rand(n, m) 39 a = a ** 4 40 a = a / a.sum(dim = -1, keepdim = True) 41 P = torch.softmax(a, dim=1) 42 b = np.random.rand(n, m) 43 b = b ** 1.5 44 Q = sinkhorn(b, 0.5, 10) 45 # 方法1： 46 loss_11 = -(Q * torch.log(P)).sum(-1).mean() 47 loss_1.append(loss_11) 48 # 方法2： 49 loss_22 = ((P - Q) * a).sum(-1).mean() 50 loss_2.append(loss_22) 51 52 loss_1, index = torch.sort(torch.tensor(loss_1), 0) 53 loss_2 = np.array(loss_2)[index] 54 print('方法1--损失：\n', np.array(loss_1)) 55 print('方法2--损失：\n', loss_2) 56 grad_1 = np.gradient(np.array(loss_1)) 57 grad_2 = np.gradient(np.array(loss_2)) 58 print('方法1--梯度：\n', np.array(grad_1)) 59 print('方法2--梯度：\n', np.array(grad_2)) 60 plt.subplots(1, 2, figsize=(16, 7)) 61 plt.subplot(1, 2, 1) 62 plt.plot(loss_1, loss_2, color = 'red', ls = '-') 63 plt.xlabel('Loss 1') 64 plt.ylabel('Loss 2') 65 plt.subplot(1, 2, 2) 66 plt.scatter(grad_1*1E6, grad_2*1E6, color = 'blue') 67 plt.xlabel('Gradient 1') 68 plt.ylabel('Gradient 2') 69 plt.savefig('softmax cross-entropy loss.png', bbox_inches='tight', dpi=500) 70 plt.show()
结果：
D:\ProgramData\Anaconda3\python.exe "D:/Python code/2023.3 exercise/向量间的距离度量/softmax_cross_entropy_loss_test.py" 方法1--损失： [4.15883989 4.15890663 4.15894403 4.15897117 4.15902341 4.15904347 4.1590823 4.1590913 4.15910622 4.15913114 4.15913474 4.1591434 4.15914856 4.15916808 4.15916826 4.15917904 4.15918445 4.15918608 4.15925961 4.15926385] 方法2--损失： [0.00017298 0.00024753 0.00028277 0.00030974 0.00036783 0.0003804 0.00041808 0.00043415 0.00044729 0.00047444 0.00047943 0.00048301 0.00049451 0.00050864 0.00051069 0.0005161 0.00053111 0.00052533 0.00060765 0.0006024 ] 方法1--梯度： [6.67441917e-05 5.20709542e-05 3.22701985e-05 3.96937794e-05 3.61504422e-05 2.94408723e-05 2.39134622e-05 1.19608872e-05 1.99222036e-05 1.42617498e-05 6.12662792e-06 6.90728703e-06 1.23429982e-05 9.85375545e-06 5.47883732e-06 8.09470613e-06 3.52000565e-06 3.75770611e-05 3.88866185e-05 4.24487449e-06] 方法2--梯度： [ 7.45563606e-05 5.48997609e-05 3.11016626e-05 4.25261140e-05 3.53301332e-05 2.51239797e-05 2.68772106e-05 1.46074152e-05 2.01447210e-05 1.60698704e-05 4.28303591e-06 7.54056029e-06 1.28157065e-05 8.08914041e-06 3.73246714e-06 1.02123578e-05 4.61507539e-06 3.82697805e-05 3.85335993e-05 -5.25437451e-06] Process finished with exit code 0
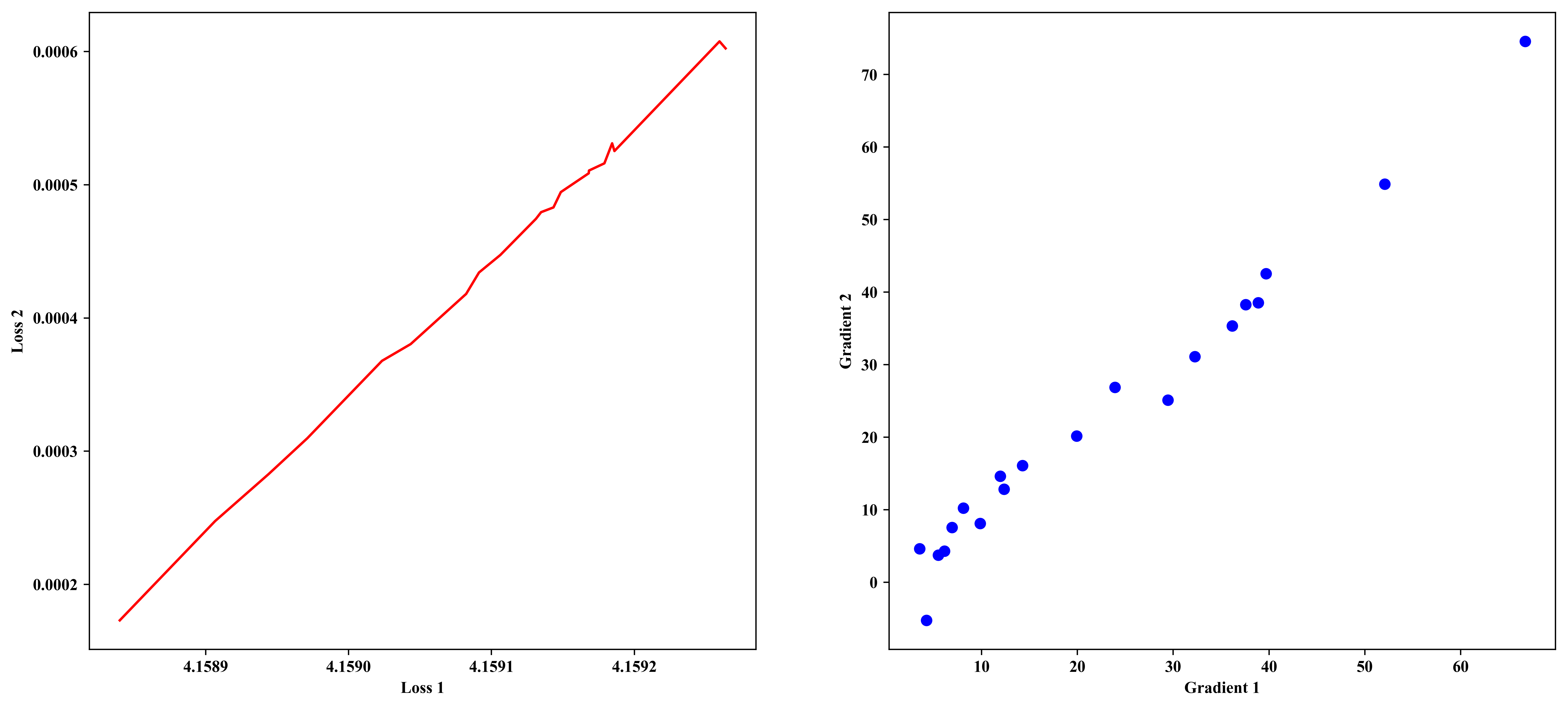
可以看到，虽然理论上可以证明$L_1$与$L_2$的梯度相等，但实际应用时还是有点偏颇，当数据量与数据维度足够大时，$L_1$与$L_2$的数值呈现线性相关。
6. 参考文献
[1] Softmax classification with cross-entropy (2/2)
[2] Liu Q, Zhou Q, Yang R, et al. Robust Representation Learning by Clustering with Bisimulation Metrics for Visual Reinforcement Learning with Distractions[C]. AAAI, 2023.
