Python小练习：优化器torch.optim的使用

Python小练习：优化器torch.optim的使用

作者：凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/

本文主要介绍Pytorch中优化器的使用方法，了解optimizer.zero_grad()、loss.backward()以及optimizer.step()函数的用法。

问题陈述：假设最小化目标函数为$L = \sum\nolimits_{i = 1}^N {x_i^2} $。给定初始值$\left[ {x_1^{(0)},x_2^{(0)}} \right] = [5,{\rm{ }}10]$，求最优解$\hat x = \arg \min L$。

1. optim_test.py

# -*- coding: utf-8 -*-
# Author：凯鲁嘎吉 Coral Gajic
# https://www.cnblogs.com/kailugaji/
# Python小练习：优化器torch.optim的使用
# 假设损失函数为loss = ∑(x^2)，给定初始x(0)，目的是找到最优的x，使得loss最小化
# 以2维数据为例，loss = x1^2 + x2^2
# loss对x1的偏导为2 * x1，loss对x2的偏导为2 * x2
'''
部分参考：
    https://www.cnblogs.com/zhouyang209117/p/16048331.html
'''
import torch
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
plt.rc('font',family='Times New Roman')

# 方法一：
# 自己实现的优化
rate = 0.1 # 学习率
iteration = 30 # 迭代次数
num = 3
data = np.array([5.0, 10.0]) # 给定初始数据x(0)
for i in range(iteration):
    loss = (data ** 2).sum(axis = 0) # 优化目标：最小化loss = x1^2 + x2^2
    my_grad = 2 * data # 梯度d(loss)/dx：2 * x1, 2 * x2
    print('%d.' %(i+1),
          '数据：', np.around(data, num),
          '\t损失函数：', np.around(loss, num),
          '\t梯度：', np.around(my_grad, num)
          )
    data -= my_grad * rate # 优化更新：x = x - learning_rate * (d(loss)/dx)

print('----------------------------------------------------------------')
# 方法二：
# pytorch自带的优化器
data = np.array([5.0, 10.0]) # 给定初始数据x(0)
data = torch.tensor(data, requires_grad=True) # 需要求梯度
optimizer = optim.SGD([data], lr = rate) # 优化器：随机梯度下降
plot_loss = []
for i in range(iteration):
    optimizer.zero_grad() # 清空先前的梯度
    loss = (data ** 2).sum() # 优化目标：最小化loss = x1^2 + x2^2
    print('%d.' %(i+1),
          '数据：', np.around(data.detach().numpy(), num),
          '\t损失函数：', np.around(loss.item(), num),
          end=' '
          )
    loss.backward() # 计算当前梯度d(loss)/dx = 2 * x，并反向传播
    print('\t梯度：', np.around(data.grad.detach().numpy(), num)) # 打印梯度
    optimizer.step() # 优化更新：x = x - learning_rate * (d(loss)/dx)
    plot_loss.append([i+1, loss.item()]) # 保存每次迭代的loss

plot_loss = np.array(plot_loss) # 将list转换成numpy
# --------------------画Loss曲线图------------------------
plt.plot(plot_loss[:, 0], plot_loss[:, 1], color = 'red', ls = '-')
plt.xlabel('Iteration')
plt.ylabel('Loss')
plt.tight_layout()
plt.savefig('Loss.png', bbox_inches='tight', dpi=500)
plt.show()

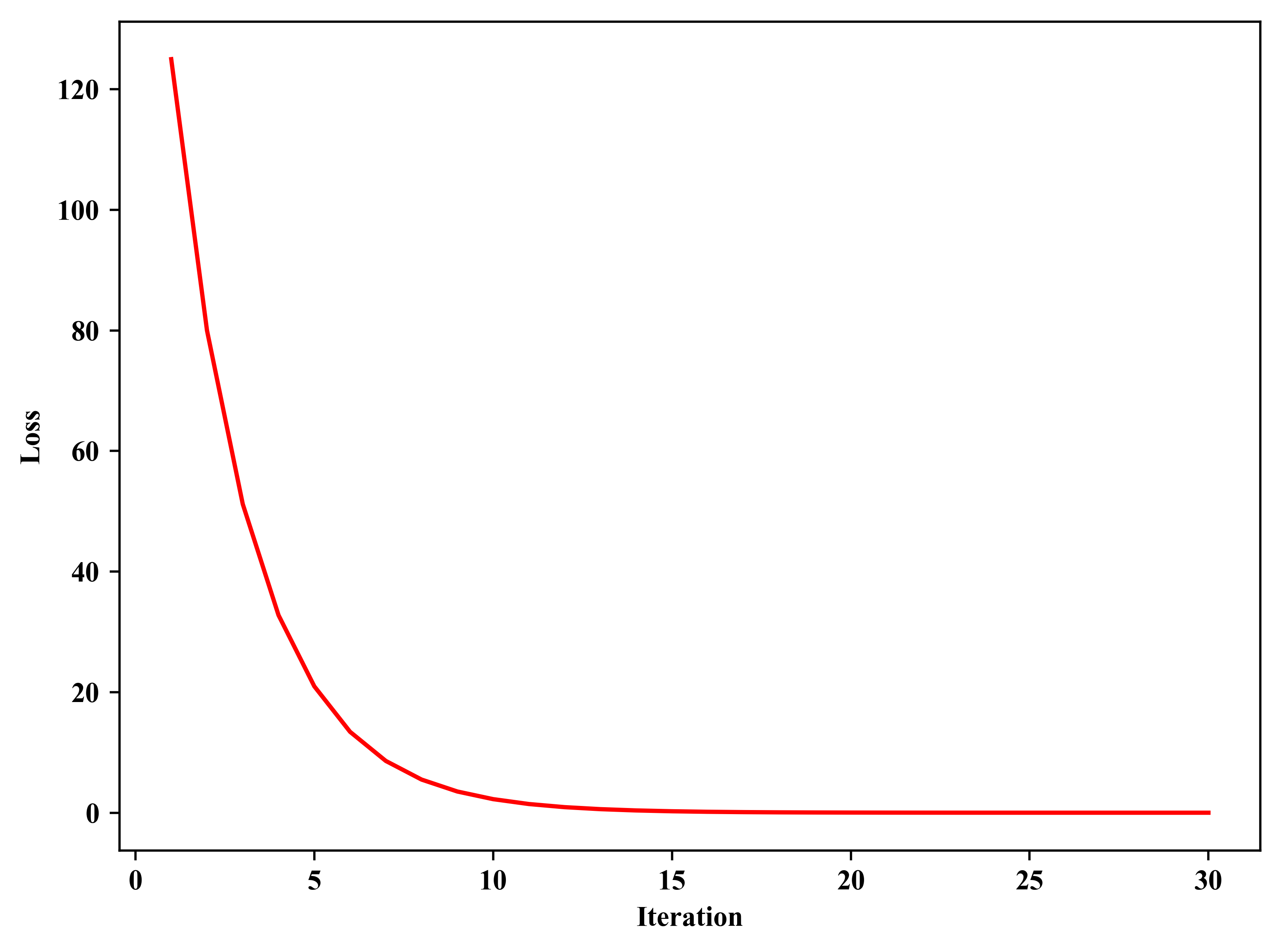
2. 结果

D:\ProgramData\Anaconda3\python.exe "D:/Python code/2023.3 exercise/optimizer/optim_test.py"
1. 数据： [ 5. 10.]     损失函数： 125.0     梯度： [10. 20.]
2. 数据： [4. 8.]     损失函数： 80.0     梯度： [ 8. 16.]
3. 数据： [3.2 6.4]     损失函数： 51.2     梯度： [ 6.4 12.8]
4. 数据： [2.56 5.12]     损失函数： 32.768     梯度： [ 5.12 10.24]
5. 数据： [2.048 4.096]     损失函数： 20.972     梯度： [4.096 8.192]
6. 数据： [1.638 3.277]     损失函数： 13.422     梯度： [3.277 6.554]
7. 数据： [1.311 2.621]     损失函数： 8.59     梯度： [2.621 5.243]
8. 数据： [1.049 2.097]     损失函数： 5.498     梯度： [2.097 4.194]
9. 数据： [0.839 1.678]     损失函数： 3.518     梯度： [1.678 3.355]
10. 数据： [0.671 1.342]     损失函数： 2.252     梯度： [1.342 2.684]
11. 数据： [0.537 1.074]     损失函数： 1.441     梯度： [1.074 2.147]
12. 数据： [0.429 0.859]     损失函数： 0.922     梯度： [0.859 1.718]
13. 数据： [0.344 0.687]     损失函数： 0.59     梯度： [0.687 1.374]
14. 数据： [0.275 0.55 ]     损失函数： 0.378     梯度： [0.55 1.1 ]
15. 数据： [0.22 0.44]     损失函数： 0.242     梯度： [0.44 0.88]
16. 数据： [0.176 0.352]     损失函数： 0.155     梯度： [0.352 0.704]
17. 数据： [0.141 0.281]     损失函数： 0.099     梯度： [0.281 0.563]
18. 数据： [0.113 0.225]     损失函数： 0.063     梯度： [0.225 0.45 ]
19. 数据： [0.09 0.18]     损失函数： 0.041     梯度： [0.18 0.36]
20. 数据： [0.072 0.144]     损失函数： 0.026     梯度： [0.144 0.288]
21. 数据： [0.058 0.115]     损失函数： 0.017     梯度： [0.115 0.231]
22. 数据： [0.046 0.092]     损失函数： 0.011     梯度： [0.092 0.184]
23. 数据： [0.037 0.074]     损失函数： 0.007     梯度： [0.074 0.148]
24. 数据： [0.03  0.059]     损失函数： 0.004     梯度： [0.059 0.118]
25. 数据： [0.024 0.047]     损失函数： 0.003     梯度： [0.047 0.094]
26. 数据： [0.019 0.038]     损失函数： 0.002     梯度： [0.038 0.076]
27. 数据： [0.015 0.03 ]     损失函数： 0.001     梯度： [0.03 0.06]
28. 数据： [0.012 0.024]     损失函数： 0.001     梯度： [0.024 0.048]
29. 数据： [0.01  0.019]     损失函数： 0.0     梯度： [0.019 0.039]
30. 数据： [0.008 0.015]     损失函数： 0.0     梯度： [0.015 0.031]
----------------------------------------------------------------
1. 数据： [ 5. 10.]     损失函数： 125.0     梯度： [10. 20.]
2. 数据： [4. 8.]     损失函数： 80.0     梯度： [ 8. 16.]
3. 数据： [3.2 6.4]     损失函数： 51.2     梯度： [ 6.4 12.8]
4. 数据： [2.56 5.12]     损失函数： 32.768     梯度： [ 5.12 10.24]
5. 数据： [2.048 4.096]     损失函数： 20.972     梯度： [4.096 8.192]
6. 数据： [1.638 3.277]     损失函数： 13.422     梯度： [3.277 6.554]
7. 数据： [1.311 2.621]     损失函数： 8.59     梯度： [2.621 5.243]
8. 数据： [1.049 2.097]     损失函数： 5.498     梯度： [2.097 4.194]
9. 数据： [0.839 1.678]     损失函数： 3.518     梯度： [1.678 3.355]
10. 数据： [0.671 1.342]     损失函数： 2.252     梯度： [1.342 2.684]
11. 数据： [0.537 1.074]     损失函数： 1.441     梯度： [1.074 2.147]
12. 数据： [0.429 0.859]     损失函数： 0.922     梯度： [0.859 1.718]
13. 数据： [0.344 0.687]     损失函数： 0.59     梯度： [0.687 1.374]
14. 数据： [0.275 0.55 ]     损失函数： 0.378     梯度： [0.55 1.1 ]
15. 数据： [0.22 0.44]     损失函数： 0.242     梯度： [0.44 0.88]
16. 数据： [0.176 0.352]     损失函数： 0.155     梯度： [0.352 0.704]
17. 数据： [0.141 0.281]     损失函数： 0.099     梯度： [0.281 0.563]
18. 数据： [0.113 0.225]     损失函数： 0.063     梯度： [0.225 0.45 ]
19. 数据： [0.09 0.18]     损失函数： 0.041     梯度： [0.18 0.36]
20. 数据： [0.072 0.144]     损失函数： 0.026     梯度： [0.144 0.288]
21. 数据： [0.058 0.115]     损失函数： 0.017     梯度： [0.115 0.231]
22. 数据： [0.046 0.092]     损失函数： 0.011     梯度： [0.092 0.184]
23. 数据： [0.037 0.074]     损失函数： 0.007     梯度： [0.074 0.148]
24. 数据： [0.03  0.059]     损失函数： 0.004     梯度： [0.059 0.118]
25. 数据： [0.024 0.047]     损失函数： 0.003     梯度： [0.047 0.094]
26. 数据： [0.019 0.038]     损失函数： 0.002     梯度： [0.038 0.076]
27. 数据： [0.015 0.03 ]     损失函数： 0.001     梯度： [0.03 0.06]
28. 数据： [0.012 0.024]     损失函数： 0.001     梯度： [0.024 0.048]
29. 数据： [0.01  0.019]     损失函数： 0.0     梯度： [0.019 0.039]
30. 数据： [0.008 0.015]     损失函数： 0.0     梯度： [0.015 0.031]

Process finished with exit code 0