Safe RL——Constrained Variational Policy Optimization for Safe Reinforcement Learning (CVPO)
作者:凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/
强化学习可以看作为概率推断问题。通过阅读2022年发表在ICML上的论文《Constrained Variational Policy Optimization for Safe Reinforcement Learning》,并简要做一下阅读笔记。这篇文章将强化学习问题转换为变分推断的思想进行求解,之前写过类似的博文,如RL——Deep Reinforcement Learning amidst Continual/Lifelong Structured Non-Stationarity,思路都是一样的,只是本文这篇CVPO主要是针对安全强化学习而言,因此引入了安全约束,作者将其嵌入在辅助分布q里面,用来限制q的分布范围。文章大体框架是利用类似期望最大化的思想进行求解,在E步,固定θ,求q,而在M步,固定q,求θ。在求解期间也用到了信赖域的思想,类似于信赖域策略优化(Trust Region Policy Optimization, TRPO),将KL散度约束项放到约束条件中,并定义信赖域半径进行求解。本文主要涉及概率统计的相关知识,在看本文之前,可以先阅读相关博文:变分推断与变分自编码器以及最后参考文献中列出的几篇博文。更多有关强化学习的内容,请看随笔分类 - Reinforcement Learning。(补充:阅读这篇文章之前,也可以先看Maximum a Posteriori Policy Optimisation (MPO)算法。本文这篇其实就是在MPO(非参数化版本)的基础上引入了安全约束,原先的约束条件又被进一步转化为用拉格朗日求解,而其他的设置,包括先验等,都和MPO一模一样。其实也可以用参数化的方法,那样的话就不需要M步了,直接将q得到的θ当做待求的θ进行下一步更新就行,这样就和CPO没太大区别了。)
1. Introduction
介绍共轭先验(Conjugate Priors)与常见的共轭先验分布、参数估计、贝叶斯估计、变分推断、Jensen不等式、平均场理论、Fisher信息量、两个高斯分布的交叉熵与KL散度及其推导、论文的研究背景、现有方法存在的问题以及本文的主要贡献。


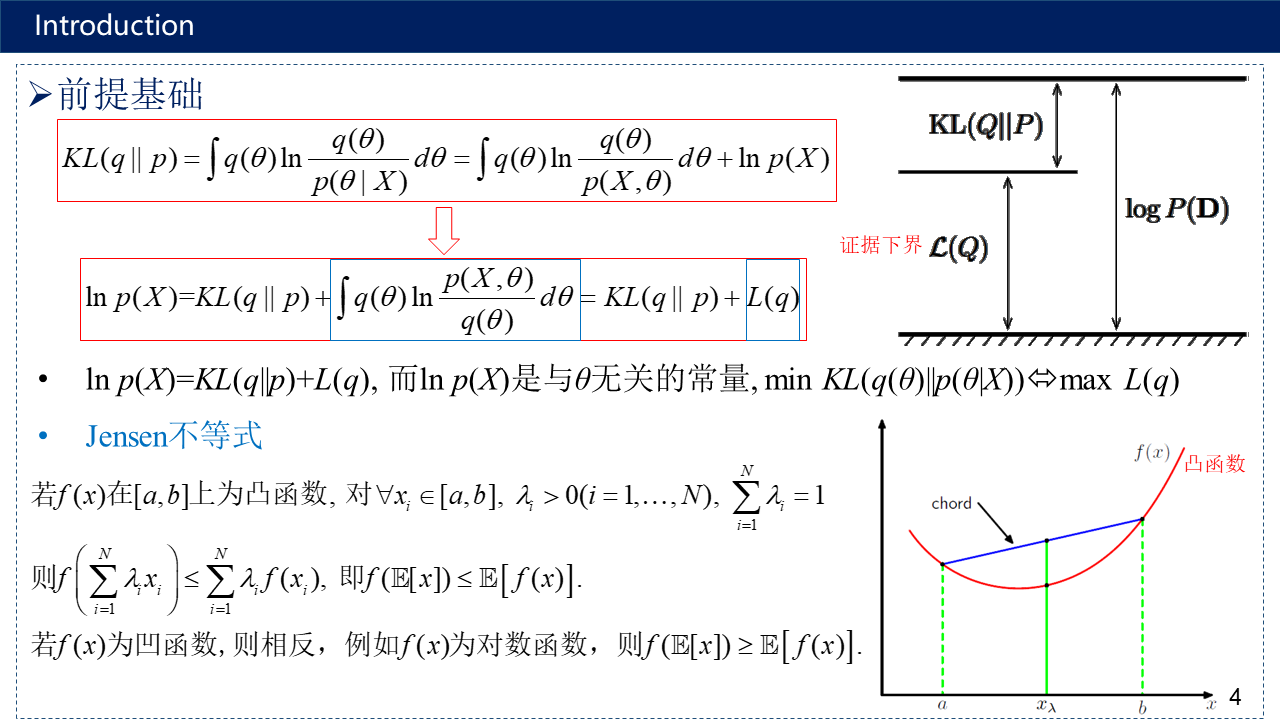



KL散度与Fisher信息量的联系:
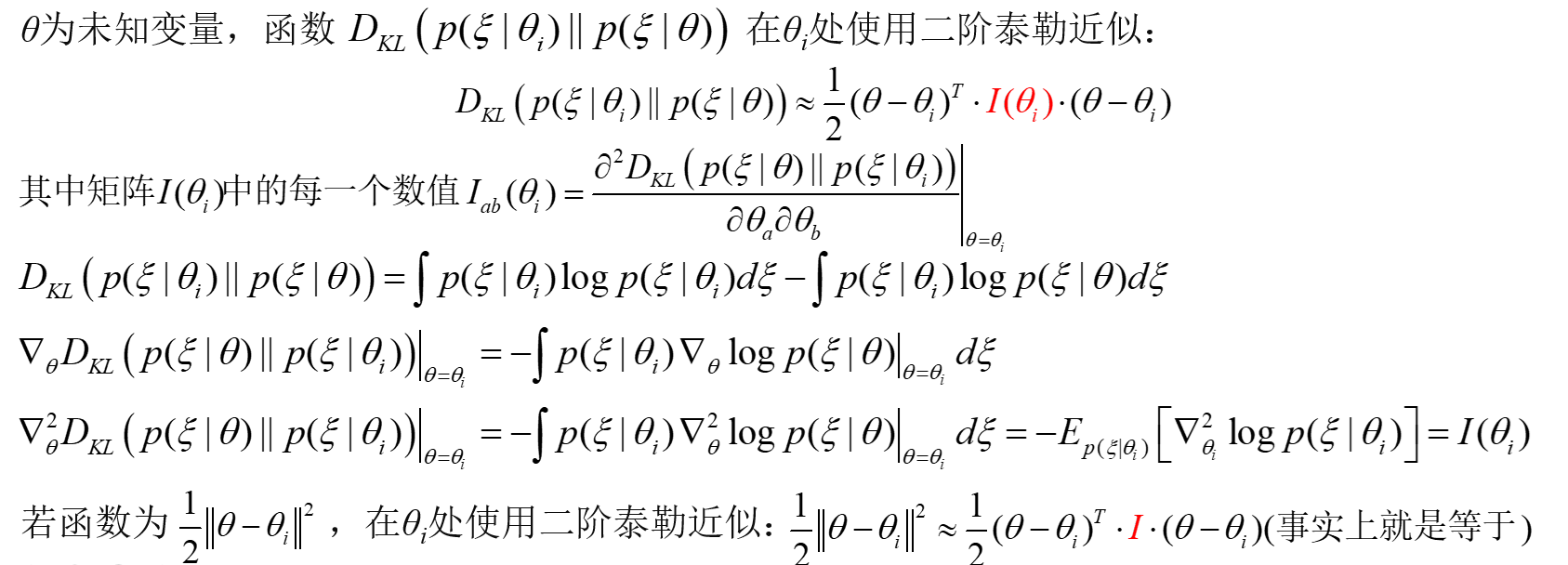





2. Constrained Variational Policy Optimization (CVPO)
主要介绍论文的核心内容,包括Constrained Markov Decision Processes、Primal-Dual View vs Inference View、Constrained RL as Inference、Constrained E-step——固定θ,求q、M-step——固定q,求θ、以及算法流程。


拓展:为什么α会被称为温度参数,这就类比于模拟退火算法,在温度T下,分子停留在状态r满足波尔兹曼概率分布。这里的α就相当于模拟退火中的T。只不过T是一直在变的,而α可能设为固定值。









Critic网络出来的是Q值,和普通的Actor-Critic中的Critic网络一样。



Actor网络出来的是均值与协方差矩阵,而不是直接出来策略的概率。有了均值与协方差矩阵,策略π再根据正态分布的公式计算得出。
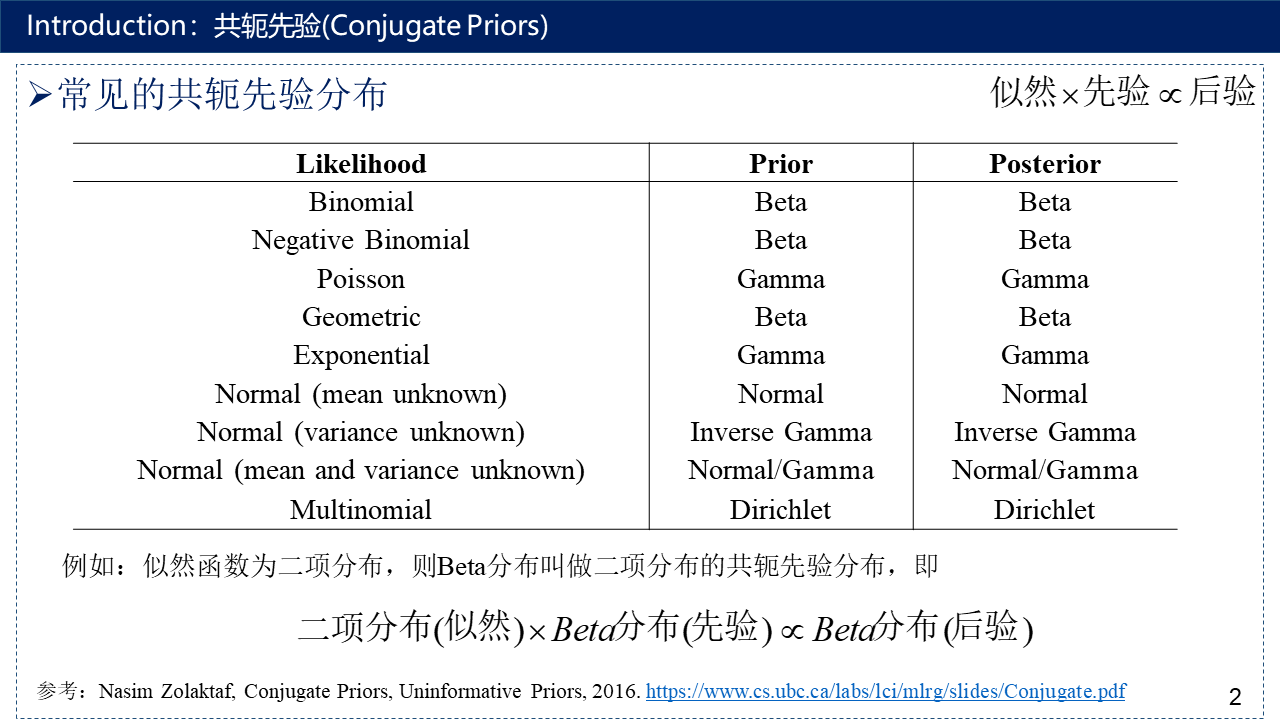
这里面还涉及到一个问题,就是共轭先验(conjugate priors)。由于假设了似然分布${{\pi }_{\theta }}(a|s)$为正态分布,其中均值方差均未知,则其共轭先验分布$p(\theta )$可以为正态分布/Gamma分布,这里为了求解方便,选取了正态分布作为共轭先验。如果似然分布换成了其他的分布形式,相应的先验也应换成与之对应的共轭先验分布。
公式:$p(X|\theta )p(\theta )\propto p(\theta |X)$,即似然函数*先验分布$\propto $后验分布。例如:beta分布叫做二项分布的共轭先验分布,即二项分布*beta分布$\propto $beta分布。


3. Experiments

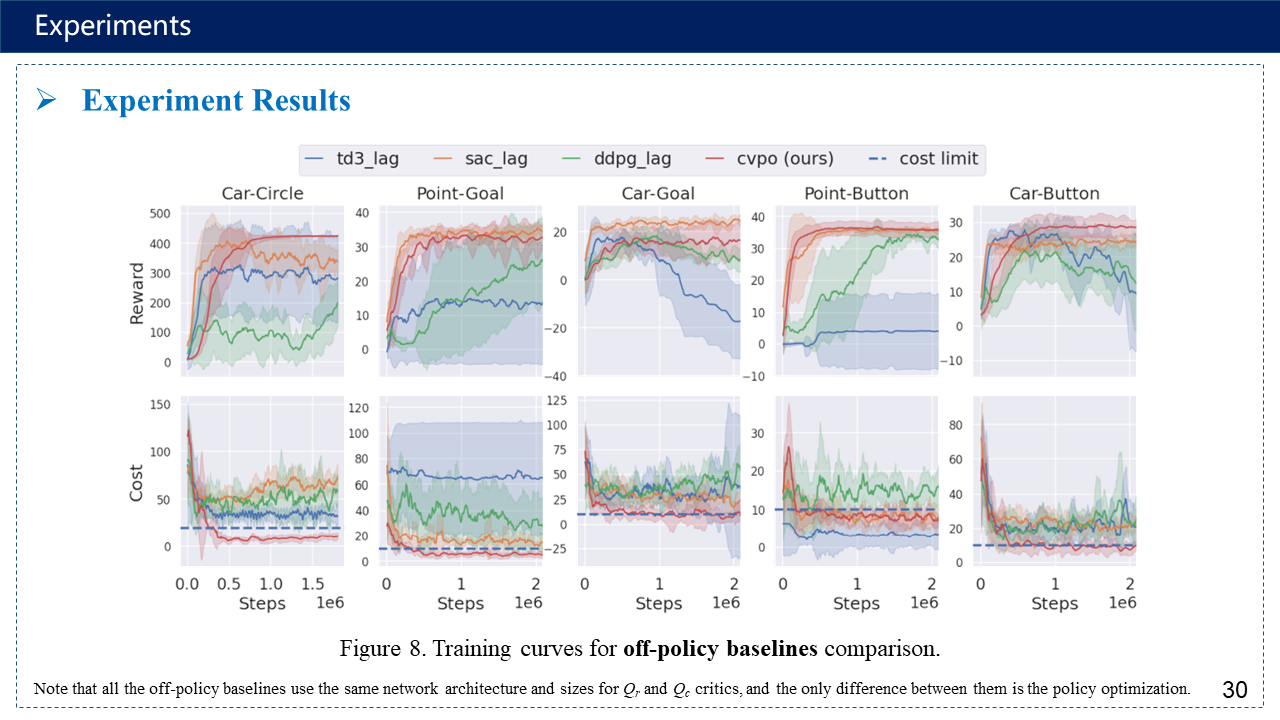
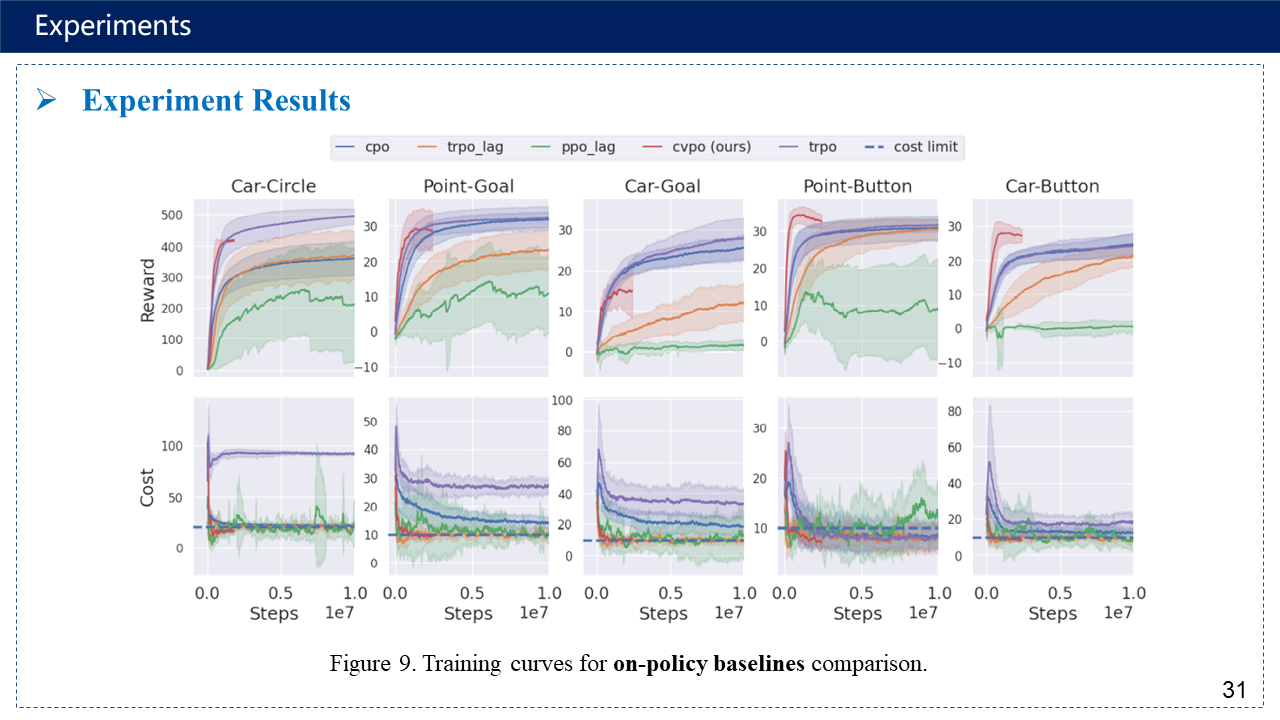
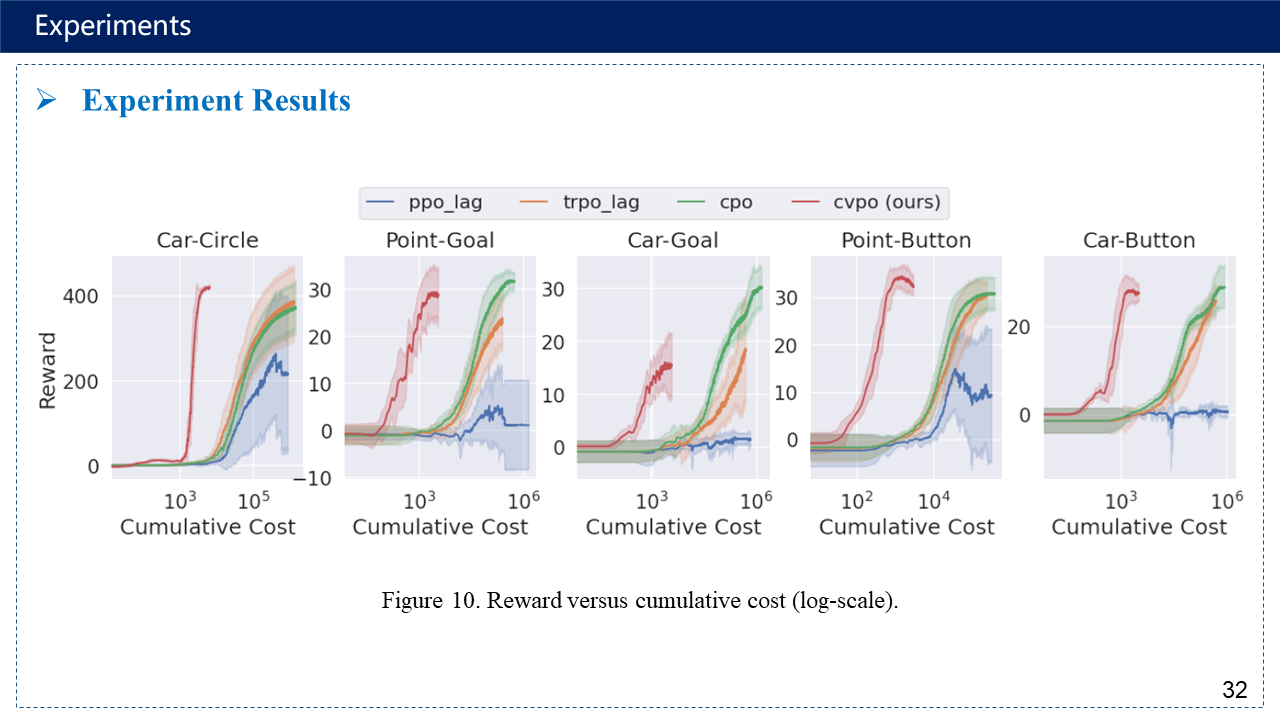
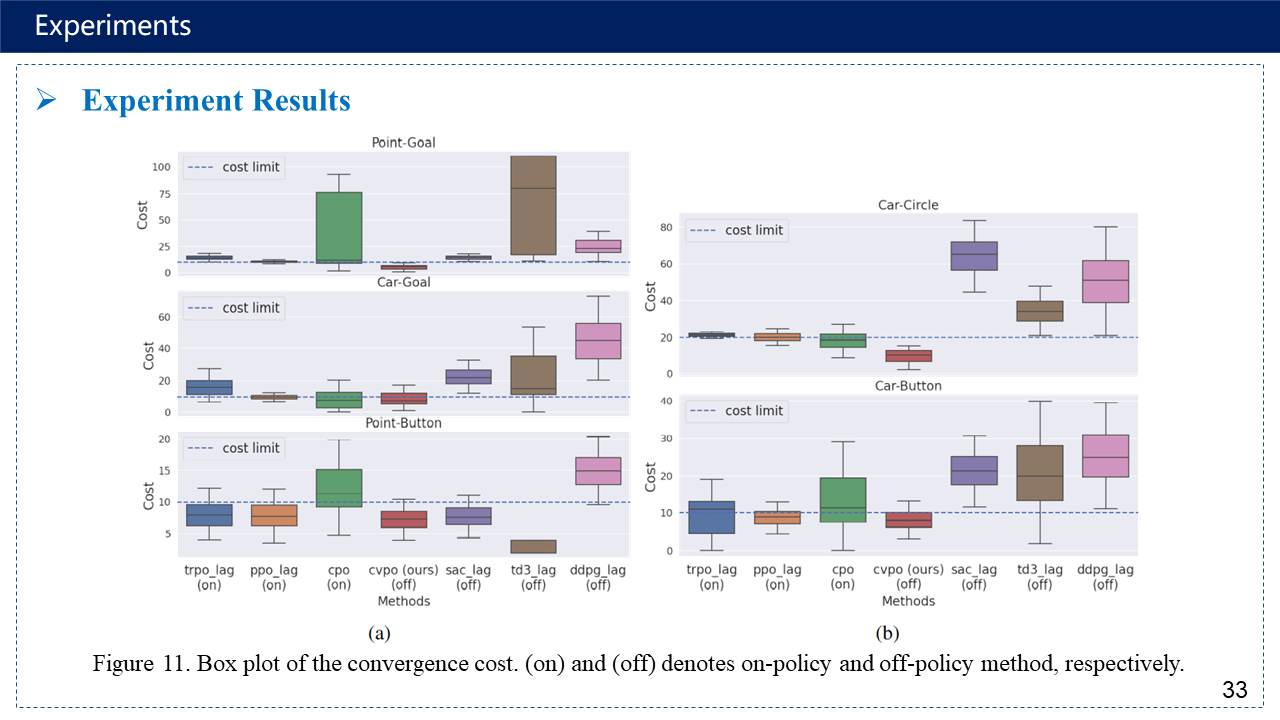
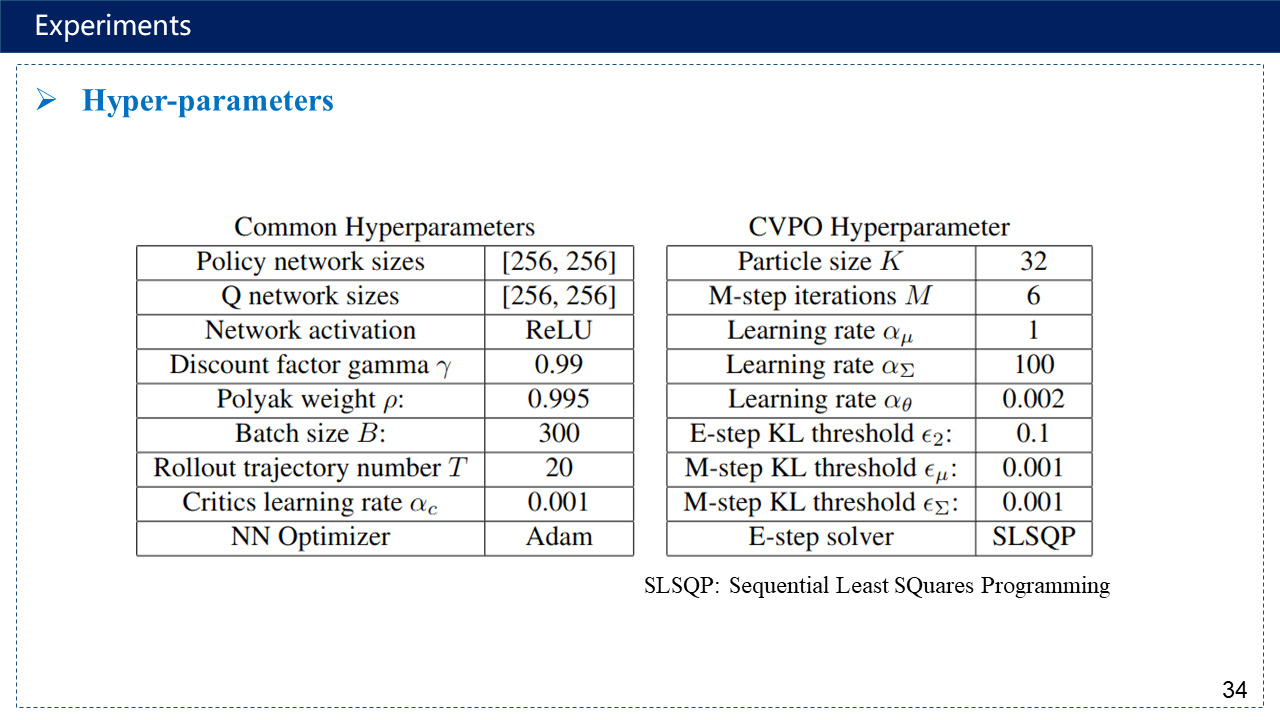
补充:超参数有点多,序列二次规划方法https://www.cnblogs.com/kailugaji/p/16567454.html#_label3_0_4_1
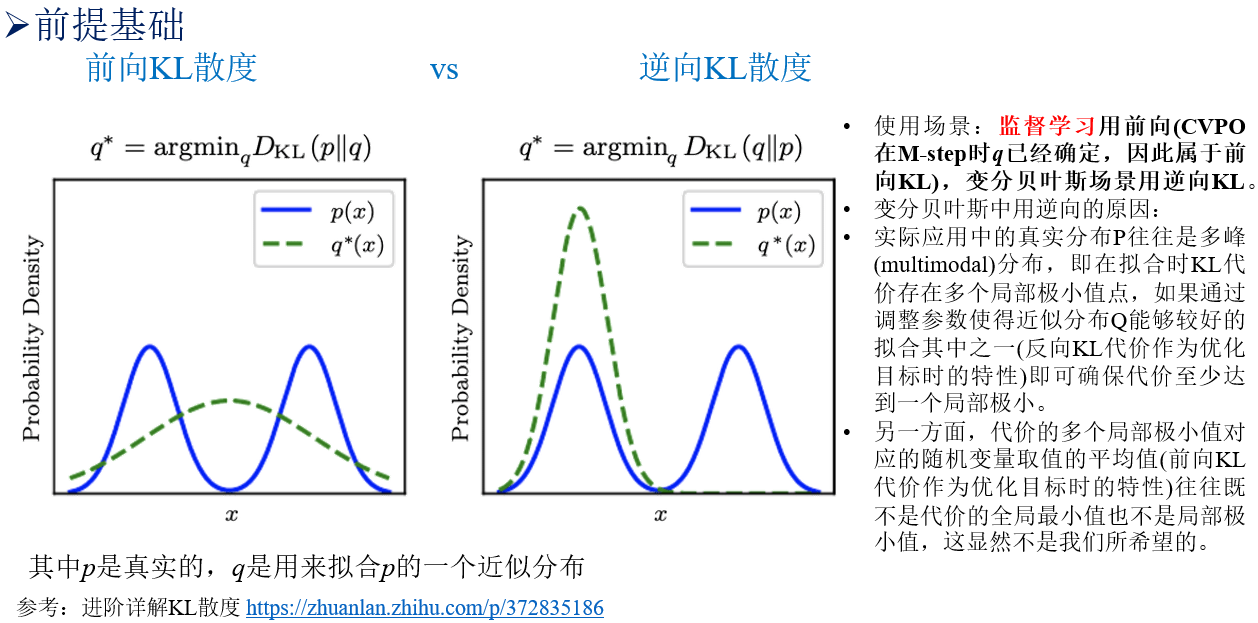
补充:为什么M-step被称为监督学习,这和前向KL与逆向KL散度有关,E-step用的是逆向KL,变分推断经典使用方法,而M-step已知了q之后,相当于用的是前向KL,类似于监督学习。
4. 参考文献
- Zuxin Liu, Zhepeng Cen, Vladislav Isenbaev, Wei Liu, Steven Wu, Bo Li, Ding Zhao. Constrained Variational Policy Optimization for Safe Reinforcement Learning. ICML, 2022.
- Annie Xie, James Harrison, Chelsea Finn. Deep Reinforcement Learning amidst Continual/Lifelong Structured Non-Stationarity. ICML, 2021.
- John S., Sergey L., Pieter A., Michael J., Philipp M., Trust Region Policy Optimization. ICML, 2015. https://www.cnblogs.com/kailugaji/p/15388913.html
- 变分推断与变分自编码器 https://www.cnblogs.com/kailugaji/p/12463966.html
- 变分深度嵌入(Variational Deep Embedding, VaDE) https://www.cnblogs.com/kailugaji/p/12882812.html
- 相关文章:A. Abdolmaleki, J. T. Springenberg, Y. Tassa, et al. Maximum a Posteriori Policy Optimisation. ICLR, 2018.
- Nasim Zolaktaf, Conjugate Priors, Uninformative Priors, 2016. https://www.cs.ubc.ca/labs/lci/mlrg/slides/Conjugate.pdf


 浙公网安备 33010602011771号
浙公网安备 33010602011771号