最优化——约束优化方法(Constrained Optimization Algorithms)
作者：凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/
本篇介绍最优化方法(运筹学)里面的约束优化方法，包括：直接搜索法(随机方向法、约束坐标轮换法、复合形法、以及可行方向法)与间接搜索法(惩罚函数法与序列二次规划)。更多优化问题，请看标签：优化问题 - 凯鲁嘎吉
1. 引言
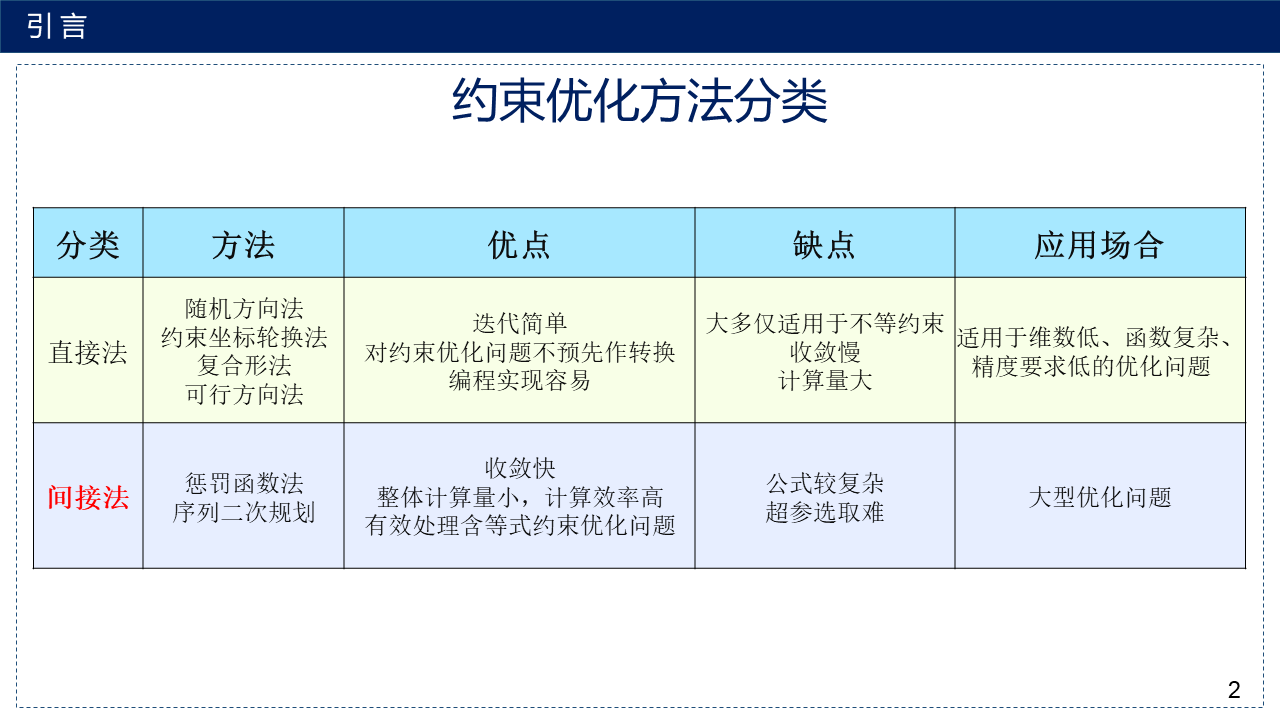
包括约束非线性规划问题陈述、约束优化方法分类、最优性条件。
2. 直接搜索法(Direct Search Methods)
2.1 随机方向法
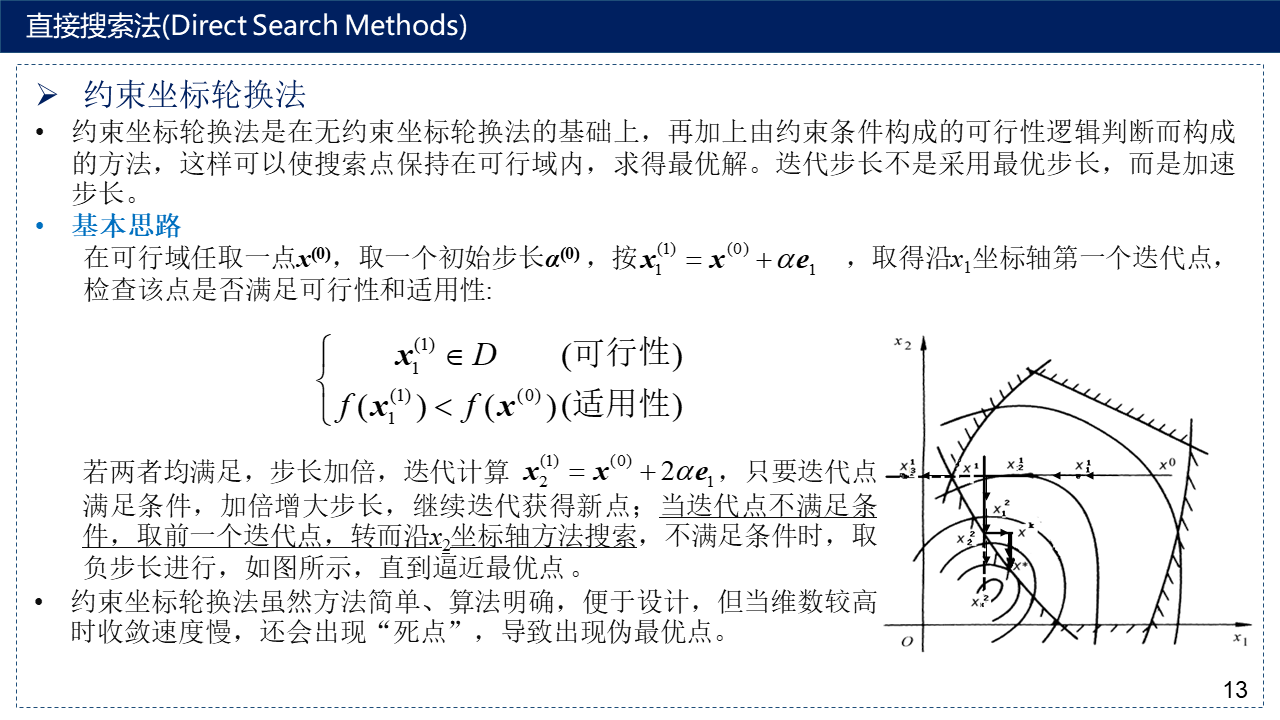
2.2 约束坐标轮换法
2.3 复合形法(complex method)
3. 可行方向法(Feasible Directions Methods)
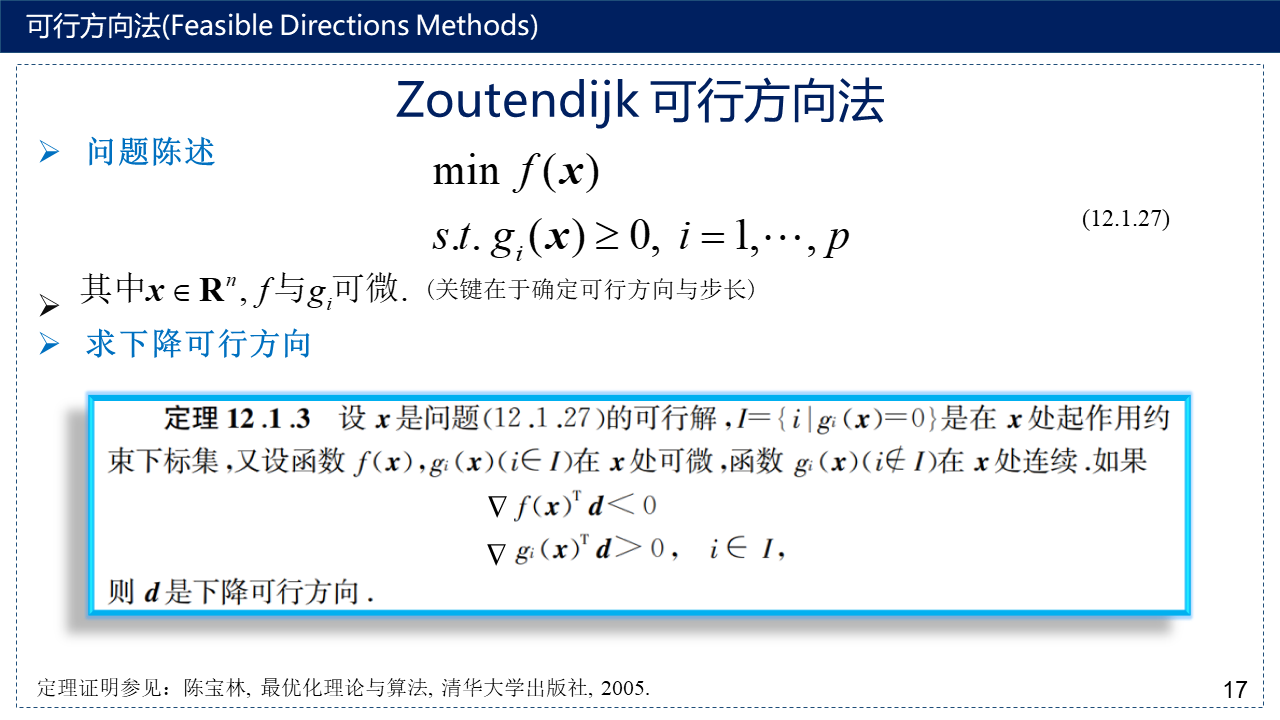
3.1 Zoutendijk可行方向法
3.2 Rosen梯度投影法
3.3 Wolfe简约梯度法(Reduced Gradient, RG)
3.4 广义简约梯度法(Generalized Reduced Gradient, GRG)
3.5 Frank-Wolfe方法
4. 惩罚函数法(Penalty Function Methods)
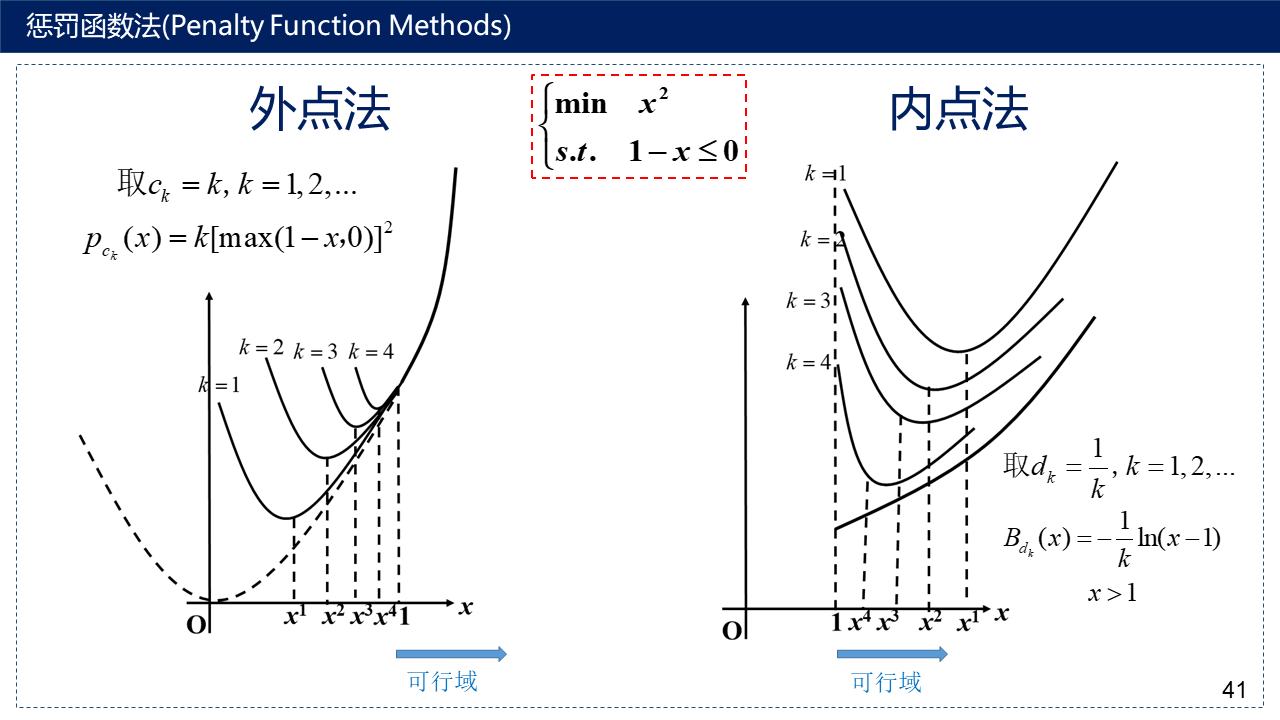
4.1 外点法/罚函数法(Exterior Penalty Function)
4.2 内点法/障碍函数法(Interior Penalty Function)
4.3 乘子法
5. 序列二次规划(Sequential Quadratic Programming)
5.1 Lagrange-Newton法
5.2 Wilson-Han-Powell法(也称SQP)
6. 参考文献
-
***在筠, 等, 运筹学(第三版), 高等教育出版社, 2007. (引言，外点法与内点法)
-
唐焕文, 等, 实用最优化方法, 大连理工大学社, 2004. http://www.wenqujingdian.com/Public/editor/attached/file/14/C0043739.pdf. (引言)
-
孙靖民, 等, 机械优化设计, 机械工业出版社, 2006. (直接搜索法)
-
陈宝林, 最优化理论与算法, 清华大学出版社, 2005. https://deitacloud.github.io/site/机器学习/. (可行方向法)
-
凯鲁嘎吉, 交替方向乘子法(Alternating Direction Method of Multipliers),博客园, https://www.cnblogs.com/kailugaji/p/12676095.html (乘子法)
-
高立, 数值最优化方法, 北京大学出版社, 2014. (序列二次规划)
