Deep Reinforcement Learning Hands-On——Policy Gradients – an Alternative
作者:凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/
更多请看:Reinforcement Learning - 随笔分类 - 凯鲁嘎吉 - 博客园 https://www.cnblogs.com/kailugaji/category/2038931.html
本文代码下载:https://github.com/kailugaji/Hands-on-Reinforcement-Learning/tree/main/03%20Policy%20Gradients
这一篇博文参考了书目《Deep Reinforcement Learning Hands-On Second Edition》第11章内容,主要介绍基于策略函数的强化学习方法,包括:REINFORCE、带基准线的REINFORCE算法(REINFORCE with Baseline)以及策略梯度方法(引入entropy bonus来增加探索,引入基准线来解决方差大训练不稳定问题)。具体理论知识,请参见:强化学习(Reinforcement Learning) - 凯鲁嘎吉 - 博客园。为了与DQN算法作对比,首先用Python重新实现了DQN算法(架构不是标准的三卷积两全连接,而是简化为两全连接) 01_cartpole_dqn.py,接着分别实现基于策略函数的三个强化学习方法02_cartpole_reinforce.py,03_cartpole_reinforce_baseline.py,与04_cartpole_pg.py,还有一个改进的策略梯度算法见:https://github.com/kailugaji/Hands-on-Reinforcement-Learning/blob/main/03%20Policy%20Gradients/05_pong_pg.py,该算法用到了梯度裁剪策略,多环境并行实现,采用移动平均法定义基准线,由于某些外在因素,结果并未列出,可自行运行。06_cartpole_pg.py是04_cartpole_pg.py的扩展,唯一的区别在于baseline可以由用户选择加或者不加,建议使用06_cartpole_pg.py。
值函数与策略函数方法的区别:基于值函数的方法网络输出的是Q值,而基于策略函数的方法网络输出的是动作的概率分布(代码里是输出Q值,再进行softmax得到概率分布),通过随机采样,得到最终的动作。
1. 01_cartpole_dqn.py
1.1 程序
#!/usr/bin/env python3
# -*- coding=utf-8 -*-
# DQN
# The CartPole example
# https://www.cnblogs.com/kailugaji/
import gym
import ptan
import numpy as np
from tensorboardX import SummaryWriter
import torch
import torch.nn as nn
import torch.optim as optim
GAMMA = 0.99 # 折扣率 0.9
LEARNING_RATE = 0.01 # 学习率 5e-3
BATCH_SIZE = 16 # 一批xx个样本 16
EPSILON_START = 1.0 # epsilon因子
EPSILON_STOP = 0.02
EPSILON_STEPS = 5000
REPLAY_BUFFER = 5000 # 经验回放池容量
# 构建网络
class DQN(nn.Module):
def __init__(self, input_size, n_actions):
# input_size:输入状态维度,hidden_size:隐层维度=128,n_actions:输出动作维度
super(DQN, self).__init__()
self.net = nn.Sequential(
nn.Linear(input_size, 128), # 全连接层,隐层预设为128维度
nn.ReLU(),
nn.Linear(128, n_actions) # 全连接层
)
def forward(self, x):
return self.net(x)
# 目标网络 r + gamma * max Q(s, a)
def calc_target(net, local_reward, next_state):
if next_state is None:
return local_reward
state_v = torch.tensor([next_state], dtype=torch.float32)
next_q_v = net(state_v) # 将最后的状态输入网络,得到Q(s, a)
best_q = next_q_v.max(dim=1)[0].item() # 找最大的Q
return local_reward + GAMMA * best_q
# r + gamma * max Q(s, a)
if __name__ == "__main__":
env = gym.make("CartPole-v0") # 创建游戏环境
writer = SummaryWriter(comment="-cartpole-dqn")
net = DQN(env.observation_space.shape[0], env.action_space.n) # 4(状态)->128->2(动作)
# print(net)
selector = ptan.actions.EpsilonGreedyActionSelector(epsilon=EPSILON_START)
# epsilon-greedy action selector,初始epsilon=1
agent = ptan.agent.DQNAgent(net, selector, preprocessor=ptan.agent.float32_preprocessor)
# DQNAgent:离散
# dqn_model换成自定义的DQN模型,4(状态)->128->2(动作)
exp_source = ptan.experience.ExperienceSourceFirstLast(env, agent, gamma=GAMMA)
# 返回运行记录以用于训练模型,输出格式为:(state, action, reward, last_state)
replay_buffer = ptan.experience.ExperienceReplayBuffer(exp_source, REPLAY_BUFFER)
# 经验回放池,构建buffer,容量为1000,当前没东西,len(buffer) = 0
optimizer = optim.Adam(net.parameters(), lr=LEARNING_RATE) # Adam优化
mse_loss = nn.MSELoss() # MSE loss
total_rewards = [] # the total rewards for the episodes
step_idx = 0 # 迭代次数/轮数
done_episodes = 0 # 局数,几局游戏
while True:
step_idx += 1
selector.epsilon = max(EPSILON_STOP, EPSILON_START - step_idx / EPSILON_STEPS)
# epsilon随迭代步数的衰减策略
replay_buffer.populate(1) # 从环境中获取一个新样本
if len(replay_buffer) < BATCH_SIZE: # buffer里面还没超过BATCH_SIZE个样本
continue
# sample batch
batch = replay_buffer.sample(BATCH_SIZE) # 从buffer里面均匀抽样一个批次的样本,一批BATCH_SIZE个样本
batch_states = [exp.state for exp in batch]
batch_actions = [exp.action for exp in batch]
batch_targets = [calc_target(net, exp.reward, exp.last_state)
for exp in batch] # r + gamma * max Q(s, a)
# train
optimizer.zero_grad()
states_v = torch.FloatTensor(batch_states)
net_q_v = net(states_v) # 输入状态,输出Q(s, a)值
target_q = net_q_v.data.numpy().copy() # copy网络参数
target_q[range(BATCH_SIZE), batch_actions] = batch_targets
target_q_v = torch.tensor(target_q) # r + gamma * max Q(s, a)
loss_v = mse_loss(net_q_v, target_q_v) # min L = (r + gamma * max Q(s', a') - Q(s, a))^2
loss_v.backward()
optimizer.step()
# handle new rewards
new_rewards = exp_source.pop_total_rewards() # 返回一局游戏过后的total_rewords
if new_rewards:
done_episodes += 1
reward = new_rewards[0]
total_rewards.append(reward) # 前done_episodes局游戏的奖励之和
mean_rewards = float(np.mean(total_rewards[-100:])) # total_rewards/done_episodes
print("第%d次: 第%d局游戏结束, 奖励为%6.2f, 平均奖励为%6.2f, epsilon为%.2f" % (step_idx, done_episodes, reward, mean_rewards, selector.epsilon))
writer.add_scalar("reward", reward, step_idx)
writer.add_scalar("reward_100", mean_rewards, step_idx)
writer.add_scalar("epsilon", selector.epsilon, step_idx)
writer.add_scalar("episodes", done_episodes, step_idx)
if mean_rewards > 50: # 最大期望奖励阈值,只有当平均奖励 > 50时才结束游戏
print("经过%d轮完成%d局游戏!" % (step_idx, done_episodes))
break
writer.close()
1.2 结果
第17次: 第1局游戏结束, 奖励为 16.00, 平均奖励为 16.00, epsilon为1.00
第40次: 第2局游戏结束, 奖励为 23.00, 平均奖励为 19.50, epsilon为0.99
第67次: 第3局游戏结束, 奖励为 27.00, 平均奖励为 22.00, epsilon为0.99
第105次: 第4局游戏结束, 奖励为 38.00, 平均奖励为 26.00, epsilon为0.98
第142次: 第5局游戏结束, 奖励为 37.00, 平均奖励为 28.20, epsilon为0.97
第161次: 第6局游戏结束, 奖励为 19.00, 平均奖励为 26.67, epsilon为0.97
第186次: 第7局游戏结束, 奖励为 25.00, 平均奖励为 26.43, epsilon为0.96
第197次: 第8局游戏结束, 奖励为 11.00, 平均奖励为 24.50, epsilon为0.96
第219次: 第9局游戏结束, 奖励为 22.00, 平均奖励为 24.22, epsilon为0.96
第249次: 第10局游戏结束, 奖励为 30.00, 平均奖励为 24.80, epsilon为0.95
第262次: 第11局游戏结束, 奖励为 13.00, 平均奖励为 23.73, epsilon为0.95
第283次: 第12局游戏结束, 奖励为 21.00, 平均奖励为 23.50, epsilon为0.94
第307次: 第13局游戏结束, 奖励为 24.00, 平均奖励为 23.54, epsilon为0.94
第333次: 第14局游戏结束, 奖励为 26.00, 平均奖励为 23.71, epsilon为0.93
第348次: 第15局游戏结束, 奖励为 15.00, 平均奖励为 23.13, epsilon为0.93
第387次: 第16局游戏结束, 奖励为 39.00, 平均奖励为 24.12, epsilon为0.92
第411次: 第17局游戏结束, 奖励为 24.00, 平均奖励为 24.12, epsilon为0.92
第429次: 第18局游戏结束, 奖励为 18.00, 平均奖励为 23.78, epsilon为0.91
第469次: 第19局游戏结束, 奖励为 40.00, 平均奖励为 24.63, epsilon为0.91
第481次: 第20局游戏结束, 奖励为 12.00, 平均奖励为 24.00, epsilon为0.90
第493次: 第21局游戏结束, 奖励为 12.00, 平均奖励为 23.43, epsilon为0.90
第513次: 第22局游戏结束, 奖励为 20.00, 平均奖励为 23.27, epsilon为0.90
第527次: 第23局游戏结束, 奖励为 14.00, 平均奖励为 22.87, epsilon为0.89
第578次: 第24局游戏结束, 奖励为 51.00, 平均奖励为 24.04, epsilon为0.88
第592次: 第25局游戏结束, 奖励为 14.00, 平均奖励为 23.64, epsilon为0.88
第604次: 第26局游戏结束, 奖励为 12.00, 平均奖励为 23.19, epsilon为0.88
第632次: 第27局游戏结束, 奖励为 28.00, 平均奖励为 23.37, epsilon为0.87
第664次: 第28局游戏结束, 奖励为 32.00, 平均奖励为 23.68, epsilon为0.87
第700次: 第29局游戏结束, 奖励为 36.00, 平均奖励为 24.10, epsilon为0.86
第711次: 第30局游戏结束, 奖励为 11.00, 平均奖励为 23.67, epsilon为0.86
第745次: 第31局游戏结束, 奖励为 34.00, 平均奖励为 24.00, epsilon为0.85
第760次: 第32局游戏结束, 奖励为 15.00, 平均奖励为 23.72, epsilon为0.85
第774次: 第33局游戏结束, 奖励为 14.00, 平均奖励为 23.42, epsilon为0.85
第798次: 第34局游戏结束, 奖励为 24.00, 平均奖励为 23.44, epsilon为0.84
第817次: 第35局游戏结束, 奖励为 19.00, 平均奖励为 23.31, epsilon为0.84
第829次: 第36局游戏结束, 奖励为 12.00, 平均奖励为 23.00, epsilon为0.83
第862次: 第37局游戏结束, 奖励为 33.00, 平均奖励为 23.27, epsilon为0.83
第881次: 第38局游戏结束, 奖励为 19.00, 平均奖励为 23.16, epsilon为0.82
第906次: 第39局游戏结束, 奖励为 25.00, 平均奖励为 23.21, epsilon为0.82
第929次: 第40局游戏结束, 奖励为 23.00, 平均奖励为 23.20, epsilon为0.81
第963次: 第41局游戏结束, 奖励为 34.00, 平均奖励为 23.46, epsilon为0.81
第987次: 第42局游戏结束, 奖励为 24.00, 平均奖励为 23.48, epsilon为0.80
第1017次: 第43局游戏结束, 奖励为 30.00, 平均奖励为 23.63, epsilon为0.80
第1062次: 第44局游戏结束, 奖励为 45.00, 平均奖励为 24.11, epsilon为0.79
第1131次: 第45局游戏结束, 奖励为 69.00, 平均奖励为 25.11, epsilon为0.77
第1163次: 第46局游戏结束, 奖励为 32.00, 平均奖励为 25.26, epsilon为0.77
第1173次: 第47局游戏结束, 奖励为 10.00, 平均奖励为 24.94, epsilon为0.77
第1190次: 第48局游戏结束, 奖励为 17.00, 平均奖励为 24.77, epsilon为0.76
第1222次: 第49局游戏结束, 奖励为 32.00, 平均奖励为 24.92, epsilon为0.76
第1243次: 第50局游戏结束, 奖励为 21.00, 平均奖励为 24.84, epsilon为0.75
第1265次: 第51局游戏结束, 奖励为 22.00, 平均奖励为 24.78, epsilon为0.75
第1277次: 第52局游戏结束, 奖励为 12.00, 平均奖励为 24.54, epsilon为0.74
第1292次: 第53局游戏结束, 奖励为 15.00, 平均奖励为 24.36, epsilon为0.74
第1325次: 第54局游戏结束, 奖励为 33.00, 平均奖励为 24.52, epsilon为0.73
第1341次: 第55局游戏结束, 奖励为 16.00, 平均奖励为 24.36, epsilon为0.73
第1370次: 第56局游戏结束, 奖励为 29.00, 平均奖励为 24.45, epsilon为0.73
第1403次: 第57局游戏结束, 奖励为 33.00, 平均奖励为 24.60, epsilon为0.72
第1422次: 第58局游戏结束, 奖励为 19.00, 平均奖励为 24.50, epsilon为0.72
第1471次: 第59局游戏结束, 奖励为 49.00, 平均奖励为 24.92, epsilon为0.71
第1483次: 第60局游戏结束, 奖励为 12.00, 平均奖励为 24.70, epsilon为0.70
第1594次: 第61局游戏结束, 奖励为111.00, 平均奖励为 26.11, epsilon为0.68
第1621次: 第62局游戏结束, 奖励为 27.00, 平均奖励为 26.13, epsilon为0.68
第1637次: 第63局游戏结束, 奖励为 16.00, 平均奖励为 25.97, epsilon为0.67
第1684次: 第64局游戏结束, 奖励为 47.00, 平均奖励为 26.30, epsilon为0.66
第1805次: 第65局游戏结束, 奖励为121.00, 平均奖励为 27.75, epsilon为0.64
第1855次: 第66局游戏结束, 奖励为 50.00, 平均奖励为 28.09, epsilon为0.63
第1904次: 第67局游戏结束, 奖励为 49.00, 平均奖励为 28.40, epsilon为0.62
第1924次: 第68局游戏结束, 奖励为 20.00, 平均奖励为 28.28, epsilon为0.62
第1967次: 第69局游戏结束, 奖励为 43.00, 平均奖励为 28.49, epsilon为0.61
第2042次: 第70局游戏结束, 奖励为 75.00, 平均奖励为 29.16, epsilon为0.59
第2075次: 第71局游戏结束, 奖励为 33.00, 平均奖励为 29.21, epsilon为0.58
第2110次: 第72局游戏结束, 奖励为 35.00, 平均奖励为 29.29, epsilon为0.58
第2127次: 第73局游戏结束, 奖励为 17.00, 平均奖励为 29.12, epsilon为0.57
第2161次: 第74局游戏结束, 奖励为 34.00, 平均奖励为 29.19, epsilon为0.57
第2219次: 第75局游戏结束, 奖励为 58.00, 平均奖励为 29.57, epsilon为0.56
第2238次: 第76局游戏结束, 奖励为 19.00, 平均奖励为 29.43, epsilon为0.55
第2300次: 第77局游戏结束, 奖励为 62.00, 平均奖励为 29.86, epsilon为0.54
第2348次: 第78局游戏结束, 奖励为 48.00, 平均奖励为 30.09, epsilon为0.53
第2454次: 第79局游戏结束, 奖励为106.00, 平均奖励为 31.05, epsilon为0.51
第2527次: 第80局游戏结束, 奖励为 73.00, 平均奖励为 31.57, epsilon为0.49
第2590次: 第81局游戏结束, 奖励为 63.00, 平均奖励为 31.96, epsilon为0.48
第2642次: 第82局游戏结束, 奖励为 52.00, 平均奖励为 32.21, epsilon为0.47
第2723次: 第83局游戏结束, 奖励为 81.00, 平均奖励为 32.80, epsilon为0.46
第2824次: 第84局游戏结束, 奖励为101.00, 平均奖励为 33.61, epsilon为0.44
第2865次: 第85局游戏结束, 奖励为 41.00, 平均奖励为 33.69, epsilon为0.43
第2957次: 第86局游戏结束, 奖励为 92.00, 平均奖励为 34.37, epsilon为0.41
第3067次: 第87局游戏结束, 奖励为110.00, 平均奖励为 35.24, epsilon为0.39
第3124次: 第88局游戏结束, 奖励为 57.00, 平均奖励为 35.49, epsilon为0.38
第3188次: 第89局游戏结束, 奖励为 64.00, 平均奖励为 35.81, epsilon为0.36
第3274次: 第90局游戏结束, 奖励为 86.00, 平均奖励为 36.37, epsilon为0.35
第3334次: 第91局游戏结束, 奖励为 60.00, 平均奖励为 36.63, epsilon为0.33
第3424次: 第92局游戏结束, 奖励为 90.00, 平均奖励为 37.21, epsilon为0.32
第3503次: 第93局游戏结束, 奖励为 79.00, 平均奖励为 37.66, epsilon为0.30
第3587次: 第94局游戏结束, 奖励为 84.00, 平均奖励为 38.15, epsilon为0.28
第3787次: 第95局游戏结束, 奖励为200.00, 平均奖励为 39.85, epsilon为0.24
第3879次: 第96局游戏结束, 奖励为 92.00, 平均奖励为 40.40, epsilon为0.22
第3965次: 第97局游戏结束, 奖励为 86.00, 平均奖励为 40.87, epsilon为0.21
第4070次: 第98局游戏结束, 奖励为105.00, 平均奖励为 41.52, epsilon为0.19
第4146次: 第99局游戏结束, 奖励为 76.00, 平均奖励为 41.87, epsilon为0.17
第4199次: 第100局游戏结束, 奖励为 53.00, 平均奖励为 41.98, epsilon为0.16
第4250次: 第101局游戏结束, 奖励为 51.00, 平均奖励为 42.33, epsilon为0.15
第4321次: 第102局游戏结束, 奖励为 71.00, 平均奖励为 42.81, epsilon为0.14
第4418次: 第103局游戏结束, 奖励为 97.00, 平均奖励为 43.51, epsilon为0.12
第4537次: 第104局游戏结束, 奖励为119.00, 平均奖励为 44.32, epsilon为0.09
第4680次: 第105局游戏结束, 奖励为143.00, 平均奖励为 45.38, epsilon为0.06
第4749次: 第106局游戏结束, 奖励为 69.00, 平均奖励为 45.88, epsilon为0.05
第4888次: 第107局游戏结束, 奖励为139.00, 平均奖励为 47.02, epsilon为0.02
第4941次: 第108局游戏结束, 奖励为 53.00, 平均奖励为 47.44, epsilon为0.02
第5106次: 第109局游戏结束, 奖励为165.00, 平均奖励为 48.87, epsilon为0.02
第5162次: 第110局游戏结束, 奖励为 56.00, 平均奖励为 49.13, epsilon为0.02
第5212次: 第111局游戏结束, 奖励为 50.00, 平均奖励为 49.50, epsilon为0.02
第5286次: 第112局游戏结束, 奖励为 74.00, 平均奖励为 50.03, epsilon为0.02
经过5286轮完成112局游戏!

epsilon衰减曲线
2. 02_cartpole_reinforce.py
2.1 程序
#!/usr/bin/env python3
# -*- coding=utf-8 -*-
# Policy Gradients——REINFORCE
# The CartPole example
# https://www.cnblogs.com/kailugaji/
import gym
import ptan
import numpy as np
from tensorboardX import SummaryWriter
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
GAMMA = 0.99 # 折扣率
LEARNING_RATE = 0.01 # 学习率
EPISODES_TO_TRAIN = 4 # how many complete episodes we will use for training
# 构建网络
class PGN(nn.Module):
def __init__(self, input_size, n_actions):
# input_size:输入状态维度,hidden_size:隐层维度=128,n_actions:输出动作维度
super(PGN, self).__init__()
self.net = nn.Sequential(
nn.Linear(input_size, 128), # 全连接层,隐层预设为128维度
nn.ReLU(),
nn.Linear(128, n_actions) # 全连接层
)
def forward(self, x):
return self.net(x) # 未用softmax
# Calculate the reward from the end of the local reward list.
# Indeed, the last step of the episode will have a total reward equal to its local reward.
# The step before the last will have the total reward of r(𝑡−1) + gamma * r(𝑡)
# sum(gamma^t * reward)
def calc_qvals(rewards):
res = []
sum_r = 0.0
for r in reversed(rewards): # reversed: 返回反向的迭代器对象
sum_r *= GAMMA # gamma * r(𝑡), r(t): the total reward for the previous steps
sum_r += r # r(𝑡−1) + gamma * r(𝑡), r(t-1): the local reward
res.append(sum_r) # the discounted total reward
return list(reversed(res)) # a list of rewards for the whole episode
if __name__ == "__main__":
env = gym.make("CartPole-v0") # 创建游戏环境
writer = SummaryWriter(comment="-cartpole-reinforce")
net = PGN(env.observation_space.shape[0], env.action_space.n) # 4(状态)->128->2(动作)
# print(net)
agent = ptan.agent.PolicyAgent(net, preprocessor=ptan.agent.float32_preprocessor, apply_softmax=True)
# PolicyAgent:连续
# make a decision about actions for every observation (依概率)
# apply_softmax=True:网络输出先经过softmax转化成概率,再从这个概率分布中进行随机抽样
# float32_preprocessor:returns the observation as float64 instead of the float32 required by PyTorch
exp_source = ptan.experience.ExperienceSourceFirstLast(env, agent, gamma=GAMMA)
# 返回运行记录以用于训练模型,输出格式为:(state, action, reward, last_state)
optimizer = optim.Adam(net.parameters(), lr=LEARNING_RATE) # Adam优化
total_rewards = [] # the total rewards for the episodes
step_idx = 0 # 迭代次数/轮数
done_episodes = 0 # 局数,几局游戏
batch_episodes = 0
batch_states, batch_actions, batch_qvals = [], [], []
cur_rewards = [] # local rewards for the episode being currently played
for step_idx, exp in enumerate(exp_source): # (state, action, reward, last_state)
batch_states.append(exp.state) # 状态
batch_actions.append(int(exp.action)) # 动作
cur_rewards.append(exp.reward) # 即时奖励
if exp.last_state is None: # 一局游戏结束
batch_qvals.extend(calc_qvals(cur_rewards)) # the discounted total rewards
cur_rewards.clear()
batch_episodes += 1
# handle new rewards
new_rewards = exp_source.pop_total_rewards() # 返回一局游戏过后的total_rewords
if new_rewards:
done_episodes += 1 # 游戏局数(回合数)
reward = new_rewards[0]
total_rewards.append(reward) # the total rewards for the episodes
mean_rewards = float(np.mean(total_rewards[-100:])) # 平均奖励
print("第%d次: 第%d局游戏结束, 奖励为%6.2f, 平均奖励为%6.2f" % (step_idx, done_episodes, reward, mean_rewards))
writer.add_scalar("reward", reward, step_idx)
writer.add_scalar("reward_100", mean_rewards, step_idx)
writer.add_scalar("episodes", done_episodes, step_idx)
if mean_rewards > 50: # 最大期望奖励阈值,只有当mean_rewards > 50时才结束游戏
print("经过%d轮完成%d局游戏!" % (step_idx, done_episodes))
break
if batch_episodes < EPISODES_TO_TRAIN: # how many complete episodes we will use for training
continue
# train
optimizer.zero_grad()
states_v = torch.FloatTensor(batch_states)
batch_actions_t = torch.LongTensor(batch_actions)
batch_qvals_v = torch.FloatTensor(batch_qvals) # the discounted batch total rewards
logits_v = net(states_v) # 输入状态,输出Q(s, a)值
log_prob_v = F.log_softmax(logits_v, dim=1) # 输出动作的对数概率分布 log π(s, a)
log_prob_actions_v = batch_qvals_v * log_prob_v[range(len(batch_states)), batch_actions_t]
# max sum(gamma^t * reward) * log π(s, a)
loss_v = -log_prob_actions_v.mean() # min
loss_v.backward()
optimizer.step()
batch_episodes = 0
batch_states.clear()
batch_actions.clear()
batch_qvals.clear()
writer.close()
2.2 结果
第21次: 第1局游戏结束, 奖励为 21.00, 平均奖励为 21.00
第65次: 第2局游戏结束, 奖励为 44.00, 平均奖励为 32.50
第78次: 第3局游戏结束, 奖励为 13.00, 平均奖励为 26.00
第91次: 第4局游戏结束, 奖励为 13.00, 平均奖励为 22.75
第112次: 第5局游戏结束, 奖励为 21.00, 平均奖励为 22.40
第131次: 第6局游戏结束, 奖励为 19.00, 平均奖励为 21.83
第158次: 第7局游戏结束, 奖励为 27.00, 平均奖励为 22.57
第173次: 第8局游戏结束, 奖励为 15.00, 平均奖励为 21.62
第199次: 第9局游戏结束, 奖励为 26.00, 平均奖励为 22.11
第212次: 第10局游戏结束, 奖励为 13.00, 平均奖励为 21.20
第240次: 第11局游戏结束, 奖励为 28.00, 平均奖励为 21.82
第267次: 第12局游戏结束, 奖励为 27.00, 平均奖励为 22.25
第289次: 第13局游戏结束, 奖励为 22.00, 平均奖励为 22.23
第310次: 第14局游戏结束, 奖励为 21.00, 平均奖励为 22.14
第335次: 第15局游戏结束, 奖励为 25.00, 平均奖励为 22.33
第377次: 第16局游戏结束, 奖励为 42.00, 平均奖励为 23.56
第386次: 第17局游戏结束, 奖励为 9.00, 平均奖励为 22.71
第442次: 第18局游戏结束, 奖励为 56.00, 平均奖励为 24.56
第463次: 第19局游戏结束, 奖励为 21.00, 平均奖励为 24.37
第510次: 第20局游戏结束, 奖励为 47.00, 平均奖励为 25.50
第572次: 第21局游戏结束, 奖励为 62.00, 平均奖励为 27.24
第627次: 第22局游戏结束, 奖励为 55.00, 平均奖励为 28.50
第671次: 第23局游戏结束, 奖励为 44.00, 平均奖励为 29.17
第761次: 第24局游戏结束, 奖励为 90.00, 平均奖励为 31.71
第797次: 第25局游戏结束, 奖励为 36.00, 平均奖励为 31.88
第873次: 第26局游戏结束, 奖励为 76.00, 平均奖励为 33.58
第932次: 第27局游戏结束, 奖励为 59.00, 平均奖励为 34.52
第965次: 第28局游戏结束, 奖励为 33.00, 平均奖励为 34.46
第1017次: 第29局游戏结束, 奖励为 52.00, 平均奖励为 35.07
第1047次: 第30局游戏结束, 奖励为 30.00, 平均奖励为 34.90
第1121次: 第31局游戏结束, 奖励为 74.00, 平均奖励为 36.16
第1139次: 第32局游戏结束, 奖励为 18.00, 平均奖励为 35.59
第1161次: 第33局游戏结束, 奖励为 22.00, 平均奖励为 35.18
第1329次: 第34局游戏结束, 奖励为168.00, 平均奖励为 39.09
第1361次: 第35局游戏结束, 奖励为 32.00, 平均奖励为 38.89
第1414次: 第36局游戏结束, 奖励为 53.00, 平均奖励为 39.28
第1431次: 第37局游戏结束, 奖励为 17.00, 平均奖励为 38.68
第1519次: 第38局游戏结束, 奖励为 88.00, 平均奖励为 39.97
第1552次: 第39局游戏结束, 奖励为 33.00, 平均奖励为 39.79
第1568次: 第40局游戏结束, 奖励为 16.00, 平均奖励为 39.20
第1614次: 第41局游戏结束, 奖励为 46.00, 平均奖励为 39.37
第1674次: 第42局游戏结束, 奖励为 60.00, 平均奖励为 39.86
第1750次: 第43局游戏结束, 奖励为 76.00, 平均奖励为 40.70
第1802次: 第44局游戏结束, 奖励为 52.00, 平均奖励为 40.95
第1854次: 第45局游戏结束, 奖励为 52.00, 平均奖励为 41.20
第1897次: 第46局游戏结束, 奖励为 43.00, 平均奖励为 41.24
第1994次: 第47局游戏结束, 奖励为 97.00, 平均奖励为 42.43
第2051次: 第48局游戏结束, 奖励为 57.00, 平均奖励为 42.73
第2105次: 第49局游戏结束, 奖励为 54.00, 平均奖励为 42.96
第2169次: 第50局游戏结束, 奖励为 64.00, 平均奖励为 43.38
第2202次: 第51局游戏结束, 奖励为 33.00, 平均奖励为 43.18
第2220次: 第52局游戏结束, 奖励为 18.00, 平均奖励为 42.69
第2254次: 第53局游戏结束, 奖励为 34.00, 平均奖励为 42.53
第2310次: 第54局游戏结束, 奖励为 56.00, 平均奖励为 42.78
第2367次: 第55局游戏结束, 奖励为 57.00, 平均奖励为 43.04
第2450次: 第56局游戏结束, 奖励为 83.00, 平均奖励为 43.75
第2496次: 第57局游戏结束, 奖励为 46.00, 平均奖励为 43.79
第2532次: 第58局游戏结束, 奖励为 36.00, 平均奖励为 43.66
第2554次: 第59局游戏结束, 奖励为 22.00, 平均奖励为 43.29
第2599次: 第60局游戏结束, 奖励为 45.00, 平均奖励为 43.32
第2630次: 第61局游戏结束, 奖励为 31.00, 平均奖励为 43.11
第2659次: 第62局游戏结束, 奖励为 29.00, 平均奖励为 42.89
第2708次: 第63局游戏结束, 奖励为 49.00, 平均奖励为 42.98
第2772次: 第64局游戏结束, 奖励为 64.00, 平均奖励为 43.31
第2801次: 第65局游戏结束, 奖励为 29.00, 平均奖励为 43.09
第2830次: 第66局游戏结束, 奖励为 29.00, 平均奖励为 42.88
第2878次: 第67局游戏结束, 奖励为 48.00, 平均奖励为 42.96
第2928次: 第68局游戏结束, 奖励为 50.00, 平均奖励为 43.06
第2947次: 第69局游戏结束, 奖励为 19.00, 平均奖励为 42.71
第2973次: 第70局游戏结束, 奖励为 26.00, 平均奖励为 42.47
第3004次: 第71局游戏结束, 奖励为 31.00, 平均奖励为 42.31
第3050次: 第72局游戏结束, 奖励为 46.00, 平均奖励为 42.36
第3073次: 第73局游戏结束, 奖励为 23.00, 平均奖励为 42.10
第3149次: 第74局游戏结束, 奖励为 76.00, 平均奖励为 42.55
第3193次: 第75局游戏结束, 奖励为 44.00, 平均奖励为 42.57
第3216次: 第76局游戏结束, 奖励为 23.00, 平均奖励为 42.32
第3272次: 第77局游戏结束, 奖励为 56.00, 平均奖励为 42.49
第3327次: 第78局游戏结束, 奖励为 55.00, 平均奖励为 42.65
第3401次: 第79局游戏结束, 奖励为 74.00, 平均奖励为 43.05
第3457次: 第80局游戏结束, 奖励为 56.00, 平均奖励为 43.21
第3486次: 第81局游戏结束, 奖励为 29.00, 平均奖励为 43.04
第3531次: 第82局游戏结束, 奖励为 45.00, 平均奖励为 43.06
第3583次: 第83局游戏结束, 奖励为 52.00, 平均奖励为 43.17
第3600次: 第84局游戏结束, 奖励为 17.00, 平均奖励为 42.86
第3661次: 第85局游戏结束, 奖励为 61.00, 平均奖励为 43.07
第3688次: 第86局游戏结束, 奖励为 27.00, 平均奖励为 42.88
第3751次: 第87局游戏结束, 奖励为 63.00, 平均奖励为 43.11
第3825次: 第88局游戏结束, 奖励为 74.00, 平均奖励为 43.47
第3973次: 第89局游戏结束, 奖励为148.00, 平均奖励为 44.64
第4033次: 第90局游戏结束, 奖励为 60.00, 平均奖励为 44.81
第4103次: 第91局游戏结束, 奖励为 70.00, 平均奖励为 45.09
第4160次: 第92局游戏结束, 奖励为 57.00, 平均奖励为 45.22
第4192次: 第93局游戏结束, 奖励为 32.00, 平均奖励为 45.08
第4255次: 第94局游戏结束, 奖励为 63.00, 平均奖励为 45.27
第4326次: 第95局游戏结束, 奖励为 71.00, 平均奖励为 45.54
第4397次: 第96局游戏结束, 奖励为 71.00, 平均奖励为 45.80
第4453次: 第97局游戏结束, 奖励为 56.00, 平均奖励为 45.91
第4483次: 第98局游戏结束, 奖励为 30.00, 平均奖励为 45.74
第4521次: 第99局游戏结束, 奖励为 38.00, 平均奖励为 45.67
第4608次: 第100局游戏结束, 奖励为 87.00, 平均奖励为 46.08
第4690次: 第101局游戏结束, 奖励为 82.00, 平均奖励为 46.69
第4737次: 第102局游戏结束, 奖励为 47.00, 平均奖励为 46.72
第4801次: 第103局游戏结束, 奖励为 64.00, 平均奖励为 47.23
第4893次: 第104局游戏结束, 奖励为 92.00, 平均奖励为 48.02
第4981次: 第105局游戏结束, 奖励为 88.00, 平均奖励为 48.69
第5038次: 第106局游戏结束, 奖励为 57.00, 平均奖励为 49.07
第5109次: 第107局游戏结束, 奖励为 71.00, 平均奖励为 49.51
第5138次: 第108局游戏结束, 奖励为 29.00, 平均奖励为 49.65
第5189次: 第109局游戏结束, 奖励为 51.00, 平均奖励为 49.90
第5278次: 第110局游戏结束, 奖励为 89.00, 平均奖励为 50.66
经过5278轮完成110局游戏!
3. 03_cartpole_reinforce_baseline.py
3.1 程序
#!/usr/bin/env python3
# -*- coding=utf-8 -*-
# Policy Gradients——带基准线的REINFORCE算法(REINFORCE with Baseline)
# REINFORCE算法缺点:不同路径之间的方差大,导致训练不稳定
# 引入一控制变量sum(gamma^t * reward)的期望:E(sum(gamma^t * reward)),以减小方差
# Baseline:the mean of the discounted rewards
# The CartPole example
# https://www.cnblogs.com/kailugaji/
import gym
import ptan
import numpy as np
from tensorboardX import SummaryWriter
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
GAMMA = 0.99 # 折扣率
LEARNING_RATE = 0.01 # 学习率
EPISODES_TO_TRAIN = 4 # how many complete episodes we will use for training
# 构建网络
class PGN(nn.Module):
def __init__(self, input_size, n_actions):
# input_size:输入状态维度,hidden_size:隐层维度=128,n_actions:输出动作维度
super(PGN, self).__init__()
self.net = nn.Sequential(
nn.Linear(input_size, 128), # 全连接层,隐层预设为128维度
nn.ReLU(),
nn.Linear(128, n_actions) # 全连接层
)
def forward(self, x):
return self.net(x) # 未用softmax
# 与上一个程序唯一的不同在这!!!
# sum(gamma^t * reward) - E(sum(gamma^t * reward))
def calc_qvals(rewards):
res = []
sum_r = 0.0
for r in reversed(rewards):
sum_r *= GAMMA
sum_r += r
res.append(sum_r)
res = list(reversed(res))
mean_q = np.mean(res)
return [q - mean_q for q in res]
if __name__ == "__main__":
env = gym.make("CartPole-v0") # 创建游戏环境
writer = SummaryWriter(comment="-cartpole-reinforce-baseline")
net = PGN(env.observation_space.shape[0], env.action_space.n) # 4(状态)->128->2(动作)
# print(net)
agent = ptan.agent.PolicyAgent(net, preprocessor=ptan.agent.float32_preprocessor,apply_softmax=True)
# PolicyAgent:连续
# make a decision about actions for every observation (依概率)
# apply_softmax=True:网络输出先经过softmax转化成概率,再从这个概率分布中进行随机抽样
# float32_preprocessor:returns the observation as float64 instead of the float32 required by PyTorch
exp_source = ptan.experience.ExperienceSourceFirstLast(env, agent, gamma=GAMMA)
# 返回运行记录以用于训练模型,输出格式为:(state, action, reward, last_state)
optimizer = optim.Adam(net.parameters(), lr=LEARNING_RATE) # Adam优化
total_rewards = [] # 前几局的奖励之和
step_idx = 0 # 迭代次数/轮数
done_episodes = 0 # 局数,几局游戏
batch_episodes = 0
batch_states, batch_actions, batch_qvals = [], [], []
cur_states, cur_actions, cur_rewards = [], [], []
for step_idx, exp in enumerate(exp_source): # (state, action, reward, last_state)
cur_states.append(exp.state) # 状态
cur_actions.append(int(exp.action)) # 动作
cur_rewards.append(exp.reward) # 即时奖励
if exp.last_state is None: # 一局游戏结束
batch_states.extend(cur_states)
batch_actions.extend(cur_actions)
batch_qvals.extend(calc_qvals(cur_rewards))
cur_states.clear()
cur_actions.clear()
cur_rewards.clear()
batch_episodes += 1
# handle new rewards
new_rewards = exp_source.pop_total_rewards() # 返回一局游戏过后的total_rewords
if new_rewards:
done_episodes += 1 # 游戏局数(回合数)
reward = new_rewards[0]
total_rewards.append(reward) # the total rewards for the episodes
mean_rewards = float(np.mean(total_rewards[-100:])) # 平均奖励
print("第%d次: 第%d局游戏结束, 奖励为%6.2f, 平均奖励为%6.2f" % (step_idx, done_episodes, reward, mean_rewards))
writer.add_scalar("reward", reward, step_idx)
writer.add_scalar("reward_100", mean_rewards, step_idx)
writer.add_scalar("episodes", done_episodes, step_idx)
if mean_rewards > 50: # 最大期望奖励阈值,只有当mean_rewards > 50时才结束游戏
print("经过%d轮完成%d局游戏!" % (step_idx, done_episodes))
break
if batch_episodes < EPISODES_TO_TRAIN: # how many complete episodes we will use for training
continue
states_v = torch.FloatTensor(batch_states)
batch_actions_t = torch.LongTensor(batch_actions)
batch_qvals_v = torch.FloatTensor(batch_qvals)
# train
optimizer.zero_grad()
logits_v = net(states_v) # 输入状态,输出Q(s, a)值
log_prob_v = F.log_softmax(logits_v, dim=1) # 输出动作的对数概率分布 log π(s, a)
log_prob_actions_v = batch_qvals_v * log_prob_v[range(len(batch_states)), batch_actions_t]
# max (sum(gamma^t * reward) - E(sum(gamma^t * reward))) * log π(s, a)
loss_v = -log_prob_actions_v.mean() # min
loss_v.backward()
optimizer.step()
batch_episodes = 0
batch_states.clear()
batch_actions.clear()
batch_qvals.clear()
writer.close()
3.2 结果
第14次: 第1局游戏结束, 奖励为 14.00, 平均奖励为 14.00
第35次: 第2局游戏结束, 奖励为 21.00, 平均奖励为 17.50
第63次: 第3局游戏结束, 奖励为 28.00, 平均奖励为 21.00
第84次: 第4局游戏结束, 奖励为 21.00, 平均奖励为 21.00
第115次: 第5局游戏结束, 奖励为 31.00, 平均奖励为 23.00
第131次: 第6局游戏结束, 奖励为 16.00, 平均奖励为 21.83
第146次: 第7局游戏结束, 奖励为 15.00, 平均奖励为 20.86
第180次: 第8局游戏结束, 奖励为 34.00, 平均奖励为 22.50
第222次: 第9局游戏结束, 奖励为 42.00, 平均奖励为 24.67
第260次: 第10局游戏结束, 奖励为 38.00, 平均奖励为 26.00
第273次: 第11局游戏结束, 奖励为 13.00, 平均奖励为 24.82
第300次: 第12局游戏结束, 奖励为 27.00, 平均奖励为 25.00
第324次: 第13局游戏结束, 奖励为 24.00, 平均奖励为 24.92
第346次: 第14局游戏结束, 奖励为 22.00, 平均奖励为 24.71
第376次: 第15局游戏结束, 奖励为 30.00, 平均奖励为 25.07
第445次: 第16局游戏结束, 奖励为 69.00, 平均奖励为 27.81
第520次: 第17局游戏结束, 奖励为 75.00, 平均奖励为 30.59
第603次: 第18局游戏结束, 奖励为 83.00, 平均奖励为 33.50
第640次: 第19局游戏结束, 奖励为 37.00, 平均奖励为 33.68
第715次: 第20局游戏结束, 奖励为 75.00, 平均奖励为 35.75
第775次: 第21局游戏结束, 奖励为 60.00, 平均奖励为 36.90
第798次: 第22局游戏结束, 奖励为 23.00, 平均奖励为 36.27
第822次: 第23局游戏结束, 奖励为 24.00, 平均奖励为 35.74
第840次: 第24局游戏结束, 奖励为 18.00, 平均奖励为 35.00
第872次: 第25局游戏结束, 奖励为 32.00, 平均奖励为 34.88
第922次: 第26局游戏结束, 奖励为 50.00, 平均奖励为 35.46
第1016次: 第27局游戏结束, 奖励为 94.00, 平均奖励为 37.63
第1037次: 第28局游戏结束, 奖励为 21.00, 平均奖励为 37.04
第1083次: 第29局游戏结束, 奖励为 46.00, 平均奖励为 37.34
第1107次: 第30局游戏结束, 奖励为 24.00, 平均奖励为 36.90
第1153次: 第31局游戏结束, 奖励为 46.00, 平均奖励为 37.19
第1212次: 第32局游戏结束, 奖励为 59.00, 平均奖励为 37.88
第1245次: 第33局游戏结束, 奖励为 33.00, 平均奖励为 37.73
第1280次: 第34局游戏结束, 奖励为 35.00, 平均奖励为 37.65
第1359次: 第35局游戏结束, 奖励为 79.00, 平均奖励为 38.83
第1391次: 第36局游戏结束, 奖励为 32.00, 平均奖励为 38.64
第1524次: 第37局游戏结束, 奖励为133.00, 平均奖励为 41.19
第1581次: 第38局游戏结束, 奖励为 57.00, 平均奖励为 41.61
第1764次: 第39局游戏结束, 奖励为183.00, 平均奖励为 45.23
第1847次: 第40局游戏结束, 奖励为 83.00, 平均奖励为 46.17
第1898次: 第41局游戏结束, 奖励为 51.00, 平均奖励为 46.29
第1973次: 第42局游戏结束, 奖励为 75.00, 平均奖励为 46.98
第1996次: 第43局游戏结束, 奖励为 23.00, 平均奖励为 46.42
第2022次: 第44局游戏结束, 奖励为 26.00, 平均奖励为 45.95
第2092次: 第45局游戏结束, 奖励为 70.00, 平均奖励为 46.49
第2120次: 第46局游戏结束, 奖励为 28.00, 平均奖励为 46.09
第2154次: 第47局游戏结束, 奖励为 34.00, 平均奖励为 45.83
第2257次: 第48局游戏结束, 奖励为103.00, 平均奖励为 47.02
第2334次: 第49局游戏结束, 奖励为 77.00, 平均奖励为 47.63
第2439次: 第50局游戏结束, 奖励为105.00, 平均奖励为 48.78
第2508次: 第51局游戏结束, 奖励为 69.00, 平均奖励为 49.18
第2543次: 第52局游戏结束, 奖励为 35.00, 平均奖励为 48.90
第2630次: 第53局游戏结束, 奖励为 87.00, 平均奖励为 49.62
第2685次: 第54局游戏结束, 奖励为 55.00, 平均奖励为 49.72
第2705次: 第55局游戏结束, 奖励为 20.00, 平均奖励为 49.18
第2752次: 第56局游戏结束, 奖励为 47.00, 平均奖励为 49.14
第2862次: 第57局游戏结束, 奖励为110.00, 平均奖励为 50.21
经过2862轮完成57局游戏!
4. 04_cartpole_pg.py
4.1 程序
#!/usr/bin/env python3
# -*- coding=utf-8 -*-
# Policy gradient methods on CartPole
# 为增加探索,引入entropy bonus(信息熵正则项)
# 为了鼓励模型加入更多的不确定性,这样在训练的时候,模型就会去探索更多的可能性
# H(π) = - sum(π(a|s) * log π(a|s))
# min -(the discounted reward - baseline) * log π(s, a) + beta * sum (π(s, a) * log π(s, a))
# https://www.cnblogs.com/kailugaji/
import gym
import ptan
import numpy as np
from tensorboardX import SummaryWriter
from typing import Optional
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
GAMMA = 0.99 # 折扣率
LEARNING_RATE = 0.01 # 学习率
ENTROPY_BETA = 0.01 # 熵正则化因子 the scale of the entropy bonus
BATCH_SIZE = 16 # 一批xx个样本
REWARD_STEPS = 10
# 用于说明一条记录中包含的步(step)数 (sub-trajectories of length 10)
# how many steps ahead the Bellman equation is unrolled to estimate the discounted total reward of every transition.
# 构建网络
class PGN(nn.Module):
def __init__(self, input_size, n_actions):
# input_size:输入状态维度,hidden_size:隐层维度=128,n_actions:输出动作维度
super(PGN, self).__init__()
self.net = nn.Sequential(
nn.Linear(input_size, 128), # 全连接层,隐层预设为128维度
nn.ReLU(),
nn.Linear(128, n_actions) # 全连接层
)
def forward(self, x):
return self.net(x) # 未用softmax
# 平滑
def smooth(old: Optional[float], val: float, alpha: float = 0.95) -> float:
if old is None:
return val
return old * alpha + (1-alpha)*val
if __name__ == "__main__":
env = gym.make("CartPole-v0") # 创建游戏环境
writer = SummaryWriter(comment="-cartpole-pg")
net = PGN(env.observation_space.shape[0], env.action_space.n) # 4(状态)->128->2(动作)
# print(net)
agent = ptan.agent.PolicyAgent(net, preprocessor=ptan.agent.float32_preprocessor, apply_softmax=True)
# PolicyAgent:连续
# make a decision about actions for every observation (依概率)
# apply_softmax=True:网络输出先经过softmax转化成概率,再从这个概率分布中进行随机抽样
# float32_preprocessor:returns the observation as float64 instead of the float32 required by PyTorch
exp_source = ptan.experience.ExperienceSourceFirstLast(env, agent, gamma=GAMMA, steps_count=REWARD_STEPS)
# 返回运行记录以用于训练模型,输出格式为:(state, action, reward, last_state)
# 并不会输出每一步的信息,而是把多步的交互结果综合(累计多步的reward;显示头尾的状态)到一条Experience输出
# 多步rewards的累加是有衰退的,而其中的衰退系数由参数gamma(折扣率)指定,即reward=r1+gamma∗r2+(gamma^2)∗r3
# 其中rn代表第n步操作获得的reward
# last_state: the state we've got after executing the action. If our episode ends, we have None here
# steps_count=REWARD_STEPS:unroll the Bellman equation for 10 steps
optimizer = optim.Adam(net.parameters(), lr=LEARNING_RATE) # Adam优化
total_rewards = [] # 前几局的奖励之和
step_rewards = []
step_idx = 0 # 迭代次数/轮数
done_episodes = 0 # 局数,几局游戏
reward_sum = 0.0 # the sum of the discounted reward for every transition
bs_smoothed = entropy = l_entropy = l_policy = l_total = None
batch_states, batch_actions, batch_scales = [], [], []
for step_idx, exp in enumerate(exp_source): # (state, action, reward, last_state)
reward_sum += exp.reward # the sum of the discounted reward for every transition
baseline = reward_sum / (step_idx + 1) # 奖励除以迭代次数(步数) the baseline for the policy scale
writer.add_scalar("baseline", baseline, step_idx)
batch_states.append(exp.state) # 状态
batch_actions.append(int(exp.action)) # 动作
batch_scales.append(exp.reward - baseline) # 优势函数,引入基准
# handle new rewards
new_rewards = exp_source.pop_total_rewards() # 返回一局游戏过后的total_rewords
if new_rewards:
done_episodes += 1 # 游戏局数(回合数)
reward = new_rewards[0] # 本局游戏奖励
total_rewards.append(reward) # 前几局的奖励之和
mean_rewards = float(np.mean(total_rewards[-100:])) # 前几局的奖励之和/回合数
print("第%d次: 第%d局游戏结束, 奖励为%6.2f, 平均奖励为%6.2f" % (step_idx, done_episodes, reward, mean_rewards))
writer.add_scalar("reward", reward, step_idx) # 本局游戏奖励
writer.add_scalar("reward_100", mean_rewards, step_idx) # 前几局游戏的平均奖励
writer.add_scalar("episodes", done_episodes, step_idx) # 游戏局数(回合数)
if mean_rewards > 50: # 最大期望奖励阈值,只有当mean_rewards > 50时才结束游戏
print("经过%d轮完成%d局游戏!" % (step_idx, done_episodes))
break
if len(batch_states) < BATCH_SIZE: # state里面还没超过BATCH_SIZE个样本
continue
states_v = torch.FloatTensor(batch_states)
batch_actions_t = torch.LongTensor(batch_actions)
batch_scale_v = torch.FloatTensor(batch_scales) # 优势函数,引入基准
# train
optimizer.zero_grad()
logits_v = net(states_v) # 输入状态,输出Q(s, a)值
log_prob_v = F.log_softmax(logits_v, dim=1) # 输出动作的对数概率分布 log π(s, a)
log_prob_actions_v = batch_scale_v * log_prob_v[range(BATCH_SIZE), batch_actions_t]
# max (the discounted reward - baseline) * log π(s, a)
loss_policy_v = -log_prob_actions_v.mean() # min
# add the entropy bonus to the loss
prob_v = F.softmax(logits_v, dim=1) # 输出动作的概率分布π(s, a)
entropy_v = -(prob_v * log_prob_v).sum(dim=1).mean() # 熵正则项
# 信息熵的计算公式:entropy = -sum (π(s, a) * log π(s, a))
entropy_loss_v = -ENTROPY_BETA * entropy_v # loss = - beta * entropy
loss_v = loss_policy_v + entropy_loss_v
# min -(the discounted reward - baseline) * log π(s, a) + beta * sum (π(s, a) * log π(s, a))
loss_v.backward()
optimizer.step()
# calculate the Kullback-Leibler (KL) divergence between the new policy and the old policy
new_logits_v = net(states_v) # 输入状态,输出Q(s, a)值
new_prob_v = F.softmax(new_logits_v, dim=1) # 输出动作的概率分布π(s, a)
kl_div_v = -((new_prob_v / prob_v).log() * prob_v).sum(dim=1).mean()
# KL散度的计算公式:KL = - sum(log(π'(s, a)/π(s, a)) * π(s, a))
writer.add_scalar("kl", kl_div_v.item(), step_idx)
# calculate the statistics about the gradients on this training step
grad_max = 0.0
grad_means = 0.0
grad_count = 0
for p in net.parameters():
grad_max = max(grad_max, p.grad.abs().max().item()) # the graph of the maximum
grad_means += (p.grad ** 2).mean().sqrt().item() # L2 norm of gradients
grad_count += 1
# 下面实际上没有平滑,返回实际值(这5行代码在本程序中没意义)
bs_smoothed = smooth(bs_smoothed, np.mean(batch_scales))
entropy = smooth(entropy, entropy_v.item())
l_entropy = smooth(l_entropy, entropy_loss_v.item())
l_policy = smooth(l_policy, loss_policy_v.item())
l_total = smooth(l_total, loss_v.item())
writer.add_scalar("baseline", baseline, step_idx)
writer.add_scalar("entropy", entropy, step_idx)
writer.add_scalar("loss_entropy", l_entropy, step_idx)
writer.add_scalar("loss_policy", l_policy, step_idx)
writer.add_scalar("loss_total", l_total, step_idx)
writer.add_scalar("grad_l2", grad_means / grad_count, step_idx)
writer.add_scalar("grad_max", grad_max, step_idx)
writer.add_scalar("batch_scales", bs_smoothed, step_idx)
batch_states.clear()
batch_actions.clear()
batch_scales.clear()
writer.close()
4.2 结果
第16次: 第1局游戏结束, 奖励为 16.00, 平均奖励为 16.00
第35次: 第2局游戏结束, 奖励为 19.00, 平均奖励为 17.50
第72次: 第3局游戏结束, 奖励为 37.00, 平均奖励为 24.00
第90次: 第4局游戏结束, 奖励为 18.00, 平均奖励为 22.50
第100次: 第5局游戏结束, 奖励为 10.00, 平均奖励为 20.00
第121次: 第6局游戏结束, 奖励为 21.00, 平均奖励为 20.17
第130次: 第7局游戏结束, 奖励为 9.00, 平均奖励为 18.57
第143次: 第8局游戏结束, 奖励为 13.00, 平均奖励为 17.88
第156次: 第9局游戏结束, 奖励为 13.00, 平均奖励为 17.33
第170次: 第10局游戏结束, 奖励为 14.00, 平均奖励为 17.00
第185次: 第11局游戏结束, 奖励为 15.00, 平均奖励为 16.82
第198次: 第12局游戏结束, 奖励为 13.00, 平均奖励为 16.50
第224次: 第13局游戏结束, 奖励为 26.00, 平均奖励为 17.23
第253次: 第14局游戏结束, 奖励为 29.00, 平均奖励为 18.07
第323次: 第15局游戏结束, 奖励为 70.00, 平均奖励为 21.53
第356次: 第16局游戏结束, 奖励为 33.00, 平均奖励为 22.25
第388次: 第17局游戏结束, 奖励为 32.00, 平均奖励为 22.82
第414次: 第18局游戏结束, 奖励为 26.00, 平均奖励为 23.00
第442次: 第19局游戏结束, 奖励为 28.00, 平均奖励为 23.26
第536次: 第20局游戏结束, 奖励为 94.00, 平均奖励为 26.80
第589次: 第21局游戏结束, 奖励为 53.00, 平均奖励为 28.05
第652次: 第22局游戏结束, 奖励为 63.00, 平均奖励为 29.64
第753次: 第23局游戏结束, 奖励为101.00, 平均奖励为 32.74
第860次: 第24局游戏结束, 奖励为107.00, 平均奖励为 35.83
第904次: 第25局游戏结束, 奖励为 44.00, 平均奖励为 36.16
第984次: 第26局游戏结束, 奖励为 80.00, 平均奖励为 37.85
第1174次: 第27局游戏结束, 奖励为190.00, 平均奖励为 43.48
第1236次: 第28局游戏结束, 奖励为 62.00, 平均奖励为 44.14
第1317次: 第29局游戏结束, 奖励为 81.00, 平均奖励为 45.41
第1381次: 第30局游戏结束, 奖励为 64.00, 平均奖励为 46.03
第1581次: 第31局游戏结束, 奖励为200.00, 平均奖励为 51.00
经过1581轮完成31局游戏!
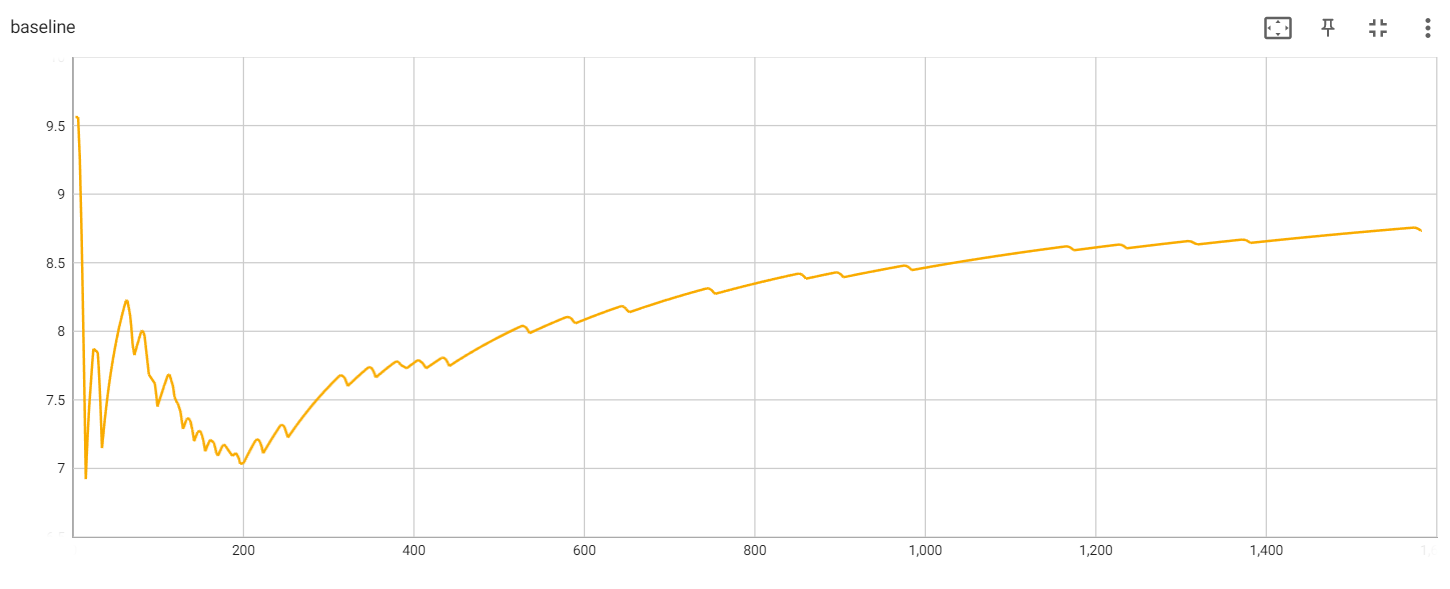
The baseline value during the training
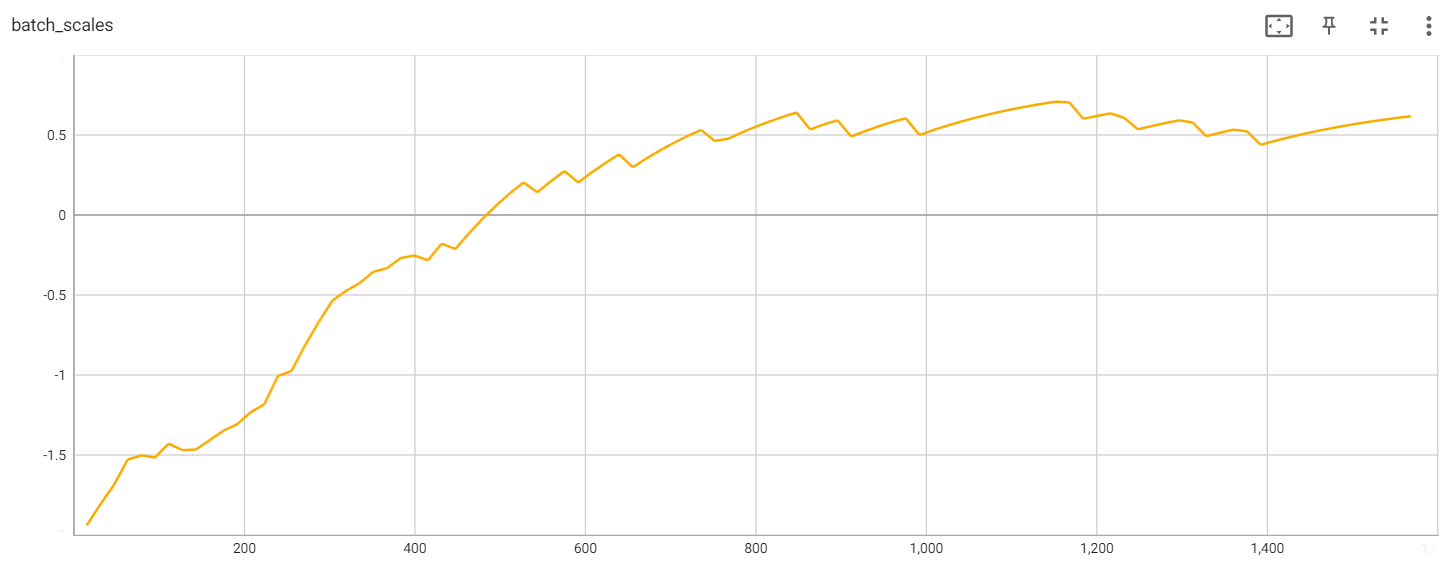
Batch scales
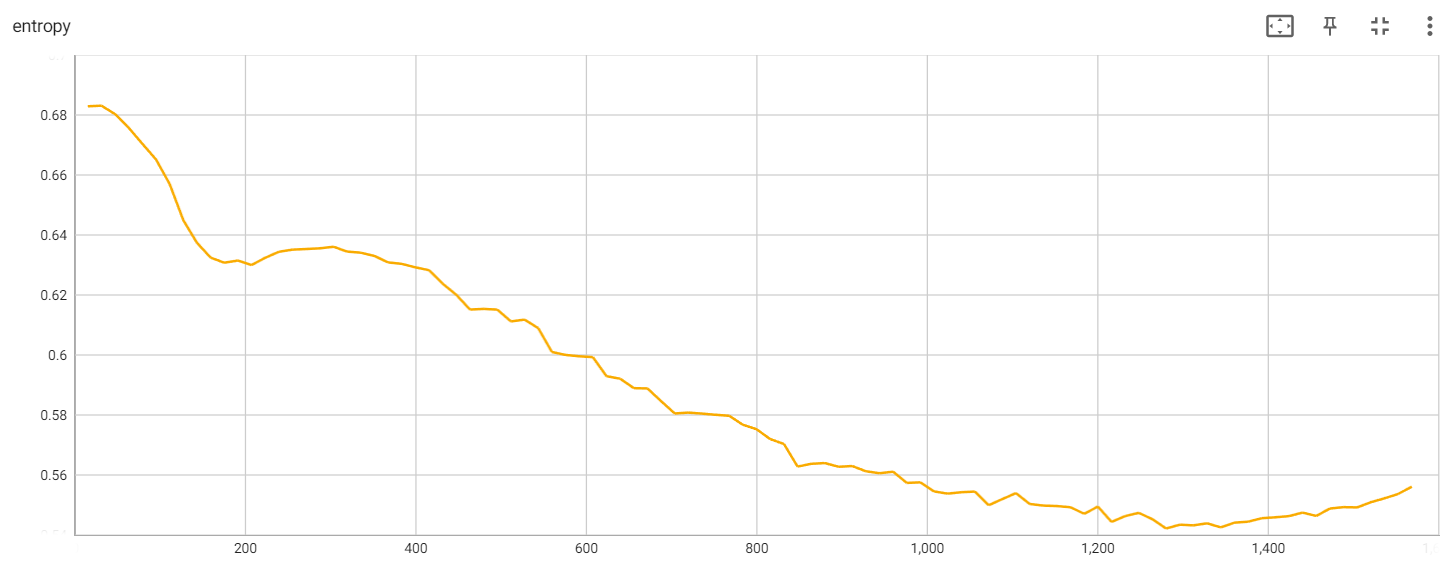
Entropy during the training
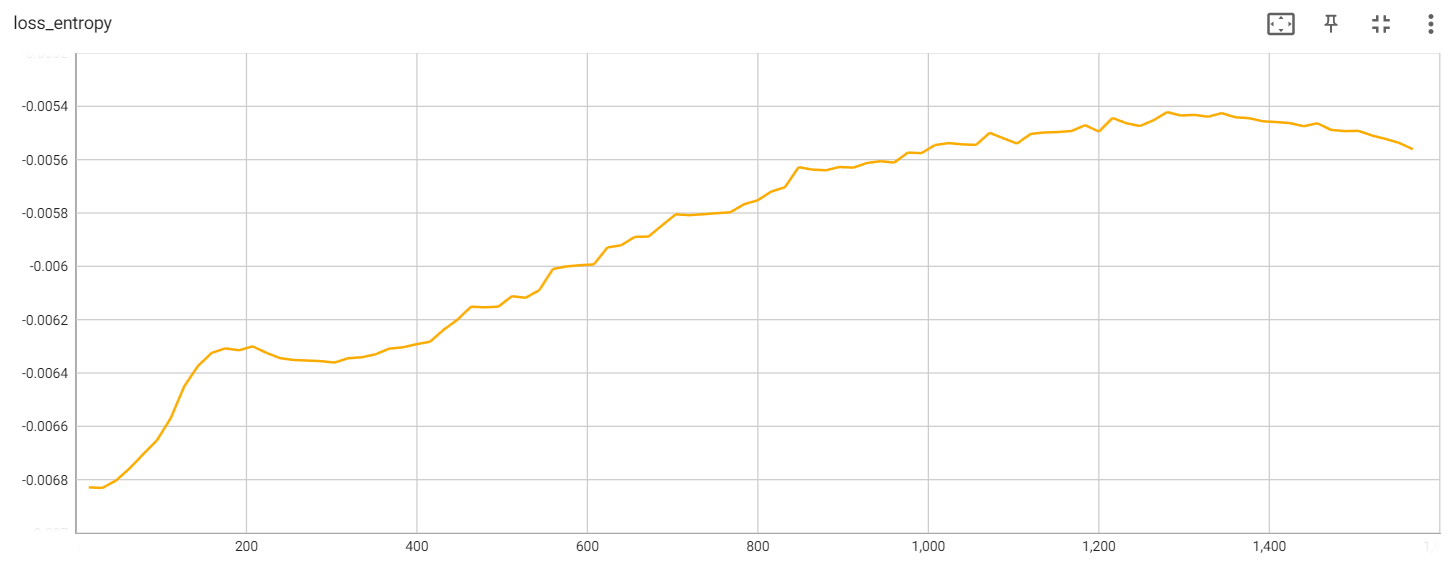
Entropy loss
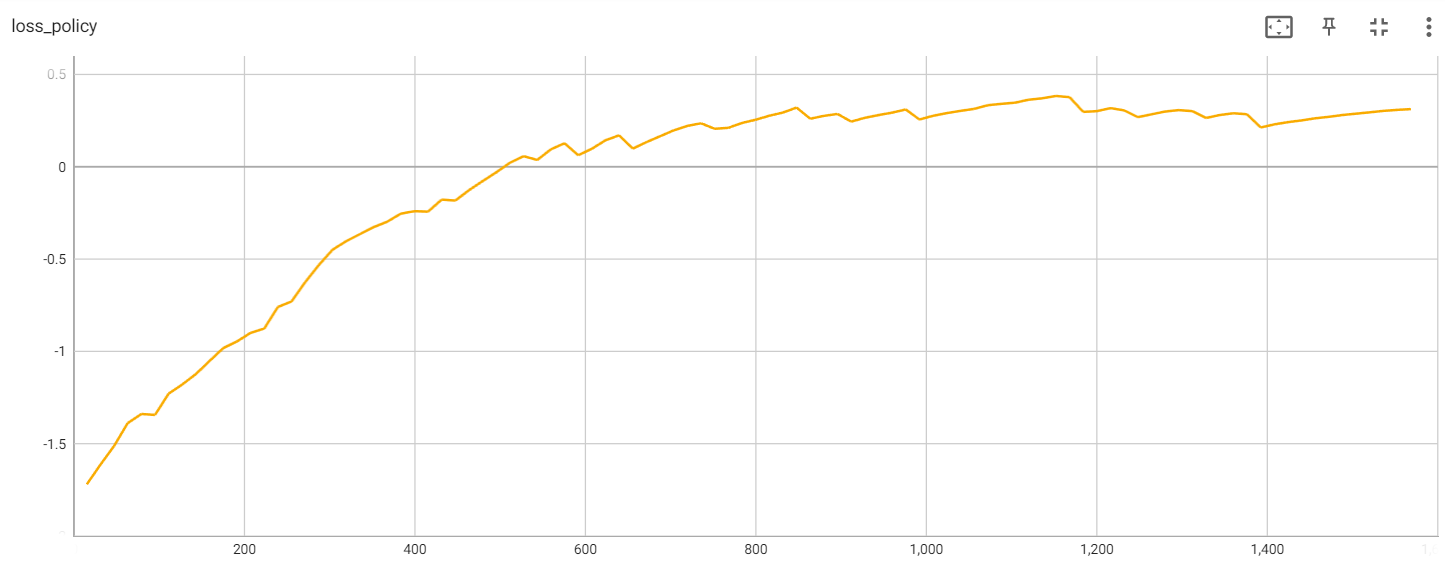
Policy loss
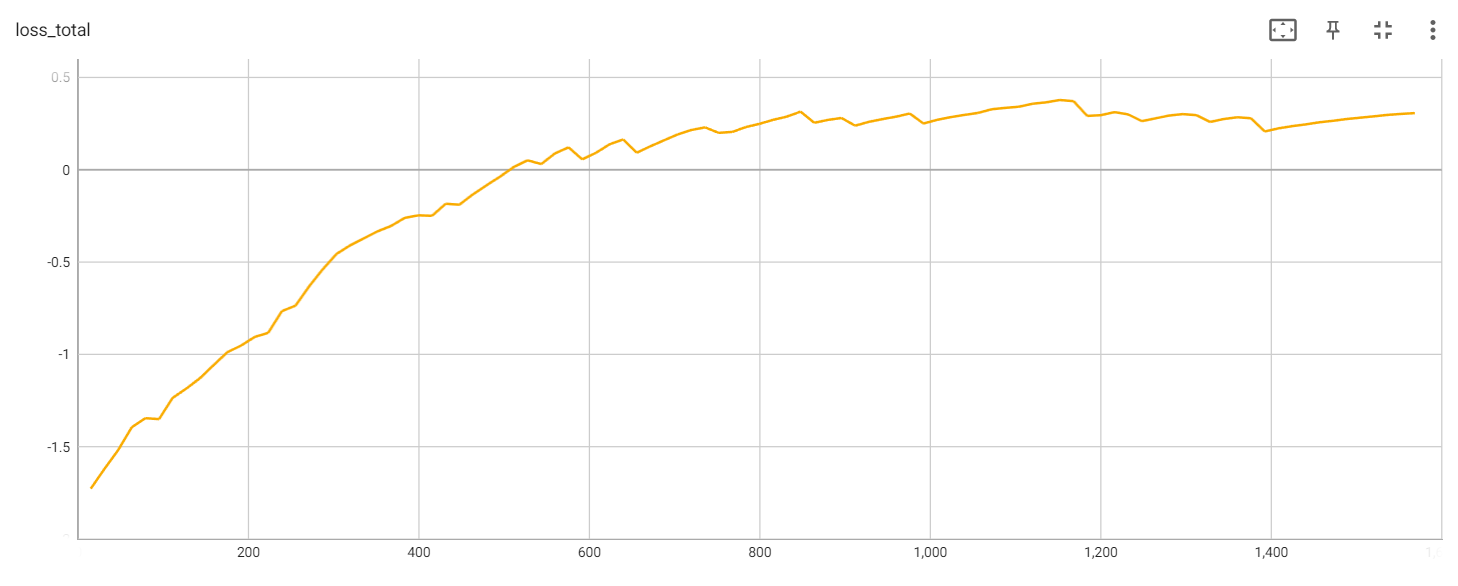
Total loss
从Loss结果看,这次实验并不理想,可以多运行几次,得到更好的结果。
5. 前四个算法的总体结果对比
蓝线:DQN(01_cartpole_dqn.py)
黑线:REINFORCE(02_cartpole_reinforce.py)
红线:REINFORCE with Baseline(03_cartpole_reinforce_baseline.py)
黄线:策略梯度法(04_cartpole_pg.py)
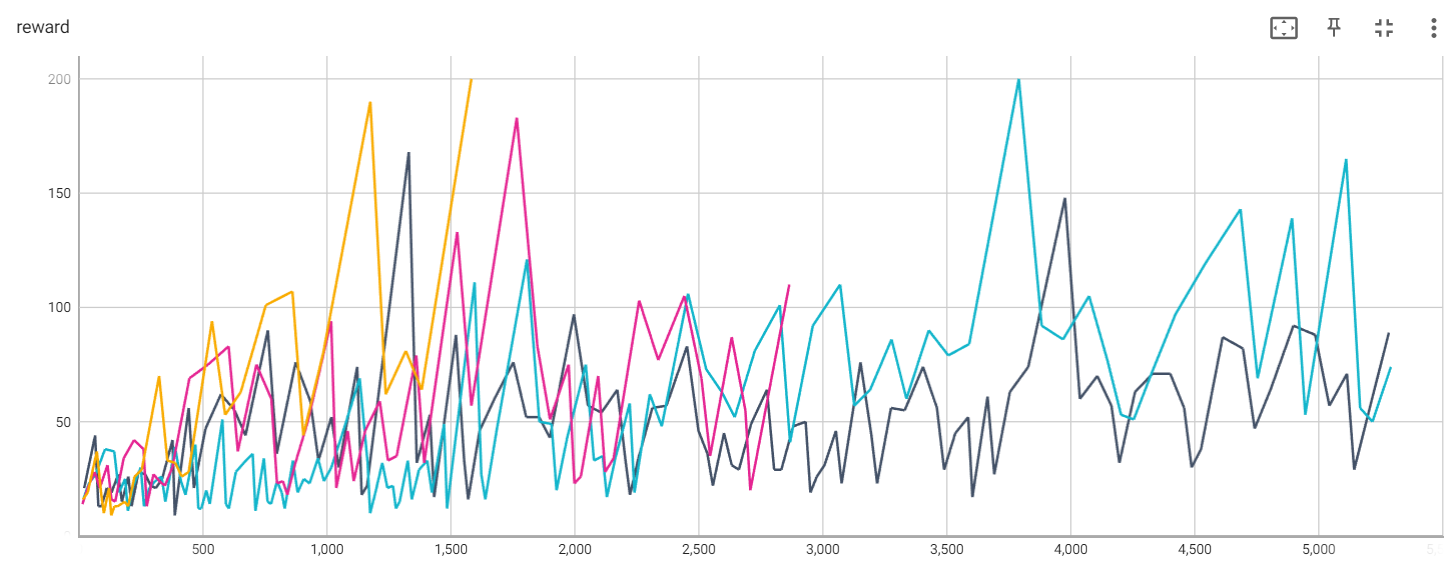
Reward
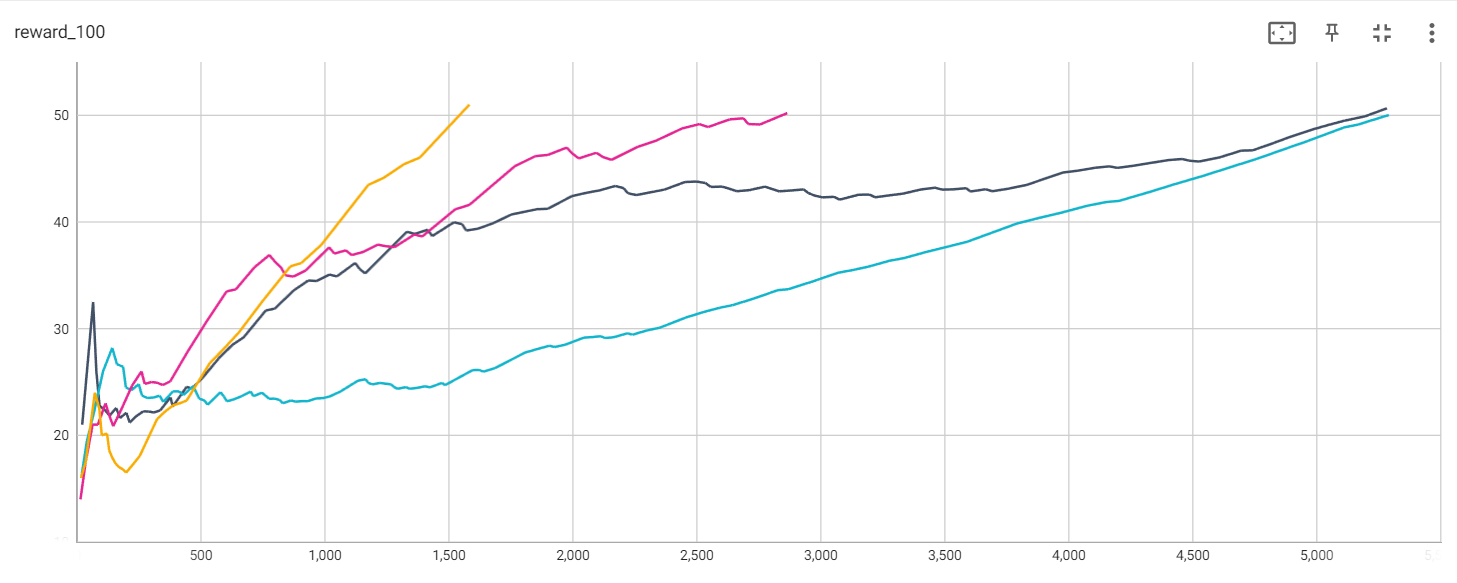
Average reward

Episodes
6. 06_cartpole_pg.py
6.1 程序
#!/usr/bin/env python3
# -*- coding=utf-8 -*-
# Policy gradient methods on CartPole
# 为增加探索,引入entropy bonus(信息熵正则项)
# 为了鼓励模型加入更多的不确定性,这样在训练的时候,模型就会去探索更多的可能性
# H(π) = - sum(π(a|s) * log π(a|s))
# 与03 Policy Gradients/04_cartpole_pg.py基本一致,唯一不同是Baseline可选择,加或者不加
# 加:min -(the discounted reward - baseline) * log π(s, a) + beta * sum (π(s, a) * log π(s, a))
# 不加:min -(the discounted reward) * log π(s, a) + beta * sum (π(s, a) * log π(s, a))
# https://www.cnblogs.com/kailugaji/
import gym
import ptan
import argparse
import numpy as np
from tensorboardX import SummaryWriter
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
GAMMA = 0.99 # 折扣率
LEARNING_RATE = 0.01 # 学习率
ENTROPY_BETA = 0.01 # 熵正则化因子 the scale of the entropy bonus
BATCH_SIZE = 16 # 一批xx个样本
REWARD_STEPS = 10
# 用于说明一条记录中包含的步(step)数 (sub-trajectories of length 10)
# how many steps ahead the Bellman equation is unrolled to estimate the discounted total reward of every transition.
# 构建网络
class PGN(nn.Module):
def __init__(self, input_size, n_actions):
# input_size:输入状态维度,hidden_size:隐层维度=128,n_actions:输出动作维度
super(PGN, self).__init__()
self.net = nn.Sequential(
nn.Linear(input_size, 128), # 全连接层,隐层预设为128维度
nn.ReLU(),
nn.Linear(128, n_actions) # 全连接层
)
def forward(self, x):
return self.net(x) # 未用softmax
if __name__ == "__main__":
parser = argparse.ArgumentParser()
parser.add_argument("--baseline", default=False, action='store_true', help="Enable mean baseline")
args = parser.parse_args()
args.baseline = "True" # 加baseline
env = gym.make("CartPole-v0") # 创建游戏环境
writer = SummaryWriter(comment="-cartpole-pg" + "-baseline=%s" % args.baseline)
net = PGN(env.observation_space.shape[0], env.action_space.n) # 4(状态)->128->2(动作)
# print(net)
agent = ptan.agent.PolicyAgent(net, preprocessor=ptan.agent.float32_preprocessor, apply_softmax=True)
# PolicyAgent:连续
# make a decision about actions for every observation (依概率)
# apply_softmax=True:网络输出先经过softmax转化成概率,再从这个概率分布中进行随机抽样
# float32_preprocessor:returns the observation as float64 instead of the float32 required by PyTorch
exp_source = ptan.experience.ExperienceSourceFirstLast(env, agent, gamma=GAMMA, steps_count=REWARD_STEPS)
# 返回运行记录以用于训练模型,输出格式为:(state, action, reward, last_state)
# 并不会输出每一步的信息,而是把多步的交互结果综合(累计多步的reward;显示头尾的状态)到一条Experience输出
# 多步rewards的累加是有衰退的,而其中的衰退系数由参数gamma(折扣率)指定,即reward=r1+gamma∗r2+(gamma^2)∗r3
# 其中rn代表第n步操作获得的reward
# last_state: the state we've got after executing the action. If our episode ends, we have None here
# steps_count=REWARD_STEPS:unroll the Bellman equation for 10 steps
optimizer = optim.Adam(net.parameters(), lr=LEARNING_RATE) # Adam优化
total_rewards = [] # 前几局的奖励之和
step_rewards = []
step_idx = 0 # 迭代次数/轮数
done_episodes = 0 # 局数,几局游戏
reward_sum = 0.0 # the sum of the discounted reward for every transition
batch_states, batch_actions, batch_scales = [], [], []
for step_idx, exp in enumerate(exp_source): # (state, action, reward, last_state)
reward_sum += exp.reward # the sum of the discounted reward for every transition
baseline = reward_sum / (step_idx + 1) # 奖励除以迭代次数(步数) the baseline for the policy scale
writer.add_scalar("baseline", baseline, step_idx)
batch_states.append(exp.state) # 状态
batch_actions.append(int(exp.action)) # 动作
if args.baseline: # True
batch_scales.append(exp.reward - baseline) # 优势函数,引入基准
else: # False
batch_scales.append(exp.reward) # 没有基准
# handle new rewards
new_rewards = exp_source.pop_total_rewards() # 返回一局游戏过后的total_rewords
if new_rewards:
done_episodes += 1 # 游戏局数(回合数)
reward = new_rewards[0] # 本局游戏奖励
total_rewards.append(reward) # 前几局的奖励之和
mean_rewards = float(np.mean(total_rewards[-100:])) # 平均奖励:前几局的奖励之和/回合数
print("第%d次: 第%d局游戏结束, 奖励为%6.2f, 平均奖励为%6.2f" % (step_idx, done_episodes, reward, mean_rewards))
writer.add_scalar("reward", reward, step_idx) # 本局游戏奖励
writer.add_scalar("reward_100", mean_rewards, step_idx) # 前几局游戏的平均奖励
writer.add_scalar("episodes", done_episodes, step_idx) # 游戏局数(回合数)
if mean_rewards > 50: # 最大期望奖励阈值,只有当mean_rewards > 50时才结束游戏
print("经过%d轮完成%d局游戏!" % (step_idx, done_episodes))
break
if len(batch_states) < BATCH_SIZE: # state里面还没超过BATCH_SIZE个样本
continue
states_v = torch.FloatTensor(batch_states)
batch_actions_t = torch.LongTensor(batch_actions)
batch_scale_v = torch.FloatTensor(batch_scales) # r 或者 优势函数(r - b)
# train
optimizer.zero_grad()
logits_v = net(states_v) # 输入状态,输出Q(s, a)值
log_prob_v = F.log_softmax(logits_v, dim=1) # 输出动作的对数概率分布 log π(s, a)
log_prob_actions_v = batch_scale_v * log_prob_v[range(BATCH_SIZE), batch_actions_t]
# 加基准:max (the discounted reward - baseline) * log π(s, a)
# 不加基准:max (the discounted reward) * log π(s, a)
loss_policy_v = -log_prob_actions_v.mean() # min
loss_policy_v.backward(retain_graph=True)
grads = np.concatenate([p.grad.data.numpy().flatten()
for p in net.parameters()
if p.grad is not None])
# add the entropy bonus to the loss
prob_v = F.softmax(logits_v, dim=1) # 输出动作的概率分布π(s, a)
entropy_v = -(prob_v * log_prob_v).sum(dim=1).mean() # 熵正则项
# 信息熵的计算公式:entropy = -sum (π(s, a) * log π(s, a))
entropy_loss_v = -ENTROPY_BETA * entropy_v # loss = - beta * entropy
entropy_loss_v.backward()
optimizer.step()
loss_v = loss_policy_v + entropy_loss_v
# 加基准:min -(the discounted reward - baseline) * log π(s, a) + beta * sum (π(s, a) * log π(s, a))
# 不加:min -(the discounted reward) * log π(s, a) + beta * sum (π(s, a) * log π(s, a))
# calculate the Kullback-Leibler (KL) divergence between the new policy and the old policy
new_logits_v = net(states_v) # 输入状态,输出Q(s, a)值
new_prob_v = F.softmax(new_logits_v, dim=1) # 输出动作的概率分布π(s, a)
kl_div_v = -((new_prob_v / prob_v).log() * prob_v).sum(dim=1).mean()
# KL散度的计算公式:KL = - sum(log(π'(s, a)/π(s, a)) * π(s, a))
writer.add_scalar("kl", kl_div_v.item(), step_idx)
writer.add_scalar("baseline", baseline, step_idx)
writer.add_scalar("entropy", entropy_v.item(), step_idx)
writer.add_scalar("batch_scales", np.mean(batch_scales), step_idx)
writer.add_scalar("loss_entropy", entropy_loss_v.item(), step_idx)
writer.add_scalar("loss_policy", loss_policy_v.item(), step_idx)
writer.add_scalar("loss_total", loss_v.item(), step_idx)
# calculate the statistics about the gradients on this training step
g_l2 = np.sqrt(np.mean(np.square(grads))) # L2 norm of gradients
g_max = np.max(np.abs(grads)) # the graph of the maximum
writer.add_scalar("grad_l2", g_l2, step_idx)
writer.add_scalar("grad_max", g_max, step_idx)
writer.add_scalar("grad_var", np.var(grads), step_idx) # 梯度方差
batch_states.clear()
batch_actions.clear()
batch_scales.clear()
writer.close()
6.2 结果
当不加baseline时:
第32次: 第1局游戏结束, 奖励为 32.00, 平均奖励为 32.00 第47次: 第2局游戏结束, 奖励为 15.00, 平均奖励为 23.50 第65次: 第3局游戏结束, 奖励为 18.00, 平均奖励为 21.67 第74次: 第4局游戏结束, 奖励为 9.00, 平均奖励为 18.50 第87次: 第5局游戏结束, 奖励为 13.00, 平均奖励为 17.40 第101次: 第6局游戏结束, 奖励为 14.00, 平均奖励为 16.83 第113次: 第7局游戏结束, 奖励为 12.00, 平均奖励为 16.14 第124次: 第8局游戏结束, 奖励为 11.00, 平均奖励为 15.50 第138次: 第9局游戏结束, 奖励为 14.00, 平均奖励为 15.33 第148次: 第10局游戏结束, 奖励为 10.00, 平均奖励为 14.80 第159次: 第11局游戏结束, 奖励为 11.00, 平均奖励为 14.45 第170次: 第12局游戏结束, 奖励为 11.00, 平均奖励为 14.17 第181次: 第13局游戏结束, 奖励为 11.00, 平均奖励为 13.92 第200次: 第14局游戏结束, 奖励为 19.00, 平均奖励为 14.29 第210次: 第15局游戏结束, 奖励为 10.00, 平均奖励为 14.00 第225次: 第16局游戏结束, 奖励为 15.00, 平均奖励为 14.06 第238次: 第17局游戏结束, 奖励为 13.00, 平均奖励为 14.00 第250次: 第18局游戏结束, 奖励为 12.00, 平均奖励为 13.89 第262次: 第19局游戏结束, 奖励为 12.00, 平均奖励为 13.79 第275次: 第20局游戏结束, 奖励为 13.00, 平均奖励为 13.75 第288次: 第21局游戏结束, 奖励为 13.00, 平均奖励为 13.71 第302次: 第22局游戏结束, 奖励为 14.00, 平均奖励为 13.73 第323次: 第23局游戏结束, 奖励为 21.00, 平均奖励为 14.04 第339次: 第24局游戏结束, 奖励为 16.00, 平均奖励为 14.12 第358次: 第25局游戏结束, 奖励为 19.00, 平均奖励为 14.32 第369次: 第26局游戏结束, 奖励为 11.00, 平均奖励为 14.19 第384次: 第27局游戏结束, 奖励为 15.00, 平均奖励为 14.22 第404次: 第28局游戏结束, 奖励为 20.00, 平均奖励为 14.43 第428次: 第29局游戏结束, 奖励为 24.00, 平均奖励为 14.76 第444次: 第30局游戏结束, 奖励为 16.00, 平均奖励为 14.80 第457次: 第31局游戏结束, 奖励为 13.00, 平均奖励为 14.74 第475次: 第32局游戏结束, 奖励为 18.00, 平均奖励为 14.84 第497次: 第33局游戏结束, 奖励为 22.00, 平均奖励为 15.06 第511次: 第34局游戏结束, 奖励为 14.00, 平均奖励为 15.03 第534次: 第35局游戏结束, 奖励为 23.00, 平均奖励为 15.26 第579次: 第36局游戏结束, 奖励为 45.00, 平均奖励为 16.08 第600次: 第37局游戏结束, 奖励为 21.00, 平均奖励为 16.22 第623次: 第38局游戏结束, 奖励为 23.00, 平均奖励为 16.39 第650次: 第39局游戏结束, 奖励为 27.00, 平均奖励为 16.67 第667次: 第40局游戏结束, 奖励为 17.00, 平均奖励为 16.68 第718次: 第41局游戏结束, 奖励为 51.00, 平均奖励为 17.51 第746次: 第42局游戏结束, 奖励为 28.00, 平均奖励为 17.76 第792次: 第43局游戏结束, 奖励为 46.00, 平均奖励为 18.42 第834次: 第44局游戏结束, 奖励为 42.00, 平均奖励为 18.95 第882次: 第45局游戏结束, 奖励为 48.00, 平均奖励为 19.60 第923次: 第46局游戏结束, 奖励为 41.00, 平均奖励为 20.07 第953次: 第47局游戏结束, 奖励为 30.00, 平均奖励为 20.28 第983次: 第48局游戏结束, 奖励为 30.00, 平均奖励为 20.48 第1071次: 第49局游戏结束, 奖励为 88.00, 平均奖励为 21.86 第1160次: 第50局游戏结束, 奖励为 89.00, 平均奖励为 23.20 第1287次: 第51局游戏结束, 奖励为127.00, 平均奖励为 25.24 第1367次: 第52局游戏结束, 奖励为 80.00, 平均奖励为 26.29 第1469次: 第53局游戏结束, 奖励为102.00, 平均奖励为 27.72 第1533次: 第54局游戏结束, 奖励为 64.00, 平均奖励为 28.39 第1589次: 第55局游戏结束, 奖励为 56.00, 平均奖励为 28.89 第1618次: 第56局游戏结束, 奖励为 29.00, 平均奖励为 28.89 第1651次: 第57局游戏结束, 奖励为 33.00, 平均奖励为 28.96 第1697次: 第58局游戏结束, 奖励为 46.00, 平均奖励为 29.26 第1707次: 第59局游戏结束, 奖励为 10.00, 平均奖励为 28.93 第1747次: 第60局游戏结束, 奖励为 40.00, 平均奖励为 29.12 第1778次: 第61局游戏结束, 奖励为 31.00, 平均奖励为 29.15 第1802次: 第62局游戏结束, 奖励为 24.00, 平均奖励为 29.06 第1820次: 第63局游戏结束, 奖励为 18.00, 平均奖励为 28.89 第1850次: 第64局游戏结束, 奖励为 30.00, 平均奖励为 28.91 第1862次: 第65局游戏结束, 奖励为 12.00, 平均奖励为 28.65 第1883次: 第66局游戏结束, 奖励为 21.00, 平均奖励为 28.53 第1919次: 第67局游戏结束, 奖励为 36.00, 平均奖励为 28.64 第1971次: 第68局游戏结束, 奖励为 52.00, 平均奖励为 28.99 第1996次: 第69局游戏结束, 奖励为 25.00, 平均奖励为 28.93 第2029次: 第70局游戏结束, 奖励为 33.00, 平均奖励为 28.99 第2104次: 第71局游戏结束, 奖励为 75.00, 平均奖励为 29.63 第2177次: 第72局游戏结束, 奖励为 73.00, 平均奖励为 30.24 第2270次: 第73局游戏结束, 奖励为 93.00, 平均奖励为 31.10 第2363次: 第74局游戏结束, 奖励为 93.00, 平均奖励为 31.93 第2530次: 第75局游戏结束, 奖励为167.00, 平均奖励为 33.73 第2608次: 第76局游戏结束, 奖励为 78.00, 平均奖励为 34.32 第2703次: 第77局游戏结束, 奖励为 95.00, 平均奖励为 35.10 第2854次: 第78局游戏结束, 奖励为151.00, 平均奖励为 36.59 第3054次: 第79局游戏结束, 奖励为200.00, 平均奖励为 38.66 第3152次: 第80局游戏结束, 奖励为 98.00, 平均奖励为 39.40 第3205次: 第81局游戏结束, 奖励为 53.00, 平均奖励为 39.57 第3228次: 第82局游戏结束, 奖励为 23.00, 平均奖励为 39.37 第3258次: 第83局游戏结束, 奖励为 30.00, 平均奖励为 39.25 第3279次: 第84局游戏结束, 奖励为 21.00, 平均奖励为 39.04 第3301次: 第85局游戏结束, 奖励为 22.00, 平均奖励为 38.84 第3328次: 第86局游戏结束, 奖励为 27.00, 平均奖励为 38.70 第3346次: 第87局游戏结束, 奖励为 18.00, 平均奖励为 38.46 第3366次: 第88局游戏结束, 奖励为 20.00, 平均奖励为 38.25 第3384次: 第89局游戏结束, 奖励为 18.00, 平均奖励为 38.02 第3399次: 第90局游戏结束, 奖励为 15.00, 平均奖励为 37.77 第3420次: 第91局游戏结束, 奖励为 21.00, 平均奖励为 37.58 第3440次: 第92局游戏结束, 奖励为 20.00, 平均奖励为 37.39 第3466次: 第93局游戏结束, 奖励为 26.00, 平均奖励为 37.27 第3489次: 第94局游戏结束, 奖励为 23.00, 平均奖励为 37.12 第3506次: 第95局游戏结束, 奖励为 17.00, 平均奖励为 36.91 第3531次: 第96局游戏结束, 奖励为 25.00, 平均奖励为 36.78 第3563次: 第97局游戏结束, 奖励为 32.00, 平均奖励为 36.73 第3592次: 第98局游戏结束, 奖励为 29.00, 平均奖励为 36.65 第3617次: 第99局游戏结束, 奖励为 25.00, 平均奖励为 36.54 第3678次: 第100局游戏结束, 奖励为 61.00, 平均奖励为 36.78 第3734次: 第101局游戏结束, 奖励为 56.00, 平均奖励为 37.02 第3814次: 第102局游戏结束, 奖励为 80.00, 平均奖励为 37.67 第3987次: 第103局游戏结束, 奖励为173.00, 平均奖励为 39.22 第4106次: 第104局游戏结束, 奖励为119.00, 平均奖励为 40.32 第4153次: 第105局游戏结束, 奖励为 47.00, 平均奖励为 40.66 第4229次: 第106局游戏结束, 奖励为 76.00, 平均奖励为 41.28 第4365次: 第107局游戏结束, 奖励为136.00, 平均奖励为 42.52 第4470次: 第108局游戏结束, 奖励为105.00, 平均奖励为 43.46 第4532次: 第109局游戏结束, 奖励为 62.00, 平均奖励为 43.94 第4588次: 第110局游戏结束, 奖励为 56.00, 平均奖励为 44.40 第4669次: 第111局游戏结束, 奖励为 81.00, 平均奖励为 45.10 第4736次: 第112局游戏结束, 奖励为 67.00, 平均奖励为 45.66 第4797次: 第113局游戏结束, 奖励为 61.00, 平均奖励为 46.16 第4890次: 第114局游戏结束, 奖励为 93.00, 平均奖励为 46.90 第4980次: 第115局游戏结束, 奖励为 90.00, 平均奖励为 47.70 第5050次: 第116局游戏结束, 奖励为 70.00, 平均奖励为 48.25 第5089次: 第117局游戏结束, 奖励为 39.00, 平均奖励为 48.51 第5140次: 第118局游戏结束, 奖励为 51.00, 平均奖励为 48.90 第5176次: 第119局游戏结束, 奖励为 36.00, 平均奖励为 49.14 第5207次: 第120局游戏结束, 奖励为 31.00, 平均奖励为 49.32 第5240次: 第121局游戏结束, 奖励为 33.00, 平均奖励为 49.52 第5278次: 第122局游戏结束, 奖励为 38.00, 平均奖励为 49.76 第5307次: 第123局游戏结束, 奖励为 29.00, 平均奖励为 49.84 第5351次: 第124局游戏结束, 奖励为 44.00, 平均奖励为 50.12 经过5351轮完成124局游戏!
当添加baseline时:
第18次: 第1局游戏结束, 奖励为 18.00, 平均奖励为 18.00 第36次: 第2局游戏结束, 奖励为 18.00, 平均奖励为 18.00 第58次: 第3局游戏结束, 奖励为 22.00, 平均奖励为 19.33 第80次: 第4局游戏结束, 奖励为 22.00, 平均奖励为 20.00 第92次: 第5局游戏结束, 奖励为 12.00, 平均奖励为 18.40 第116次: 第6局游戏结束, 奖励为 24.00, 平均奖励为 19.33 第187次: 第7局游戏结束, 奖励为 71.00, 平均奖励为 26.71 第228次: 第8局游戏结束, 奖励为 41.00, 平均奖励为 28.50 第253次: 第9局游戏结束, 奖励为 25.00, 平均奖励为 28.11 第276次: 第10局游戏结束, 奖励为 23.00, 平均奖励为 27.60 第352次: 第11局游戏结束, 奖励为 76.00, 平均奖励为 32.00 第459次: 第12局游戏结束, 奖励为107.00, 平均奖励为 38.25 第514次: 第13局游戏结束, 奖励为 55.00, 平均奖励为 39.54 第557次: 第14局游戏结束, 奖励为 43.00, 平均奖励为 39.79 第659次: 第15局游戏结束, 奖励为102.00, 平均奖励为 43.93 第859次: 第16局游戏结束, 奖励为200.00, 平均奖励为 53.69 经过859轮完成16局游戏!
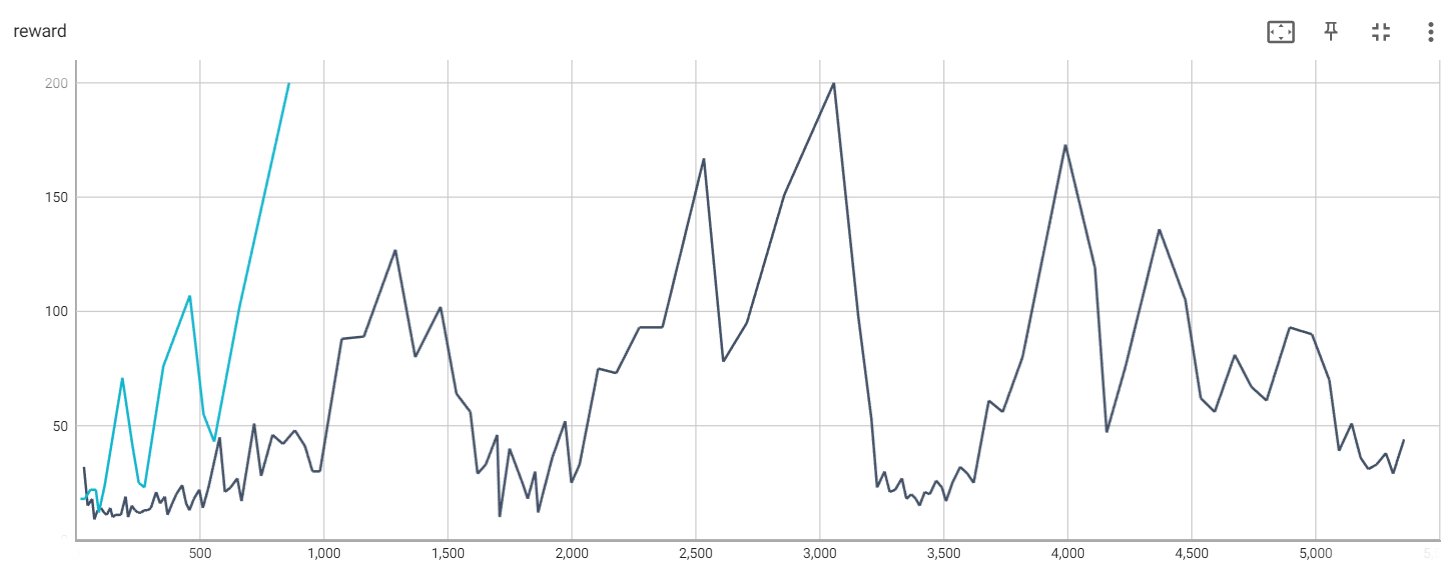
The rewards of training episodes without the baseline (black) and with the baseline (blue)
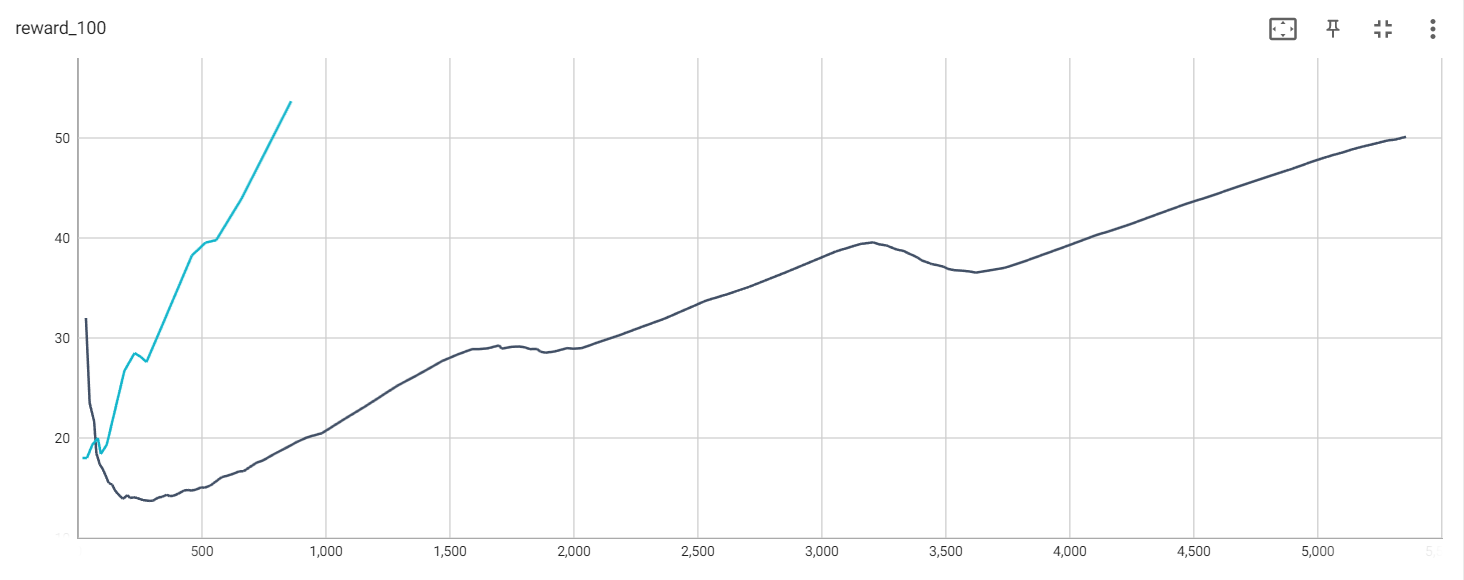
The average rewards of training episodes without the baseline (black) and with the baseline (blue)

Total loss without the baseline (black) and with the baseline (blue)
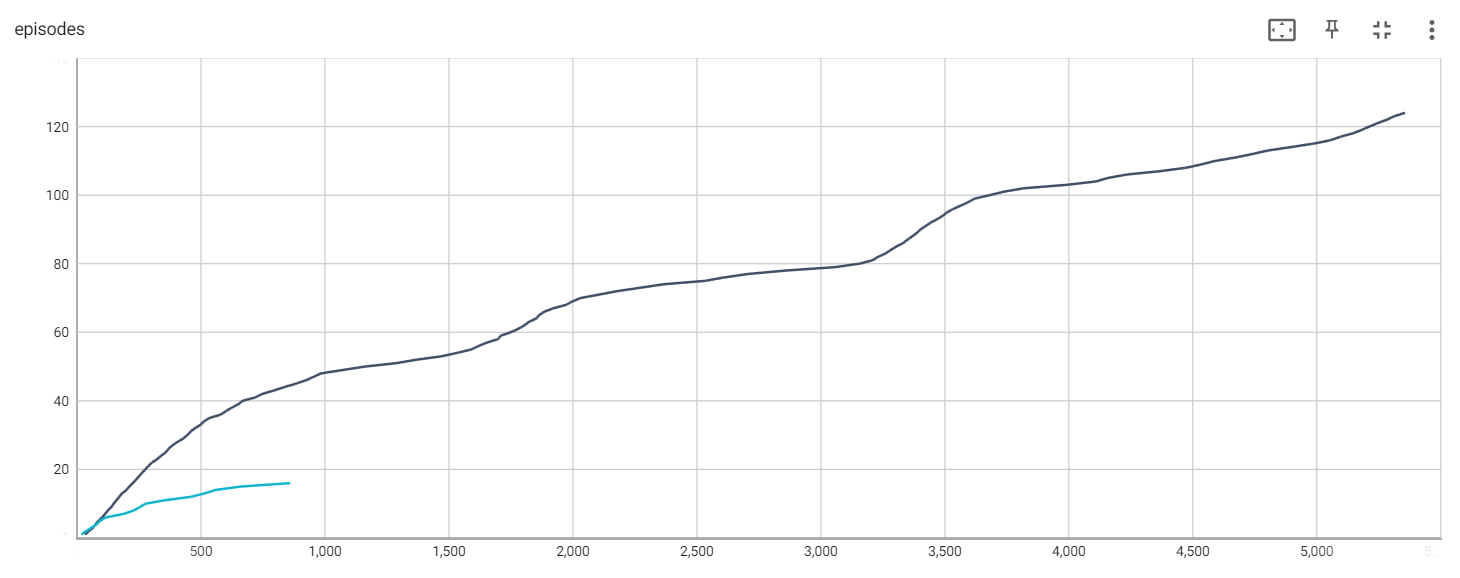
Episodes without the baseline (black) and with the baseline (blue)
打开tensorboard:
activate RL cd .. D: cd D:\xxx\Deep-Reinforcement-Learning-Hands-On-Second-Edition-master\Chapter11 tensorboard --logdir=./runs http://localhost:6006/
7. 参考文献
[1] https://github.com/PacktPublishing/Deep-Reinforcement-Learning-Hands-On-Second-Edition
[2] 强化学习(Reinforcement Learning) - 凯鲁嘎吉 - 博客园
[3] https://github.com/kailugaji/Hands-on-Reinforcement-Learning/tree/main/03%20Policy%20Gradients

