Deep Reinforcement Learning Hands-On——Higher-Level RL Libraries (PTAN)
作者:凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/
更多请看:Reinforcement Learning - 随笔分类 - 凯鲁嘎吉 - 博客园 https://www.cnblogs.com/kailugaji/category/2038931.html
这一篇博文参考了书目《Deep Reinforcement Learning Hands-On Second Edition》第7章内容,主要介绍一个高级强化学习库:PyTorch Agent Net (PTAN)。用Python从头实现DQN及其他强化学习算法是复杂的,代码量较大,而且不同算法可能会一次又一次地编写相同的代码,调试起来困难。PTAN库将常用的强化学习代码封装起来,从而简化代码量,便于调试。下面通过6个Python程序来学会使用PTAN。前5个程序告诉我们如何调用PTAN库函数,为第6个程序做铺垫,第6个程序以gym中的CartPole游戏为例,结合PTAN库实现DQN算法,这里只是简易版的DQN(网络架构不是三卷积两全连接,简化为两全连接)。DQN的算法流程参见:2.4.3 深度Q网络(Deep Q-Networks,DQN)
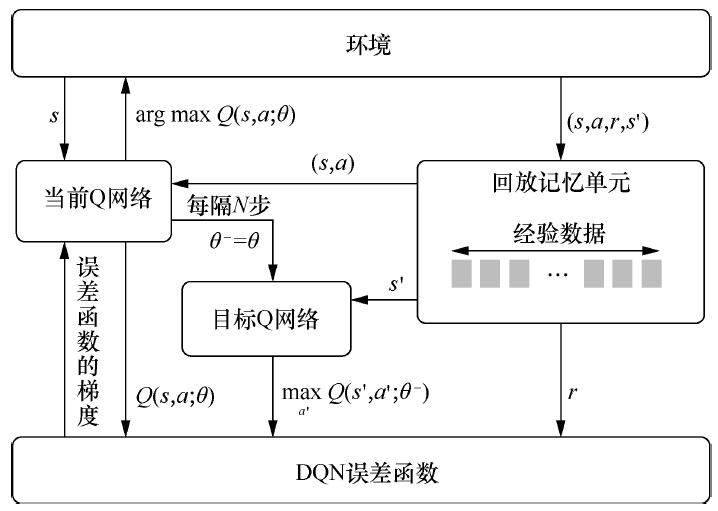
PTAN的详细代码见:https://github.com/Shmuma/ptan
PTAN的安装(PTAN需要与Torch匹配):
pip install torch==1.7.0+cpu torchvision==0.8.1+cpu torchaudio===0.7.0 -f https://download.pytorch.org/whl/torch_stable.html
pip install ptan
CartPole是推杆子游戏,争取让杆子立起来,有两个动作:向左和向右,有四个状态变量:小车在轨道上的位置,杆子与竖直方向的夹角,小车速度,角度变化率。杆子能越长时间保持平衡,得分越高。
1. 01_actions.py
1.1 程序
#!/usr/bin/env python3
# -*- coding=utf-8 -*-
# The PTAN library——Action selectors 动作选择器
# 从网络输出(Q值)到具体的动作值
# https://www.cnblogs.com/kailugaji/
import ptan
import numpy as np
if __name__ == "__main__":
print("方法1:基于值函数的方法 (网络输出的是Q值)")
q_vals_1 = np.array([
[1, 2, 3],
[1, -1, 0]
]) # 事先定义网络输出的Q值
print("Q值:\n", q_vals_1)
selector = ptan.actions.ArgmaxActionSelector()
print("具有最大Q值的动作索引:", selector(q_vals_1))
# 返回具有最大Q值的动作的索引——[列,行]
print("采用epsilon贪心策略的动作索引:")
selector = ptan.actions.EpsilonGreedyActionSelector(epsilon=0.0) # 以epsilon的概率随机选择值
print("当epsilon=0.0:", selector(q_vals_1)) # no random actions
selector.epsilon = 1.0 # will be random
print("当epsilon=1.0:", selector(q_vals_1))
selector.epsilon = 0.5
print("当epsilon=0.5:", selector(q_vals_1))
selector.epsilon = 0.1
print("当epsilon=0.1:", selector(q_vals_1))
print("-----------------------------------------------------")
print("方法2:基于策略函数的方法 (网络输出的是标准化概率分布)")
print("从三个概率分布中采样得到的动作:")
q_vals_2 = np.array([
[0.1, 0.8, 0.1], # 分布0 # 行归一化
[0.0, 0.0, 1.0], # 分布1
[0.5, 0.5, 0.0] # 分布2
]) # 事先定义网络输出的概率分布
# 从三个分布中进行抽样:
# 在第一个分布中,选择索引为1的动作的概率为80%
# 在第二个分布中,总是选择索引为2的动作
# 在第三个分布中,选择索引为0的动作和索引为1的动作是等可能的
selector = ptan.actions.ProbabilityActionSelector()
# 从概率分布中采样 (输入必须是一个标准化的概率分布)
for i in range(8): # 采样8次
acts = selector(q_vals_2)
print('第 %d 次: ' %(i+1), acts)
# acts的三个值分别是从三个分布中采样的动作的索引
# 可以看到第二个值始终是2,这是因为第二个分布中索引为2的动作的概率为1
1.2 结果
方法1:基于值函数的方法 (网络输出的是Q值) Q值: [[ 1 2 3] [ 1 -1 0]] 具有最大Q值的动作索引: [2 0] 采用epsilon贪心策略的动作索引: 当epsilon=0.0: [2 0] 当epsilon=1.0: [2 2] 当epsilon=0.5: [2 1] 当epsilon=0.1: [2 0] ----------------------------------------------------- 方法2:基于策略函数的方法 (网络输出的是标准化概率分布) 从三个概率分布中采样得到的动作: 第 1 次: [1 2 1] 第 2 次: [1 2 1] 第 3 次: [1 2 1] 第 4 次: [1 2 0] 第 5 次: [1 2 0] 第 6 次: [1 2 0] 第 7 次: [2 2 0] 第 8 次: [1 2 0]
2. 02_agents.py
2.1 程序
#!/usr/bin/env python3
# -*- coding=utf-8 -*-
# The PTAN library——The agent
# https://www.cnblogs.com/kailugaji/
import ptan
import torch
import torch.nn as nn
# 方法1:基于值函数的方法 (网络输出的是Q值)
# DQNAgent
class DQNNet(nn.Module):
def __init__(self, actions: int):
super(DQNNet, self).__init__()
self.actions = actions # 为简单起见,网络输出和输入一致, f(x)=x
def forward(self, x):
return torch.eye(x.size()[0], self.actions)
# 定义了返回对角线全1,其余部分全0的二维数组,大小为(batch_size=x.size()[0], actions)
# 方法2:基于策略函数的方法 (网络输出的是标准化概率分布)
# PolicyAgent
class PolicyNet(nn.Module):
def __init__(self, actions: int):
super(PolicyNet, self).__init__()
self.actions = actions # 为简单起见,网络输出和输入一致, f(x)=x
def forward(self, x):
# Now we produce the tensor with first two actions having the same logit scores
shape = (x.size()[0], self.actions) # 大小为(batch_size=x.size()[0], actions)
res = torch.zeros(shape, dtype=torch.float32)
res[:, 0] = 1
res[:, 1] = 1 # 定义了返回前两列为1,后面为0的二维数组
return res
if __name__ == "__main__":
net_1 = DQNNet(actions=3) # 3个动作(3列/3维)
print("方法1:基于值函数的方法 (网络输出的是Q值)")
net_in = torch.zeros(2, 10) # 输入2*10的全0矩阵,样本个数2,维度10
net_out = net_1(net_in)
print("DQN Net 输入:\n", net_in)
print("DQN Net 输出:\n", net_out)
# 得到对角线全1,其余部分全0的矩阵,大小为(batch_size=2, actions=3)
selector = ptan.actions.ArgmaxActionSelector()
agent = ptan.agent.DQNAgent(dqn_model=net_1, action_selector=selector)
# dqn_model换成自定义的DQNNet模型,action_selector保持不变,例子可见上一个程序01_actions.py
ag_in = torch.zeros(2, 5) # 输入:2*5的全0矩阵,样本个数2,维度5 (a batch of two observations, each having five values)
ag_out = agent(ag_in)
print("DQN网络输入:\n", ag_in)
print("具有最大Q值的动作与状态索引:", ag_out)
# 输出动作与状态的索引
# 1. 动作矩阵:网络输出中对应于1的动作索引,有2个样本,因此结果矩阵大小为1*2
# 2. 状态列表:由于例子未涉及状态,因此为None
print("采用epsilon贪心策略得到的动作索引:")
selector = ptan.actions.EpsilonGreedyActionSelector(epsilon=0.0) # no random actions
agent = ptan.agent.DQNAgent(dqn_model=net_1, action_selector=selector)
ag_in = torch.zeros(10, 5) # 输入:10*5的全0矩阵,10个样本
ag_out = agent(ag_in)[0] # [0]表示只返回动作的索引,不返回状态的索引
print("当epsilon=0:", ag_out) # DQNNet中actions=3使得第4维及后面索引全为0
selector.epsilon = 1.0 # 当epsilon为1时,所有的动作都是随机的,与网络的输出无关
ag_out = agent(ag_in)[0]
print("当epsilon=1:", ag_out)
selector.epsilon = 0.5
ag_out = agent(ag_in)[0]
print("当epsilon=0.5:", ag_out)
selector.epsilon = 0.1
ag_out = agent(ag_in)[0]
print("当epsilon=0.1:", ag_out)
print("----------------------------------------------------------------")
net_2 = PolicyNet(actions=5) # 5个动作(5列),0-4
print("方法2:基于策略函数的方法 (网络输出的是标准化概率分布)")
net_in = torch.zeros(6, 10) # 输入:6*10的全0矩阵,6个样本
net_out = net_2(net_in)
print("Policy Net 输入:\n", net_in)
print("Policy Net 输出:\n", net_out)
selector = ptan.actions.ProbabilityActionSelector()
agent = ptan.agent.PolicyAgent(model=net_2, action_selector=selector, apply_softmax=True)
# 对输出再采用softmax将数值归一化为[0, 1]的概率分布值
ag_in = torch.zeros(6, 5) # 输入:6*5的全0矩阵,6个样本
ag_out = agent(ag_in)[0]
print("Policy网络输入:\n", ag_in)
print("采样Policy方法得到的动作索引:", ag_out)
# 采样索引为2-4的动作概率小于0与1
2.2 结果
方法1:基于值函数的方法 (网络输出的是Q值)
DQN Net 输入:
tensor([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]])
DQN Net 输出:
tensor([[1., 0., 0.],
[0., 1., 0.]])
DQN网络输入:
tensor([[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]])
具有最大Q值的动作与状态索引: (array([0, 1], dtype=int64), [None, None])
采用epsilon贪心策略得到的动作索引:
当epsilon=0: [0 1 2 0 0 0 0 0 0 0]
当epsilon=1: [1 1 0 2 1 0 2 0 0 0]
当epsilon=0.5: [2 2 2 0 0 1 0 0 0 0]
当epsilon=0.1: [0 1 2 0 0 0 0 0 0 0]
----------------------------------------------------------------
方法2:基于策略函数的方法 (网络输出的是标准化概率分布)
Policy Net 输入:
tensor([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]])
Policy Net 输出:
tensor([[1., 1., 0., 0., 0.],
[1., 1., 0., 0., 0.],
[1., 1., 0., 0., 0.],
[1., 1., 0., 0., 0.],
[1., 1., 0., 0., 0.],
[1., 1., 0., 0., 0.]])
Policy网络输入:
tensor([[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]])
采样Policy方法得到的动作索引: [2 2 0 4 4 4]
3. 03_exp_sources.py
3.1 程序
#!/usr/bin/env python3
# -*- coding=utf-8 -*-
# The PTAN library——Experience source
# 是对智能体在环境中运行过程的一种封装,屏蔽了很多运行细节,最终只返回运行记录以用于训练模型
# 常用的两个封装类有:ExperienceSource,ExperienceSourceFirstLast(推荐使用)
# 部分参考: https://blog.csdn.net/HJJ19881016/article/details/105743835/
# https://www.cnblogs.com/kailugaji/
import gym
import ptan
from typing import List, Optional, Tuple, Any
# 构建Environment
class ToyEnv(gym.Env):
"""
Environment with observation 0..4 and actions 0..2
Observations are rotated sequentialy mod 5, reward is equal to given action.
Episodes are having fixed length of 10
"""
def __init__(self):
super(ToyEnv, self).__init__()
self.observation_space = gym.spaces.Discrete(n=5) # integer observation, which increases from 0 to 4
self.action_space = gym.spaces.Discrete(n=3) # integer action, which increases from 0 to 2
self.step_index = 0
def reset(self): # 用于重置环境
self.step_index = 0
return self.step_index
def step(self, action):
# 输入:action
# 输出:observation, reward, done, info
# observation(object)一个特定的环境对象,代表了你从环境中得到的观测值
# reward(float)由于之前采取的动作所获得的大量奖励,与环境交互的过程中,奖励值的规模会发生变化,但是总体的目标一直都是使得总奖励最大
# done(boolean)决定是否将环境初始化,大多数,但不是所有的任务都被定义好了什么情况该结束这个回合
# info(dict)调试过程中将会产生的有用信息,有时它会对我们的强化学习学习过程很有用
is_done = self.step_index == 10 # 一局游戏走10步
if is_done:
return self.step_index % self.observation_space.n, 0.0, is_done, {}
# Observation: mod 5, 0-4一循环,依次递增
self.step_index += 1
reward = float(action)
return self.step_index % self.observation_space.n, reward, self.step_index == 10, {}
# 这里定义了reward = action,info = {}, 玩够10步done=True
# 构建Agent
# 继承BaseAgent来自定义自己的Agent类,通过重写__call__()方法来实现Obervation到action的转换逻辑
class DullAgent(ptan.agent.BaseAgent):
"""
Agent always returns the fixed action
"""
def __init__(self, action: int):
self.action = action
def __call__(self, observations: List[Any], state: Optional[List] = None) -> Tuple[List[int], Optional[List]]:
# "->"常常出现在python函数定义的函数名后面,为函数添加元数据,描述函数的返回类型,从而方便开发人员使用
# 不管observations输入的是什么,结果都是输入的action的值
return [self.action for _ in observations], state
if __name__ == "__main__":
print("案例I:")
env = ToyEnv()
s = env.reset()
print("env.reset() -> %s" % s)
s = env.step(1) # action = 1
print("env.step(1) -> %s" % str(s))
s = env.step(2) # action = 2
print("env.step(2) -> %s" % str(s))
# 输出:observation, reward, done, info
for i in range(10):
r = env.step(0) # action = 0
print("第 %d 次 env.step(0) -> %s" % (i, str(r)))
# 重复10次,action的索引为0
# 输出:observation, reward, done, info
print("-------------------------------------------------------------------")
print("案例II:")
agent = DullAgent(action=1) # 生成固定动作,与action的取值保持一致,与observations取值无关
print("agent:", agent(observations=[2, 1, 3, 1])[0])
# [1, 2]: observations
# [0]只输出动作索引
print("-------------------------------------------------------------------")
print("案例III:")
env = ToyEnv()
agent = DullAgent(action=1) # 生成固定动作,始终为1
print("1. ExperienceSource (steps_count=2): ")
exp_source_1 = ptan.experience.ExperienceSource(env, agent, steps_count=2)
# ExperienceSource输入:
# env: The Gym environment to be used. Alternatively, it could be the list of environments.
# agent: The agent instance.
# steps_count: 用于说明一条记录中包含的步(step)数 (sub-trajectories of length 2)
# ExperienceSource输出:
# 返回智能体在环境中每一步的交互信息,输出格式为:(state, action, reward, done)
# 其中state为agent所处的状态,action为采取的动作,reward为采取action后获得的即时奖励,done用来标识episode是否结束。
for idx, exp in enumerate(exp_source_1):
if idx > 15:
break
print("第%d步" %(idx), exp)
print("2. ExperienceSource (steps_count=4): ")
exp_source_2 = ptan.experience.ExperienceSource(env, agent, steps_count=4)
# print(next(iter(exp_source_2))) # 只一步
# iter()返回迭代器对象
# next()函数自动调用文件第一行并返回下一行
for idx, exp in enumerate(exp_source_2):
if exp[0].done:
break
print("第%d步" %(idx), exp)
print("3. ExperienceSource (steps_count=2): ")
exp_source_3 = ptan.experience.ExperienceSource([ToyEnv(), ToyEnv()], agent, steps_count=2)
# 环境正在以循环的方式迭代,从两个环境中一步步获取轨迹。
for idx, exp in enumerate(exp_source_3):
if idx > 20:
break
print("第%d步" %(idx), exp)
print("4. ExperienceSourceFirstLast (steps_count=1): ")
exp_source_4 = ptan.experience.ExperienceSourceFirstLast(env, agent, gamma=1.0, steps_count=1)
# 输出的信息格式为:(state, action, reward, last_state)
# 并不会输出每一步的信息,而是把多步的交互结果综合(累计多步的reward;显示头尾的状态)到一条Experience输出
# 多步rewards的累加是有衰退的,而其中的衰退系数由参数gamma(折扣率)指定,即reward=r1+gamma∗r2+(gamma^2)∗r3
# 其中rn代表第n步操作获得的reward
# last_state: the state we've got after executing the action. If our episode ends, we have None here
for idx, exp in enumerate(exp_source_4):
print("第%d步" %(idx), exp)
if idx > 10:
break
print("5. ExperienceSourceFirstLast (steps_count=4): ")
exp_source_5 = ptan.experience.ExperienceSourceFirstLast(env, agent, gamma=0.6, steps_count=4)
# 输出的信息格式为:(state, action, reward, last_state)
# 并不会输出每一步的信息,而是把多步的交互结果综合(累计多步的reward;显示头尾的状态)到一条Experience输出
# 多步rewards的累加是有衰退的,而其中的衰退系数由参数gamma指定,即reward=r1+gamma∗r2+(gamma^2)∗r3
# 其中rn代表第n步操作获得的reward
# last_state: the state we've got after executing the action. If our episode ends, we have None here
for idx, exp in enumerate(exp_source_5):
print("第%d步" % (idx), exp)
if idx > 10:
break
3.2 结果
案例I:
env.reset() -> 0
env.step(1) -> (1, 1.0, False, {})
env.step(2) -> (2, 2.0, False, {})
第 0 次 env.step(0) -> (3, 0.0, False, {})
第 1 次 env.step(0) -> (4, 0.0, False, {})
第 2 次 env.step(0) -> (0, 0.0, False, {})
第 3 次 env.step(0) -> (1, 0.0, False, {})
第 4 次 env.step(0) -> (2, 0.0, False, {})
第 5 次 env.step(0) -> (3, 0.0, False, {})
第 6 次 env.step(0) -> (4, 0.0, False, {})
第 7 次 env.step(0) -> (0, 0.0, True, {})
第 8 次 env.step(0) -> (0, 0.0, True, {})
第 9 次 env.step(0) -> (0, 0.0, True, {})
-------------------------------------------------------------------
案例II:
agent: [1, 1, 1, 1]
-------------------------------------------------------------------
案例III:
1. ExperienceSource (steps_count=2):
第0步 (Experience(state=0, action=1, reward=1.0, done=False), Experience(state=1, action=1, reward=1.0, done=False))
第1步 (Experience(state=1, action=1, reward=1.0, done=False), Experience(state=2, action=1, reward=1.0, done=False))
第2步 (Experience(state=2, action=1, reward=1.0, done=False), Experience(state=3, action=1, reward=1.0, done=False))
第3步 (Experience(state=3, action=1, reward=1.0, done=False), Experience(state=4, action=1, reward=1.0, done=False))
第4步 (Experience(state=4, action=1, reward=1.0, done=False), Experience(state=0, action=1, reward=1.0, done=False))
第5步 (Experience(state=0, action=1, reward=1.0, done=False), Experience(state=1, action=1, reward=1.0, done=False))
第6步 (Experience(state=1, action=1, reward=1.0, done=False), Experience(state=2, action=1, reward=1.0, done=False))
第7步 (Experience(state=2, action=1, reward=1.0, done=False), Experience(state=3, action=1, reward=1.0, done=False))
第8步 (Experience(state=3, action=1, reward=1.0, done=False), Experience(state=4, action=1, reward=1.0, done=True))
第9步 (Experience(state=4, action=1, reward=1.0, done=True),)
第10步 (Experience(state=0, action=1, reward=1.0, done=False), Experience(state=1, action=1, reward=1.0, done=False))
第11步 (Experience(state=1, action=1, reward=1.0, done=False), Experience(state=2, action=1, reward=1.0, done=False))
第12步 (Experience(state=2, action=1, reward=1.0, done=False), Experience(state=3, action=1, reward=1.0, done=False))
第13步 (Experience(state=3, action=1, reward=1.0, done=False), Experience(state=4, action=1, reward=1.0, done=False))
第14步 (Experience(state=4, action=1, reward=1.0, done=False), Experience(state=0, action=1, reward=1.0, done=False))
第15步 (Experience(state=0, action=1, reward=1.0, done=False), Experience(state=1, action=1, reward=1.0, done=False))
2. ExperienceSource (steps_count=4):
第0步 (Experience(state=0, action=1, reward=1.0, done=False), Experience(state=1, action=1, reward=1.0, done=False), Experience(state=2, action=1, reward=1.0, done=False), Experience(state=3, action=1, reward=1.0, done=False))
第1步 (Experience(state=1, action=1, reward=1.0, done=False), Experience(state=2, action=1, reward=1.0, done=False), Experience(state=3, action=1, reward=1.0, done=False), Experience(state=4, action=1, reward=1.0, done=False))
第2步 (Experience(state=2, action=1, reward=1.0, done=False), Experience(state=3, action=1, reward=1.0, done=False), Experience(state=4, action=1, reward=1.0, done=False), Experience(state=0, action=1, reward=1.0, done=False))
第3步 (Experience(state=3, action=1, reward=1.0, done=False), Experience(state=4, action=1, reward=1.0, done=False), Experience(state=0, action=1, reward=1.0, done=False), Experience(state=1, action=1, reward=1.0, done=False))
第4步 (Experience(state=4, action=1, reward=1.0, done=False), Experience(state=0, action=1, reward=1.0, done=False), Experience(state=1, action=1, reward=1.0, done=False), Experience(state=2, action=1, reward=1.0, done=False))
第5步 (Experience(state=0, action=1, reward=1.0, done=False), Experience(state=1, action=1, reward=1.0, done=False), Experience(state=2, action=1, reward=1.0, done=False), Experience(state=3, action=1, reward=1.0, done=False))
第6步 (Experience(state=1, action=1, reward=1.0, done=False), Experience(state=2, action=1, reward=1.0, done=False), Experience(state=3, action=1, reward=1.0, done=False), Experience(state=4, action=1, reward=1.0, done=True))
第7步 (Experience(state=2, action=1, reward=1.0, done=False), Experience(state=3, action=1, reward=1.0, done=False), Experience(state=4, action=1, reward=1.0, done=True))
第8步 (Experience(state=3, action=1, reward=1.0, done=False), Experience(state=4, action=1, reward=1.0, done=True))
3. ExperienceSource (steps_count=2):
第0步 (Experience(state=0, action=1, reward=1.0, done=False), Experience(state=1, action=1, reward=1.0, done=False))
第1步 (Experience(state=0, action=1, reward=1.0, done=False), Experience(state=1, action=1, reward=1.0, done=False))
第2步 (Experience(state=1, action=1, reward=1.0, done=False), Experience(state=2, action=1, reward=1.0, done=False))
第3步 (Experience(state=1, action=1, reward=1.0, done=False), Experience(state=2, action=1, reward=1.0, done=False))
第4步 (Experience(state=2, action=1, reward=1.0, done=False), Experience(state=3, action=1, reward=1.0, done=False))
第5步 (Experience(state=2, action=1, reward=1.0, done=False), Experience(state=3, action=1, reward=1.0, done=False))
第6步 (Experience(state=3, action=1, reward=1.0, done=False), Experience(state=4, action=1, reward=1.0, done=False))
第7步 (Experience(state=3, action=1, reward=1.0, done=False), Experience(state=4, action=1, reward=1.0, done=False))
第8步 (Experience(state=4, action=1, reward=1.0, done=False), Experience(state=0, action=1, reward=1.0, done=False))
第9步 (Experience(state=4, action=1, reward=1.0, done=False), Experience(state=0, action=1, reward=1.0, done=False))
第10步 (Experience(state=0, action=1, reward=1.0, done=False), Experience(state=1, action=1, reward=1.0, done=False))
第11步 (Experience(state=0, action=1, reward=1.0, done=False), Experience(state=1, action=1, reward=1.0, done=False))
第12步 (Experience(state=1, action=1, reward=1.0, done=False), Experience(state=2, action=1, reward=1.0, done=False))
第13步 (Experience(state=1, action=1, reward=1.0, done=False), Experience(state=2, action=1, reward=1.0, done=False))
第14步 (Experience(state=2, action=1, reward=1.0, done=False), Experience(state=3, action=1, reward=1.0, done=False))
第15步 (Experience(state=2, action=1, reward=1.0, done=False), Experience(state=3, action=1, reward=1.0, done=False))
第16步 (Experience(state=3, action=1, reward=1.0, done=False), Experience(state=4, action=1, reward=1.0, done=True))
第17步 (Experience(state=4, action=1, reward=1.0, done=True),)
第18步 (Experience(state=3, action=1, reward=1.0, done=False), Experience(state=4, action=1, reward=1.0, done=True))
第19步 (Experience(state=4, action=1, reward=1.0, done=True),)
第20步 (Experience(state=0, action=1, reward=1.0, done=False), Experience(state=1, action=1, reward=1.0, done=False))
4. ExperienceSourceFirstLast (steps_count=1):
第0步 ExperienceFirstLast(state=0, action=1, reward=1.0, last_state=1)
第1步 ExperienceFirstLast(state=1, action=1, reward=1.0, last_state=2)
第2步 ExperienceFirstLast(state=2, action=1, reward=1.0, last_state=3)
第3步 ExperienceFirstLast(state=3, action=1, reward=1.0, last_state=4)
第4步 ExperienceFirstLast(state=4, action=1, reward=1.0, last_state=0)
第5步 ExperienceFirstLast(state=0, action=1, reward=1.0, last_state=1)
第6步 ExperienceFirstLast(state=1, action=1, reward=1.0, last_state=2)
第7步 ExperienceFirstLast(state=2, action=1, reward=1.0, last_state=3)
第8步 ExperienceFirstLast(state=3, action=1, reward=1.0, last_state=4)
第9步 ExperienceFirstLast(state=4, action=1, reward=1.0, last_state=None)
第10步 ExperienceFirstLast(state=0, action=1, reward=1.0, last_state=1)
第11步 ExperienceFirstLast(state=1, action=1, reward=1.0, last_state=2)
5. ExperienceSourceFirstLast (steps_count=4):
第0步 ExperienceFirstLast(state=0, action=1, reward=2.176, last_state=4)
第1步 ExperienceFirstLast(state=1, action=1, reward=2.176, last_state=0)
第2步 ExperienceFirstLast(state=2, action=1, reward=2.176, last_state=1)
第3步 ExperienceFirstLast(state=3, action=1, reward=2.176, last_state=2)
第4步 ExperienceFirstLast(state=4, action=1, reward=2.176, last_state=3)
第5步 ExperienceFirstLast(state=0, action=1, reward=2.176, last_state=4)
第6步 ExperienceFirstLast(state=1, action=1, reward=2.176, last_state=None)
第7步 ExperienceFirstLast(state=2, action=1, reward=1.96, last_state=None)
第8步 ExperienceFirstLast(state=3, action=1, reward=1.6, last_state=None)
第9步 ExperienceFirstLast(state=4, action=1, reward=1.0, last_state=None)
第10步 ExperienceFirstLast(state=0, action=1, reward=2.176, last_state=4)
第11步 ExperienceFirstLast(state=1, action=1, reward=2.176, last_state=0)
4. 04_replay_buf.py
4.1 程序
#!/usr/bin/env python3
# -*- coding=utf-8 -*-
# The PTAN library——Experience replay buffers 经验回放池
# 在DQN中,很少处理即时的经验样本,因为它们是高度相关的,这导致了训练中的不稳定性
# 构建一个很大的经验回放池,其中填充了经验片段
# 然后对回放池进行采样(随机或带优先级权重),得到训练批。
# 经验回放池通常有最大容量,所以当经验回放池达到极限时,旧的样本将被推出。
# 训练时,随机从经验池中抽取样本来代替当前的样本用来进行训练。
# 这样,就打破了和相邻训练样本的相似性,避免模型陷入局部最优
# https://www.cnblogs.com/kailugaji/
import gym
import ptan
from typing import List, Optional, Tuple, Any
# 构建Environment
class ToyEnv(gym.Env):
"""
Environment with observation 0..4 and actions 0..2
Observations are rotated sequentialy mod 5, reward is equal to given action.
Episodes are having fixed length of 10
"""
def __init__(self):
super(ToyEnv, self).__init__()
self.observation_space = gym.spaces.Discrete(n=5) # integer observation, which increases from 0 to 4
self.action_space = gym.spaces.Discrete(n=3) # integer action, which increases from 0 to 2
self.step_index = 0
def reset(self):
self.step_index = 0
return self.step_index
def step(self, action):
# 输入:action
# 输出:observation, reward, done, info
is_done = self.step_index == 10 # 一局游戏走10步
if is_done:
return self.step_index % self.observation_space.n, 0.0, is_done, {}
self.step_index += 1
reward = float(action)
return self.step_index % self.observation_space.n, reward, self.step_index == 10, {}
# Observation: mod 5, 0-4一循环,依次递增
# 构建Agent
class DullAgent(ptan.agent.BaseAgent):
"""
Agent always returns the fixed action
"""
def __init__(self, action: int):
self.action = action
def __call__(self, observations: List[Any], state: Optional[List] = None) -> Tuple[List[int], Optional[List]]:
# 不管observations输入的是什么,结果都是输入的action的值
return [self.action for _ in observations], state
if __name__ == "__main__":
env = ToyEnv()
agent = DullAgent(action=1) # 生成固定动作,与action的取值保持一致,与observations取值无关
exp_source = ptan.experience.ExperienceSourceFirstLast(env, agent, gamma=1.0, steps_count=1)
# 输出的信息格式为:(state, action, reward, last_state)
buffer = ptan.experience.ExperienceReplayBuffer(exp_source, buffer_size=100)
# a simple replay buffer of predefined size with uniform sampling.
# 构建buffer,容量为100,当前没东西,len(buffer) = 0
for step in range(6): # 最大buffer进6个样本
buffer.populate(1) # 从环境中获取一个新样本
# The method populate(N) to get N samples from the experience source and put them into the buffer
print("第%d次buffer大小:" %step, len(buffer))
if len(buffer) < 5: # buffer里面还没超过5个样本
continue # if buffer is small enough (<5), do nothing
# buffer等于或超过5个后,从buffer里面均匀抽样一个批次的样本,一批4个样本
batch = buffer.sample(4) # The method sample(N) to get the batch of N experience objects
print("Train time, %d batch samples:" % len(batch))
for s in batch:
print(s)
4.2 结果
第0次buffer大小: 1 第1次buffer大小: 2 第2次buffer大小: 3 第3次buffer大小: 4 第4次buffer大小: 5 Train time, 4 batch samples: ExperienceFirstLast(state=0, action=1, reward=1.0, last_state=1) ExperienceFirstLast(state=1, action=1, reward=1.0, last_state=2) ExperienceFirstLast(state=0, action=1, reward=1.0, last_state=1) ExperienceFirstLast(state=3, action=1, reward=1.0, last_state=4) 第5次buffer大小: 6 Train time, 4 batch samples: ExperienceFirstLast(state=2, action=1, reward=1.0, last_state=3) ExperienceFirstLast(state=3, action=1, reward=1.0, last_state=4) ExperienceFirstLast(state=4, action=1, reward=1.0, last_state=0) ExperienceFirstLast(state=0, action=1, reward=1.0, last_state=1)
5. 05_target_net.py
5.1 程序
#!/usr/bin/env python3
# -*- coding=utf-8 -*-
# The PTAN library——The TargetNet class
# TargetNet允许我们同步具有相同架构的两个网络,其目的是为了提高训练稳定性
# https://www.cnblogs.com/kailugaji/
import ptan
import torch.nn as nn
# 创建网络
class DQNNet(nn.Module):
def __init__(self):
super(DQNNet, self).__init__()
self.ff = nn.Linear(5, 3) # in_features=5, out_features=3, 权重大小:(3, 5)
def forward(self, x):
return self.ff(x)
if __name__ == "__main__":
net = DQNNet()
print("原网络架构:\n", net)
tgt_net = ptan.agent.TargetNet(net)
print("原网络权重:", net.ff.weight)
print("目标网络权重:", tgt_net.target_model.ff.weight)
# 上述原网络与目标网络权重相同
# 然而,它们彼此独立,只是拥有相同的架构:
net.ff.weight.data += 1.0
print("-------------------------------------------------------------------")
print("更新后:")
print("原网络权重:", net.ff.weight)
print("目标网络权重:", tgt_net.target_model.ff.weight)
# 要再次同步它们,可以使用sync()方法
tgt_net.sync() # weights from the source network are copied into the target network
print("-------------------------------------------------------------------")
print("同步后:")
print("原网络权重:", net.ff.weight)
print("目标网络权重:", tgt_net.target_model.ff.weight)
5.2 结果
原网络架构:
DQNNet(
(ff): Linear(in_features=5, out_features=3, bias=True)
)
原网络权重: Parameter containing:
tensor([[-0.0103, 0.4268, 0.2549, 0.1492, 0.2748],
[ 0.0375, -0.0403, 0.0326, 0.0213, 0.1052],
[-0.1674, -0.3298, -0.0271, -0.1609, 0.3070]], requires_grad=True)
目标网络权重: Parameter containing:
tensor([[-0.0103, 0.4268, 0.2549, 0.1492, 0.2748],
[ 0.0375, -0.0403, 0.0326, 0.0213, 0.1052],
[-0.1674, -0.3298, -0.0271, -0.1609, 0.3070]], requires_grad=True)
-------------------------------------------------------------------
更新后:
原网络权重: Parameter containing:
tensor([[0.9897, 1.4268, 1.2549, 1.1492, 1.2748],
[1.0375, 0.9597, 1.0326, 1.0213, 1.1052],
[0.8326, 0.6702, 0.9729, 0.8391, 1.3070]], requires_grad=True)
目标网络权重: Parameter containing:
tensor([[-0.0103, 0.4268, 0.2549, 0.1492, 0.2748],
[ 0.0375, -0.0403, 0.0326, 0.0213, 0.1052],
[-0.1674, -0.3298, -0.0271, -0.1609, 0.3070]], requires_grad=True)
-------------------------------------------------------------------
同步后:
原网络权重: Parameter containing:
tensor([[0.9897, 1.4268, 1.2549, 1.1492, 1.2748],
[1.0375, 0.9597, 1.0326, 1.0213, 1.1052],
[0.8326, 0.6702, 0.9729, 0.8391, 1.3070]], requires_grad=True)
目标网络权重: Parameter containing:
tensor([[0.9897, 1.4268, 1.2549, 1.1492, 1.2748],
[1.0375, 0.9597, 1.0326, 1.0213, 1.1052],
[0.8326, 0.6702, 0.9729, 0.8391, 1.3070]], requires_grad=True)
6. 06_cartpole.py
6.1 程序
#!/usr/bin/env python3
# -*- coding=utf-8 -*-
# The PTAN library——The PTAN CartPole solver
# 前述5个程序全部是为了CartPole实战做准备
# https://www.cnblogs.com/kailugaji/
import gym
import ptan
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import matplotlib.pylab as plt
from matplotlib import rcParams
config = {
"font.family":'Times New Roman',
"font.size": 12,
"mathtext.fontset": 'stix',
"font.serif": ['SimSun']
}
rcParams.update(config)
HIDDEN_SIZE = 128 # 隐层神经元个数
BATCH_SIZE = 16 # 一批16个样本
TGT_NET_SYNC = 10 #每隔10轮将参数从原网络同步到目标网络
GAMMA = 0.9 # 折扣率
REPLAY_SIZE = 1000 # 经验回放池容量
LR = 5e-3 # 学习率
EPS_DECAY=0.995 # epsilon因子线性衰减率
# 构建网络
class Net(nn.Module):
def __init__(self, obs_size, hidden_size, n_actions):
# obs_size:输入状态维度,hidden_size:隐层维度,n_actions:输出动作维度
super(Net, self).__init__()
self.net = nn.Sequential(
nn.Linear(obs_size, hidden_size), # 全连接层
nn.ReLU(),
nn.Linear(hidden_size, n_actions) # 全连接层
)
def forward(self, x):
# CartPole is stupid -- they return double observations, rather than standard floats, so, the cast here
return self.net(x.float())
@torch.no_grad() # 下面数据不需要计算梯度,也不会进行反向传播
def unpack_batch(batch, net, gamma):
# batch: 一批次的样本,16个,(state, action, reward, last_state)
states = []
actions = []
rewards = []
done_masks = []
last_states = []
for exp in batch:
states.append(exp.state)
actions.append(exp.action)
rewards.append(exp.reward)
done_masks.append(exp.last_state is None)
if exp.last_state is None:
last_states.append(exp.state)
else:
last_states.append(exp.last_state)
states_v = torch.tensor(states)
actions_v = torch.tensor(actions)
rewards_v = torch.tensor(rewards)
last_states_v = torch.tensor(last_states)
last_state_q_v = net(last_states_v) # 将最后的状态输入网络,得到Q(s, a)
best_last_q_v = torch.max(last_state_q_v, dim=1)[0] # 找最大的Q
best_last_q_v[done_masks] = 0.0
return states_v, actions_v, best_last_q_v * gamma + rewards_v
# r + gamma * max Q(s, a)
if __name__ == "__main__":
env = gym.make("CartPole-v0")
obs_size = env.observation_space.shape[0]
# observation大小(4个状态变量):小车在轨道上的位置,杆子与竖直方向的夹角,小车速度,角度变化率
n_actions = env.action_space.n # action大小(2个动作,左或者右)
net = Net(obs_size, HIDDEN_SIZE, n_actions) # 4->128->2
tgt_net = ptan.agent.TargetNet(net) # 目标网络(与原网络架构一致)
selector = ptan.actions.ArgmaxActionSelector() # 选Q值最大的动作索引
selector = ptan.actions.EpsilonGreedyActionSelector(epsilon=1, selector=selector)
# epsilon-greedy action selector,初始epsilon=1
agent = ptan.agent.DQNAgent(net, selector) # 离散:输出具有最大Q值的动作与状态索引
exp_source = ptan.experience.ExperienceSourceFirstLast(env, agent, gamma=GAMMA)
# 返回运行记录以用于训练模型,输出格式为:(state, action, reward, last_state)
buffer = ptan.experience.ExperienceReplayBuffer(exp_source, buffer_size=REPLAY_SIZE)
# 经验回放池,构建buffer,容量为1000,当前没东西,len(buffer) = 0
optimizer = optim.Adam(net.parameters(), LR) # Adam优化
step = 0 # 迭代次数/轮数
episode = 0 # 局数,几局游戏
solved = False
losses = []
rewards = []
while True:
step += 1
buffer.populate(1) # 从环境中获取一个新样本
for reward, steps in exp_source.pop_rewards_steps():
# pop_rewards_steps(): 返回一局游戏过后的(total_reword,total_steps)
episode += 1
print("第%d次: 第%d局游戏结束, 奖励为%.2f, 本局步数为%d, epsilon为%.2f" %(step, episode, reward, steps, selector.epsilon))
# 杆子能越长时间保持平衡,得分越高。steps与reward一致
rewards.append(reward)
solved = reward > 100 # 最大奖励阈值,只有当reward>100时才结束游戏
if solved:
print("Victory!")
break
# print("第%d次buffer大小:" % step, len(buffer))
if len(buffer) < 2*BATCH_SIZE: # # buffer里面还没超过2倍的批大小(32)个样本
continue
batch = buffer.sample(BATCH_SIZE)
# buffer等于或超过2*BATCH_SIZE后,从buffer里面均匀抽样一个批次的样本,一批BATCH_SIZE个样本
# batch:state, action, reward, last_state
states_v, actions_v, tgt_q_v = unpack_batch(batch, tgt_net.target_model, GAMMA)
# 输入目标网络
# 得到tgt_q_v = r + gamma * max Q(s, a)
optimizer.zero_grad()
q_v = net(states_v) # 输入状态,得到Q(s, a)
q_v = q_v.gather(1, actions_v.unsqueeze(-1)).squeeze(-1)
'''
torch.gather 作用:收集输入的特定维度指定位置的数值
参数:input(tensor): 待操作数。不妨设其维度为(x1, x2, …, xn)
dim(int): 待操作的维度。
index(LongTensor): 如何对input进行操作。
其维度有限定,例如当dim=i时,index的维度为(x1, x2, …y, …,xn),既是将input的第i维的大小更改为y,且要满足y>=1(除了第i维之外的其他维度,大小要和input保持一致)。
out: 注意输出和index的维度是一致的
squeeze(-1): 将输入张量形状中的1去除并返回。
如果输入是形如(A×1×B×1×C×1×D),那么输出形状就为: (A×B×C×D)
'''
loss_v = F.mse_loss(q_v, tgt_q_v)
# MSE Loss, min L = (r + gamma * max Q(s', a') - Q(s, a))^2
loss_v.backward()
optimizer.step()
losses.append(loss_v.item())
selector.epsilon *= EPS_DECAY # 贪心因子线性衰减
if step % TGT_NET_SYNC == 0: # 每TGT_NET_SYNC(10)轮同步一次目标网络参数
tgt_net.sync() # weights from the source network are copied into the target network
# 画图
# Loss曲线图
plt.plot(losses)
plt.xlabel('Iteration', fontsize=13) # 迭代次数
plt.ylabel('Loss', fontsize=13)
plt.title('CartPole-v0', fontsize=14)
plt.savefig('损失函数曲线图.png', dpi=1000)
plt.show()
# reward曲线图
plt.plot(rewards)
plt.xlabel('Episode', fontsize=13) # 几局游戏
plt.ylabel('Reward', fontsize=13)
plt.title('CartPole-v0', fontsize=14)
plt.savefig('奖励曲线图.png', dpi=1000)
plt.show()
6.2 结果
第23次: 第1局游戏结束, 奖励为22.00, 本局步数为22, epsilon为1.00 第47次: 第2局游戏结束, 奖励为24.00, 本局步数为24, epsilon为0.93 第68次: 第3局游戏结束, 奖励为21.00, 本局步数为21, epsilon为0.83 第81次: 第4局游戏结束, 奖励为13.00, 本局步数为13, epsilon为0.78 第109次: 第5局游戏结束, 奖励为28.00, 本局步数为28, epsilon为0.68 第122次: 第6局游戏结束, 奖励为13.00, 本局步数为13, epsilon为0.64 第134次: 第7局游戏结束, 奖励为12.00, 本局步数为12, epsilon为0.60 第165次: 第8局游戏结束, 奖励为31.00, 本局步数为31, epsilon为0.51 第180次: 第9局游戏结束, 奖励为15.00, 本局步数为15, epsilon为0.48 第193次: 第10局游戏结束, 奖励为13.00, 本局步数为13, epsilon为0.45 第204次: 第11局游戏结束, 奖励为11.00, 本局步数为11, epsilon为0.42 第234次: 第12局游戏结束, 奖励为30.00, 本局步数为30, epsilon为0.36 第260次: 第13局游戏结束, 奖励为26.00, 本局步数为26, epsilon为0.32 第302次: 第14局游戏结束, 奖励为42.00, 本局步数为42, epsilon为0.26 第355次: 第15局游戏结束, 奖励为53.00, 本局步数为53, epsilon为0.20 第391次: 第16局游戏结束, 奖励为36.00, 本局步数为36, epsilon为0.17 第402次: 第17局游戏结束, 奖励为11.00, 本局步数为11, epsilon为0.16 第491次: 第18局游戏结束, 奖励为89.00, 本局步数为89, epsilon为0.10 第547次: 第19局游戏结束, 奖励为56.00, 本局步数为56, epsilon为0.08 第681次: 第20局游戏结束, 奖励为134.00, 本局步数为134, epsilon为0.04 Victory!
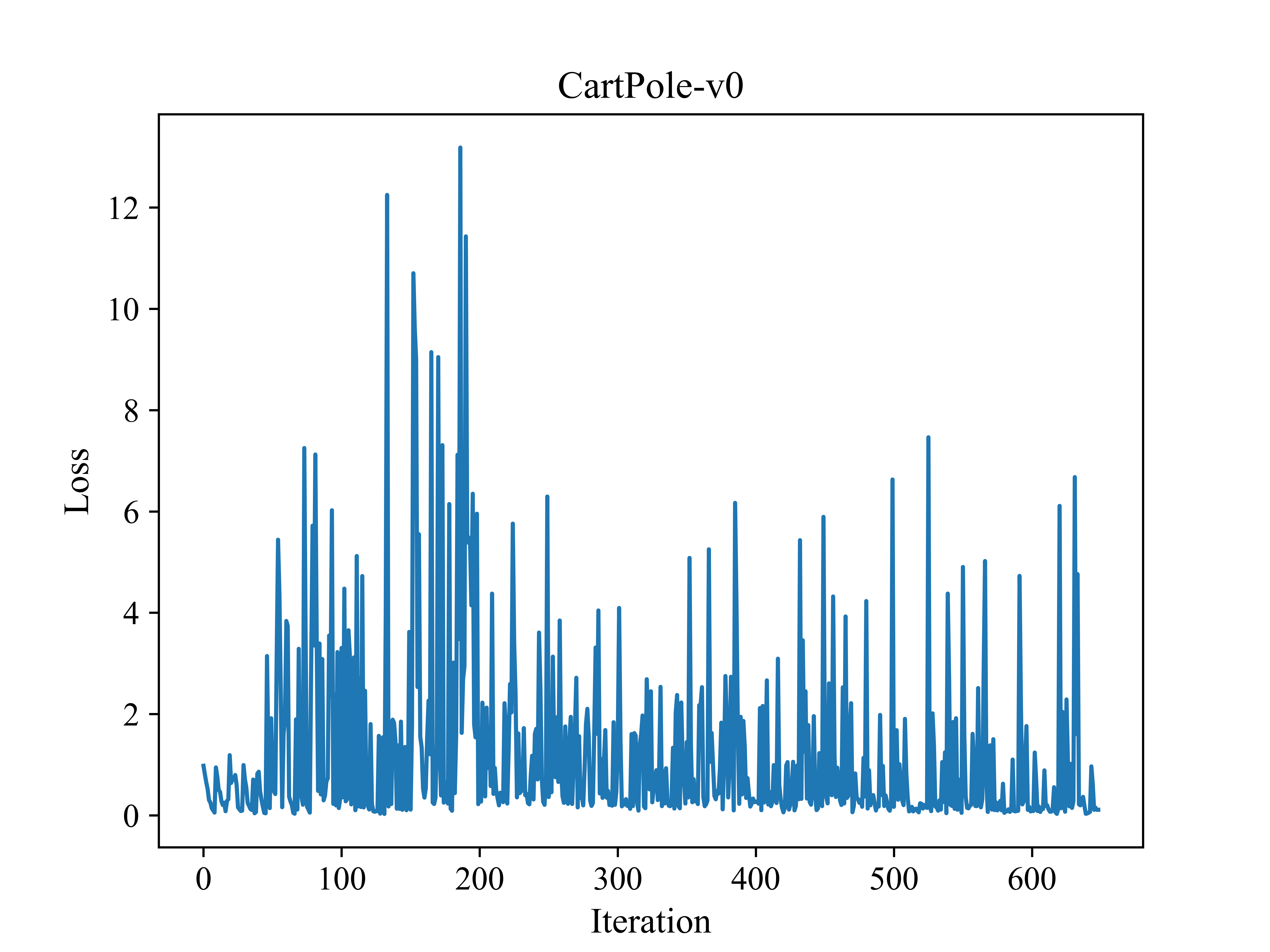
损失函数曲线图
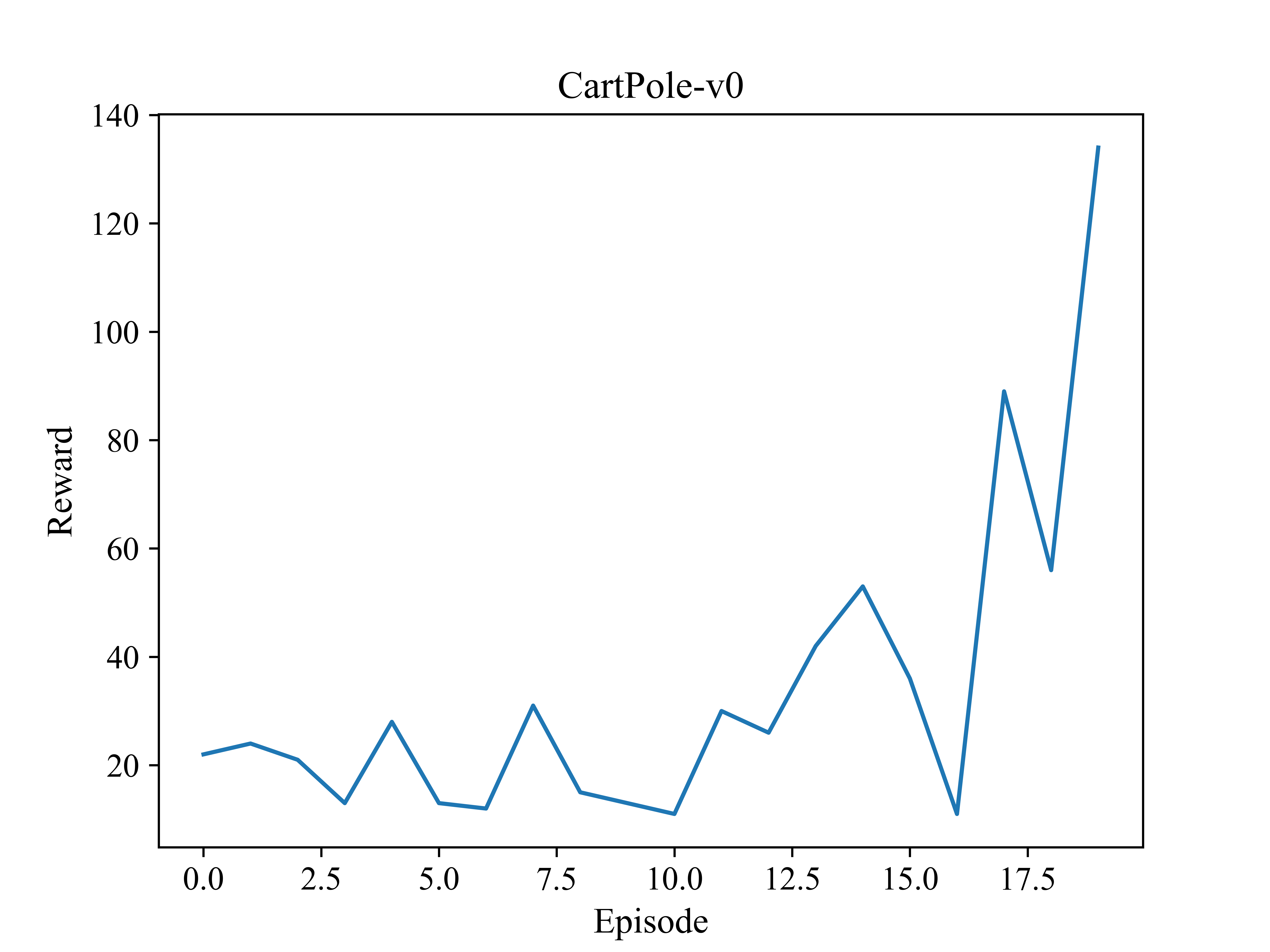
奖励曲线图
7. 参考文献
[1] https://github.com/PacktPublishing/Deep-Reinforcement-Learning-Hands-On-Second-Edition

