Meta-RL——Decoupling Exploration and Exploitation for Meta-Reinforcement Learning without Sacrifices
作者:凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/
这篇博客简要回顾论文“Decoupling Exploration and Exploitation for Meta-Reinforcement Learning without Sacrifices”,并记录一下阅读笔记,论文主要解决的问题是元强化学习中智能体如何学习探索。原先所提出的端到端优化探索与利用方法实现简单,原则上能得到最优策略,但无法摆脱鸡蛋相生问题,一旦探索没学好,利用也就得不到好结果,同时,端到端方式可能会无效探索,浪费了大量的探索来恢复与任务无关的信息,导致学不到最优行为。这篇论文在不牺牲最优性的条件下让探索与利用解耦,从而避免鸡蛋相生问题。
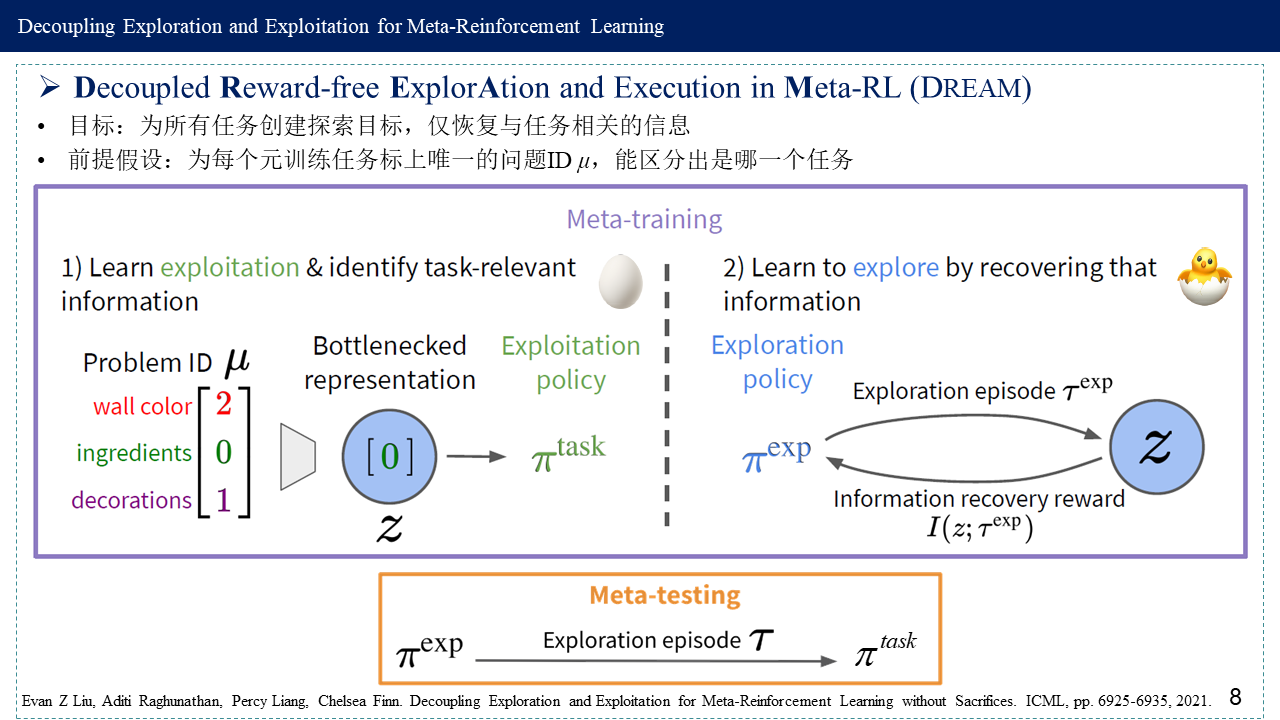
元强化学习(meta-RL)的目标是构建智能体,该智能体能够通过利用相关任务的先前经验快速学习新任务。学习一项新任务通常需要探索以收集与任务相关的信息,并利用这些信息来解决任务。原则上,可以通过简单地最大化任务性能来学习端到端的最佳探索和利用。然而,这种meta-RL方法相当于鸡蛋相生问题,因而可能陷入局部最优解:学习探索需要良好的利用来衡量探索的效用,但学习利用需要通过探索收集信息。分开优化探索和利用的目标可以避免此问题,但先前的meta-RL探索目标会产生收集与任务无关信息的次优策略。论文通过构建一个自动识别任务相关信息的利用目标(最小化信息瓶颈Information Bottleneck)和一个仅恢复该信息的探索目标(最大化互信息)来缓解这两个问题。这避免了端到端训练中的局部最优,而不会牺牲最佳探索。从经验上看,DREAM在复杂的meta-RL问题(如稀疏奖励3D视觉导航)上明显优于现有方法。
1. 基础知识
包括:信息熵(Information Entropy, or Shannon Entropy),联合熵(Joint Entropy)[对称],条件熵(Conditional Entropy)[非对称],互信息(Mutual Information)[对称],相对熵(Relative Entropy, or K-L Divergence)[非对称],互信息与相对熵的关系,信息熵,联合熵,条件熵与互信息的关系,端到端学习(End-to-End Learning),信用/贡献度分配问题(Credit Assignment Problem,CAP),马尔可夫性(无后效性/无记忆性)与非马尔可夫性(Markov vs Non-Markov),鸡蛋相生问题(Chicken-and-Egg Problem),以及探索-利用困境(Exploration-Exploitation Dilemma)。




2. Meta-Reinforcement Learning (元强化学习)


3. End-to-end meta-RL (端到端的元强化学习)及其问题
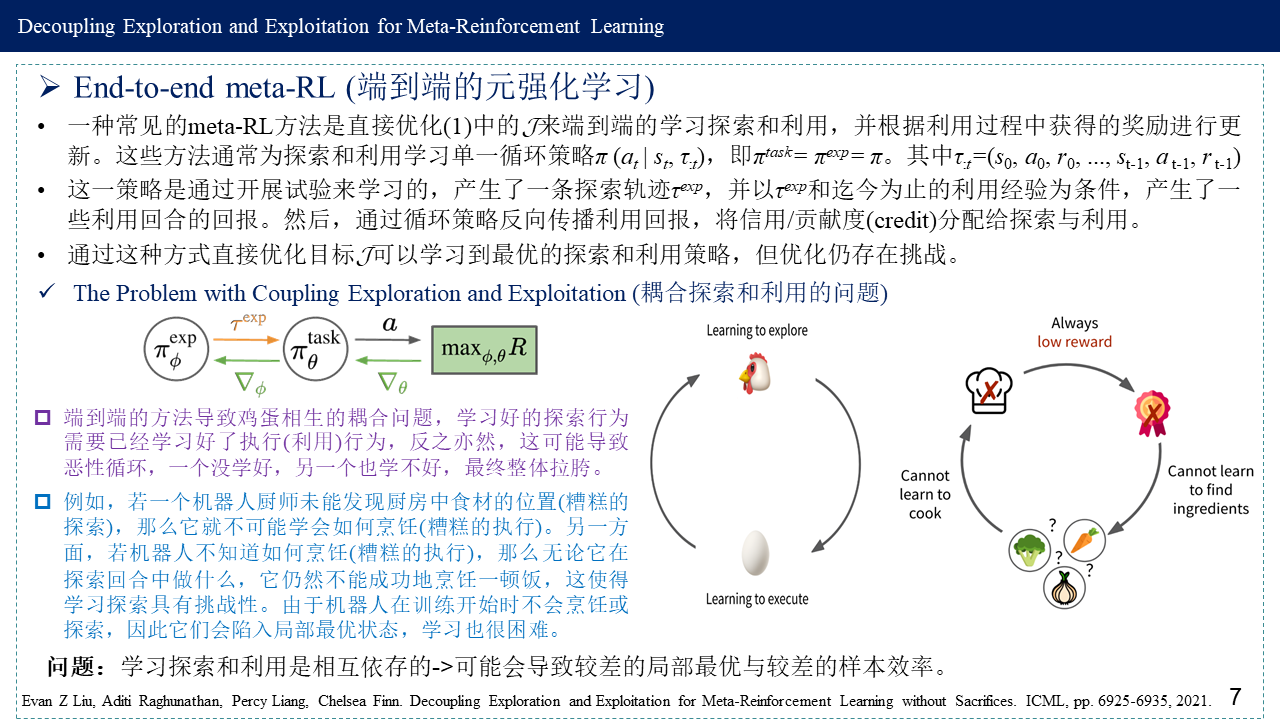
4. Decoupled Reward-free ExplorAtion and Execution in Meta-RL (DREAM)



5. 参考文献
[1] Evan Z Liu, Aditi Raghunathan, Percy Liang, Chelsea Finn. Decoupling Exploration and Exploitation for Meta-Reinforcement Learning without Sacrifices. ICML, pp. 6925-6935, 2021.
Paper: http://proceedings.mlr.press/v139/liu21s.html
Code: https://github.com/ezliu/dream
Slides: https://icml.cc/media/icml-2021/Slides/8991.pdf
Poster: https://docs.google.com/presentation/d/1EsDzcnYghgBNIxGCMbxEdYo6nusgUVC7DpDsusMUshE/edit?usp=sharing
Blog: https://ai.stanford.edu/blog/meta-exploration/
[2] CS330, Meta-RL 2: Learning to explore (Chelsea Finn), https://web.stanford.edu/class/cs330/slides/cs330_metarl2_2021.pdf
[3] Chapter 2: Entropy and Mutual Information https://www.cs.uic.edu/pub/ECE534/WebHome/ch2.pdf
[4] 邱锡鹏,神经网络与深度学习,机械工业出版社,https://nndl.github.io/, 2020.
[5] “Chicken-and-egg.” Dictionary. https://www.learnersdictionary.com/definition/chicken-and-egg. https://idioms.thefreedictionary.com/chicken+and+egg+problem.
[6] 周志华. 机器学习. 清华大学出版社, 2016.
[7] A. A. Alemi, I. Fischer, J. V. Dillon, and K. Murphy. Deep variational information bottleneck. ICLR 2017. https://openreview.net/pdf?id=HyxQzBceg


 浙公网安备 33010602011771号
浙公网安备 33010602011771号