双层优化问题:统一GAN,演员-评论员与元学习方法
(Bilevel Optimization Problem unifies GAN, Actor-Critic, and Meta-Learning Methods)
作者:凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/
之前写过深度学习典型代表——生成对抗网络,写过强化学习典型代表——演员-评论员算法,写过元学习典型代表——MAML算法,现在开始梦幻联动,有没有发现这三个算法有一个共同点,那就是相互博弈(two-player game),两个优化目标交替执行,最终达到某个平衡(纳什均衡),停止迭代。而这个问题在运筹学优化问题中有一个术语,叫做双层优化问题(Bilevel Optimization Problem)。以上三个看似毫无关联的算法最终都归结为双层优化问题,可以用一个公共的表示方法来将这三者统一起来。有了这个结论,这三个看似毫无关联的算法以后优化求解就相当于求解双层优化问题,只要双层优化问题有解决方案,这三者的最优解就能获得。可以使用Kriging逼近来求解双层优化问题[1]。
1. Bilevel Optimization (BLO) Problem

2. Generative Adversarial Networks (GAN)
生成对抗网络(Generative Adversarial Networks, GANs)是通过对抗训练的方式来使得生成网络产生的样本服从真实数据分布在生成对抗网络中,有两个网络进行对抗训练。一个是判别网络,目标是尽量准确地判断一个样本是来自于真实数据还是由生成网络产生;另一个是生成网络,目标是尽量生成判别网络无法区分来源的样本,这两个目标相反的网络不断地进行交替训练当最后收敛时,如果判别网络再也无法判断出一个样本的来源,那么也就等价于生成网络可以生成符合真实数据分布的样本。

3. Actor-Critic (AC) Methods
演员-批评员方法(Actor-Critic, AC)是强化学习中一类长期存在的技术。而大多数强化学习算法要么专注于学习值函数,就像值迭代和时序差分学习一样,要么直接学习策略,就像策略梯度方法一样,AC方法可以同时学习——演员是策略,批评员是值函数。在某些AC方法中,批评员为策略梯度方法提供的方差基线低于从重复值估计的方差基线。在这种情况下,即使对值函数的错误估计也是有用的。因为无论使用何种基线,策略梯度都是无偏的。在其他AC方法中,根据近似值函数更新策略,在这种情况下,可能导致与GANs中类似的病理学。如果针对错误的值函数对策略进行优化,则可能会导致错误的策略,该策略永远不会充分探索空间,从而阻止找到好的值函数,并导致退化解。

补充:生成对抗网络 vs 演员-评论员
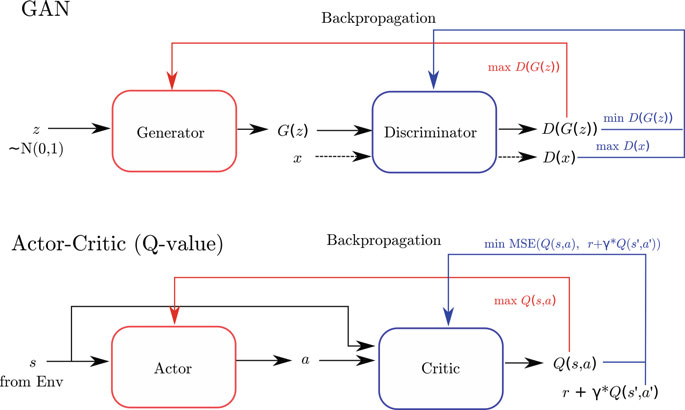
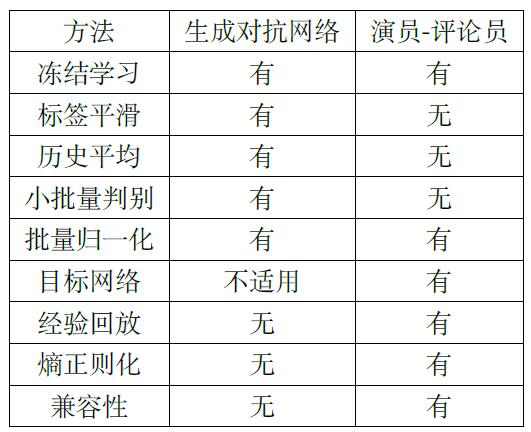
4. Meta-Learning
元学习(Meta Learning)通常可以理解为学会学习(Learn to Learn);在多个学习事件中改进学习算法的过程。相比之下,传统的机器学习改进了对一组数据样本的模型预测。在基础学习过程中,内部(或下层/基础)学习算法解决了由数据集和目标定义的任务,如图像分类。在元学习过程中,外部(或上层/元)算法更新内部学习算法,使其学习的模型改进外部目标。例如,这个目标可能是泛化性能或内部算法的学习速度。

补充(与上述关系不太大,仅供自己学习参考):从三个角度解释元强化学习,即RNN, 双层优化,以及推断问题。
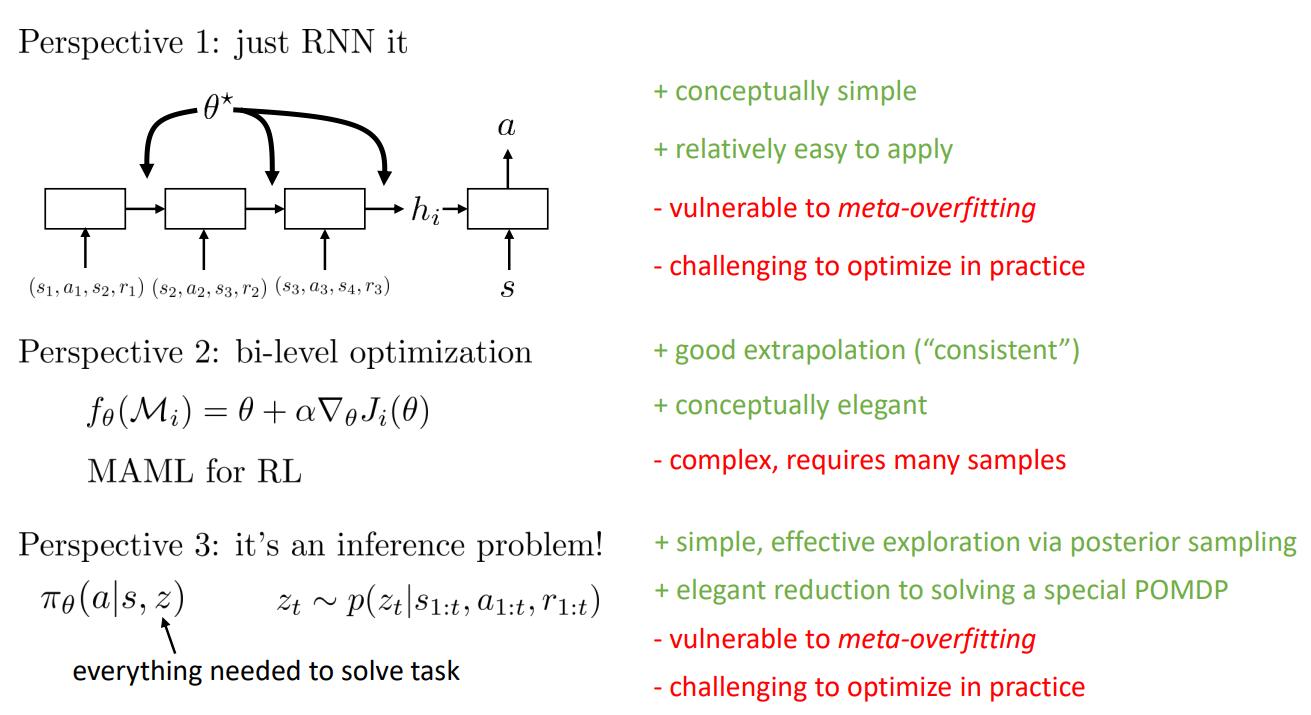
学习,元学习,强化学习,元强化学习四种方法总结:

图源:CS 285 Meta-Learning 2020 http://rail.eecs.berkeley.edu/deeprlcourse-fa20/static/slides/lec-22.pdf
5. 参考文献
[1] A. Sinha and V. Shaikh, "Solving Bilevel Optimization Problems Using Kriging Approximations," IEEE Transactions on Cybernetics, doi: 10.1109/TCYB.2021.3061551.
[2] David Pfau, Oriol Vinyals, “Connecting Generative Adversarial Networks and Actor-Critic Methods”, arXiv preprint, 2016.
[3] T. M. Hospedales, A. Antoniou, P. Micaelli and A. J. Storkey, "Meta-Learning in Neural Networks: A Survey," IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021.

