浅谈范数正则化 - 凯鲁嘎吉

作者：凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/

这篇博客介绍不同范数作为正则化项时的作用。首先介绍了常见的向量范数与矩阵范数，然后说明添加正则化项的原因，之后介绍向量的$L_0$，$L_1$，$L_2$范数及其作为正则化项的作用，对三者进行比较分析，并用贝叶斯观点解释传统线性模型与正则化项。随后，介绍矩阵的$L_{2, 1}$范数及其推广形式$L_{p, q}$范数，以及矩阵的核范数及其推广形式Schatten范数。最后，用MATLAB程序编写了Laplace分布与Gauss分布的概率密度函数图。有关矩阵范数优化求解问题可参考：一类涉及矩阵范数的优化问题 - 凯鲁嘎吉 - 博客园

1. 向量范数与矩阵范数

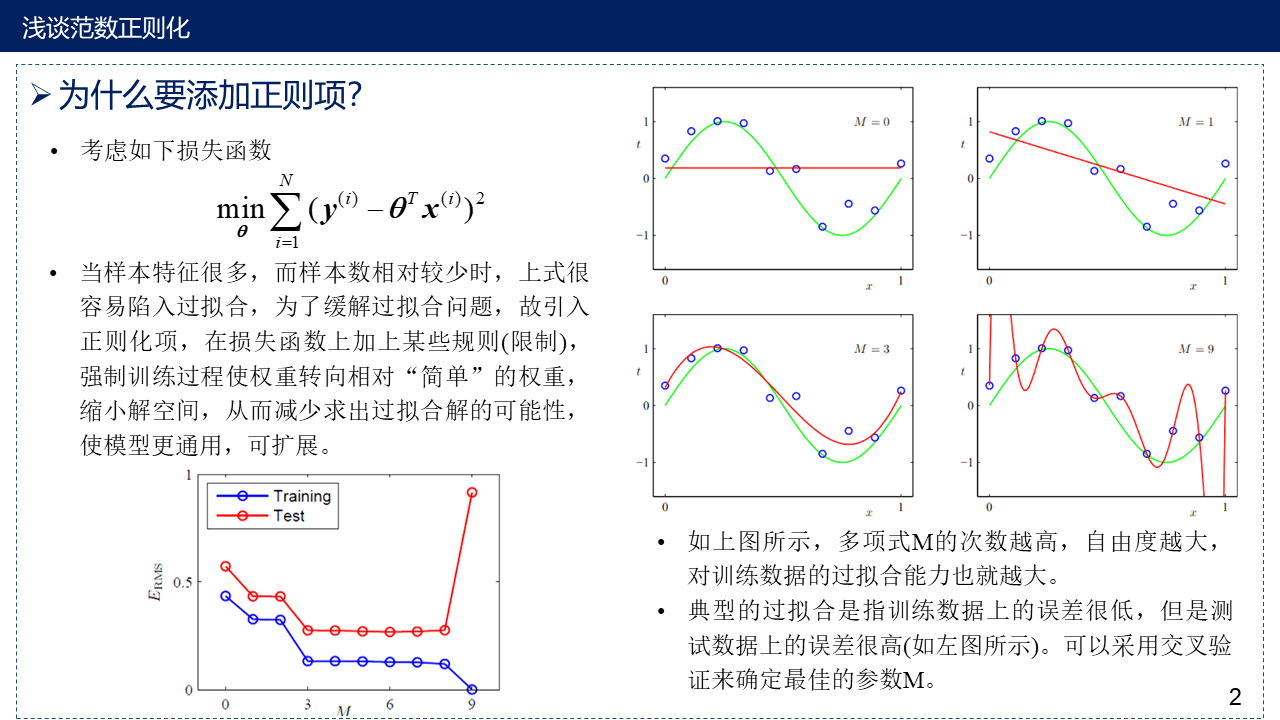
2. 为什么要添加正则项？

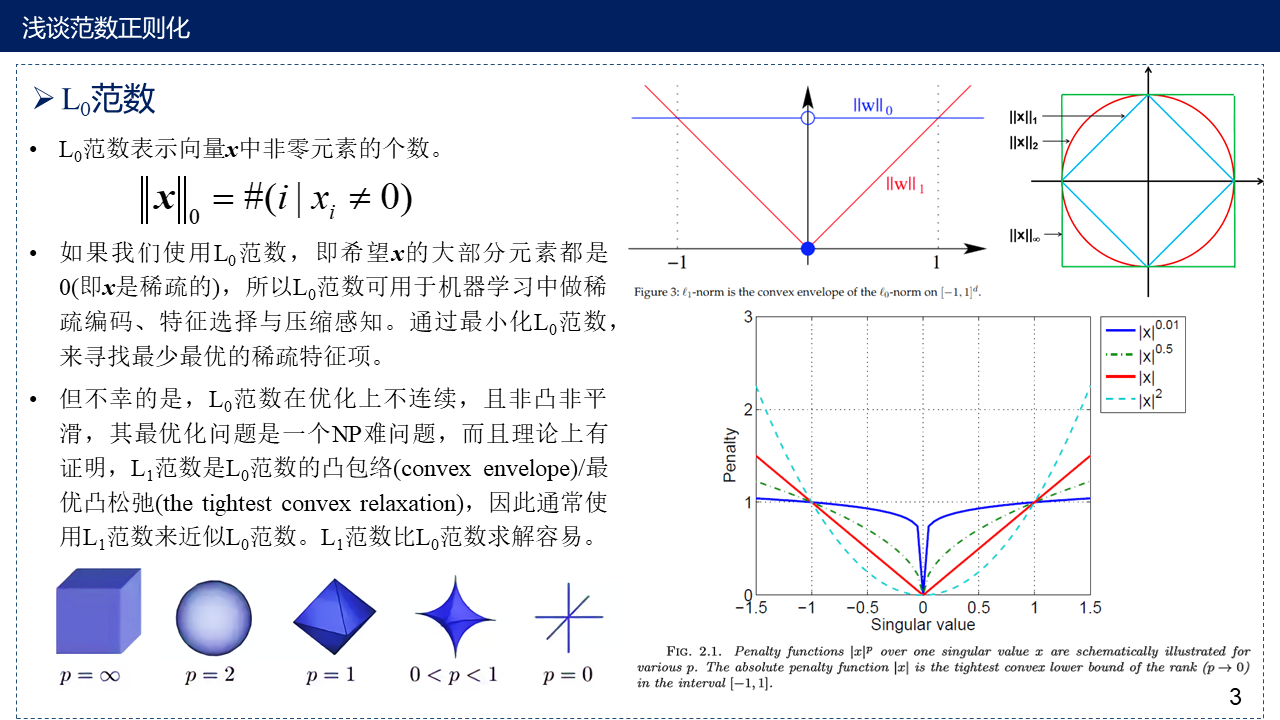
3. $L_0$范数

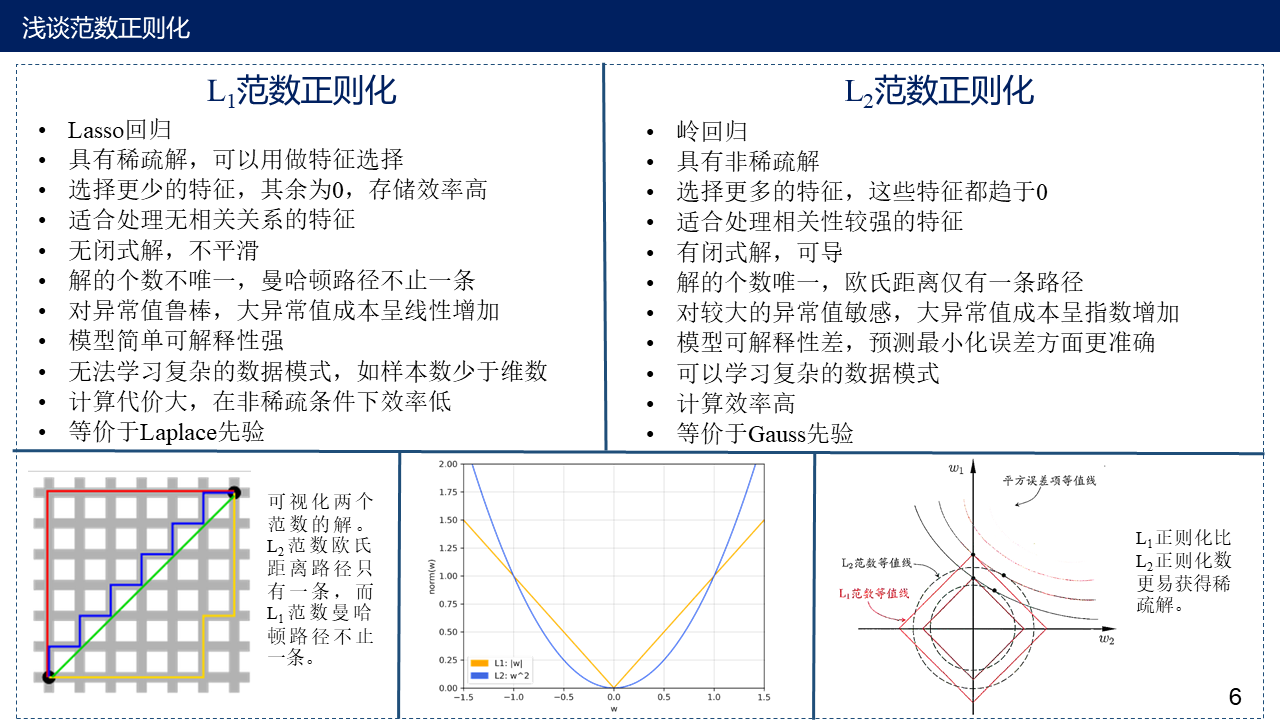
4. $L_1$范数

5. $L_2$范数

6. $L_1$范数与$L_2$范数作为正则项的区别

7. 用概率解释传统线性回归模型

8. $L_2$范等价于Gauss先验

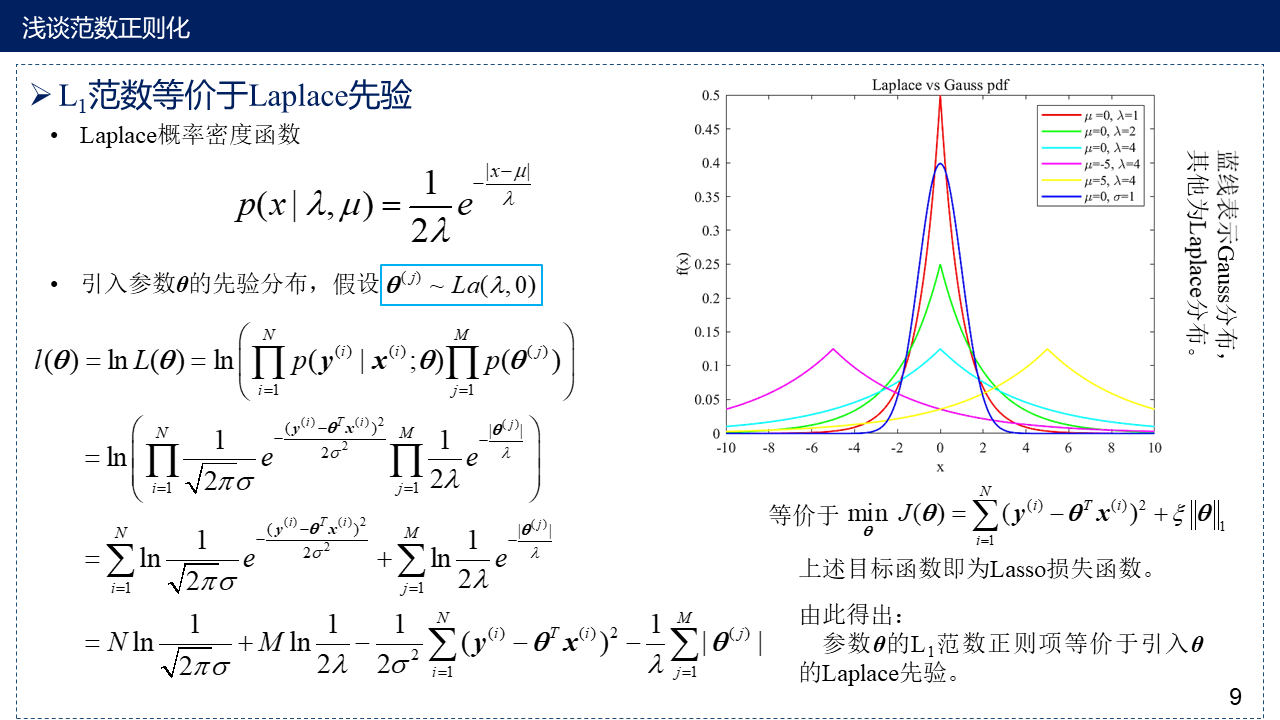
9. $L_1$范数等价于Laplace先验

10. 矩阵的$L_{2, 1}$范数及$L_{p, q}$范数

11. 矩阵的核范数及Schatten范数

12. MATLAB程序：Laplace分布与Gauss分布的概率密度函数图

%% Demo of Laplace Density Function
% x : variable
% lambda : size para
%miu: location para
clear
clc
x = -10:0.1:10;
y_1=Laplace_distribution(x, 0, 1);
y_2=Laplace_distribution(x, 0, 2);
y_3=Laplace_distribution(x, 0, 4);
y_4=Laplace_distribution(x, -5, 4);
y_5=Laplace_distribution(x, 5, 4);
y_6=normpdf(x,0,1);
plot(x, y_1, 'r-', x, y_2, 'g-', x, y_3, 'c-', x, y_4, 'm-', x, y_5, 'y-', x, y_6, 'b-', 'LineWidth',1.2);
legend('\mu =0, \lambda=1','\mu=0, \lambda=2','\mu=0, \lambda=4','\mu=-5, \lambda=4','\mu=5, \lambda=4', '\mu=0, \sigma=1'); %图例的设置
xlabel('x');
ylabel('f(x)');
title('Laplace vs Gauss pdf');
set(gca, 'FontName', 'Times New Roman', 'FontSize',11);
saveas(gcf,sprintf('demo_Laplace_Gauss.jpg'),'bmp'); %保存图片

%% Laplace Density Function
function y=Laplace_distribution(x, miu, lambda)
    y = 1 / (2*lambda) * exp( -abs(x-miu)/lambda);
end