一类涉及矩阵范数的优化问题
作者:凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/
这篇博文主要探讨一下有关矩阵范数的优化问题,我们知道,矩阵按行或列拆开就是向量,因此矩阵范数优化问题在某种程度上可以转化为向量范数的优化,而向量拆开是一个个数值,因此向量优化问题就进一步退化为单变量优化。因此,我们从最基础的单变量优化出发,单变量优化问题搞清楚之后,再逐步拓展到向量、矩阵范数的优化上。文中涉及到向量范数、矩阵范数、软阈值算子(soft thresholding/shrinkage operator)与奇异值收缩算子(singular value shrinkage operator)等概念。这类优化问题在矩阵补全/填充、压缩感知、稀疏表达、低秩矩阵分解(比如张长青2015在ICCV会议上发表的Low-Rank Tensor Constrained Multiview Subspace Clustering中E与G的求解问题)、鲁棒主成分分析(Robust PCA)等领域有广泛的应用。尤其是矩阵的$L_{2,1}$范数与矩阵的核范数/迹范数(nuclear/trace norm)在去噪去冗余降维等方面应用最广。
1. 向量范数与矩阵范数

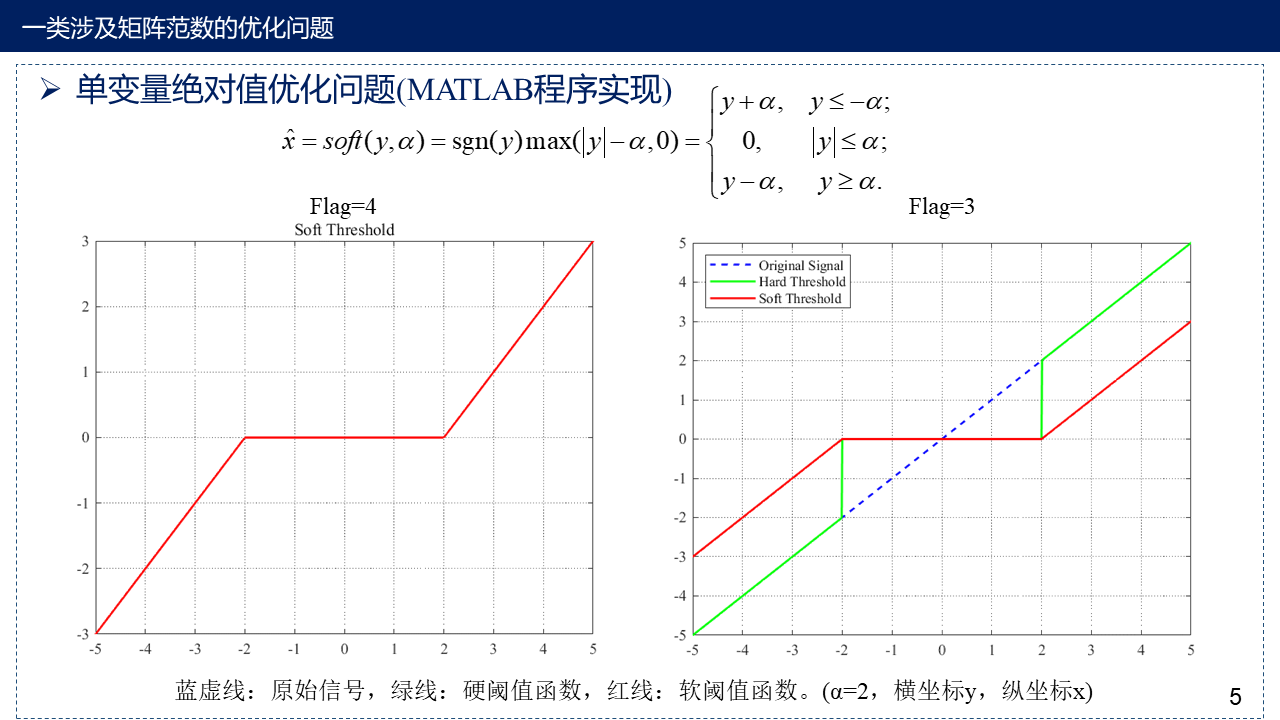
2. 单变量绝对值优化问题



3. 向量范数优化问题

4. 矩阵$L_{2,1}$范数优化问题

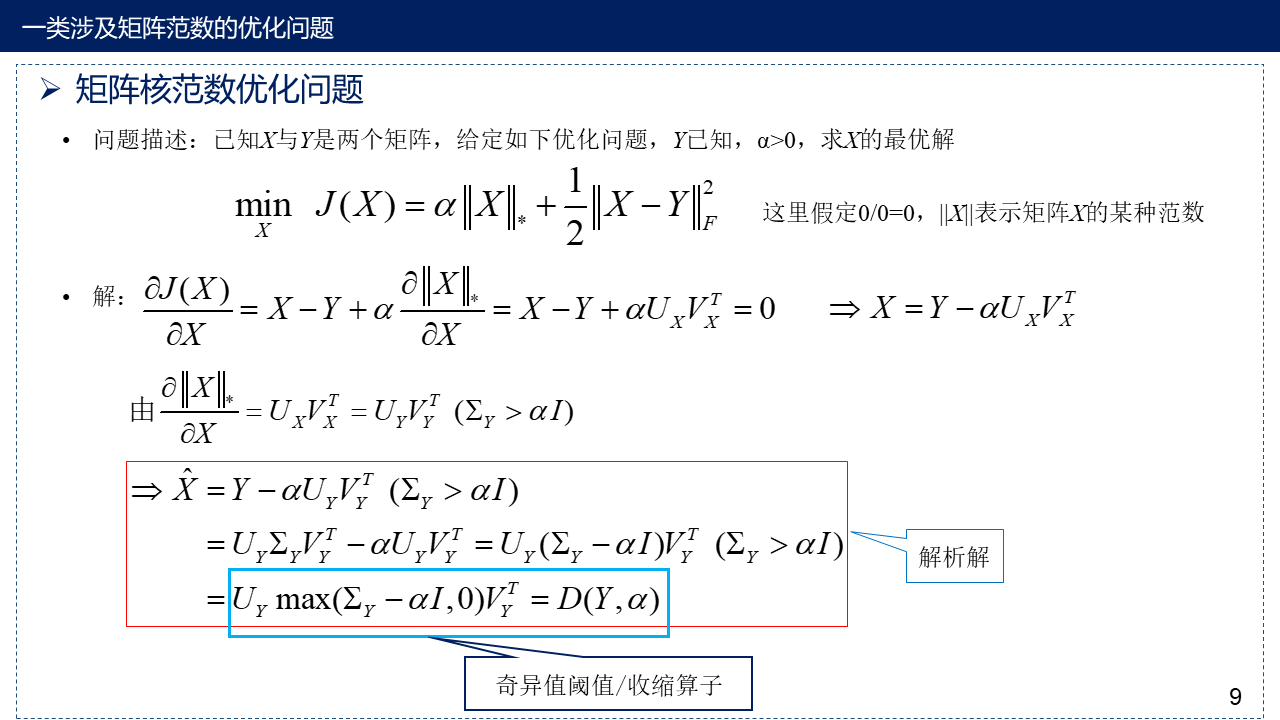
5. 矩阵核范数优化问题

6. MATLAB程序
这个程序主要集中于单变量绝对值优化与向量的2范数优化问题。flag=1是向量的优化,其中我们用两种方法进行求解,解析解与数值解,从结果可以看出,在数值解拥有足够的迭代次数时,两者结果大体一致。flag=2是单变量绝对值优化问题,可以直观看出变量x与最优值之间的函数图像。flag=3与flag=4是软阈值函数图像,结果见PPT第5页。
clear
clc
flag=2; % flag=1, 向量; flag=2, 单变量(一个数值); flag=3, MATLAB自带的软阈值函数; flag=4, 自定义软阈值函数
%% 向量的情况 2D shrinkage formula
% 最小化问题:z(x)=alpha*||x||+(beta/2)*||x-y||^2
% alpha=0.5;
% beta=1;
% 用的2范数
if flag==1
% 法1:解析解
% 当||y||>alpha,x=(||y||-alpha/beta).*(y/||y||)
y=0.1:0.1:1;
num=length(y);
yy=norm(y, 2);
x_1=((yy-0.5)/yy).*y;
z_1=0.5*norm(x_1, 2)+0.5.*(x_1-y)*(x_1-y)';
% 法2:数值解--只要重复次数够大,能逼近解析解的结果
% x=(||y||/((alpha/beta)+||y||)).*y
N=50; %重复迭代N次
x_2=rand(1, num);
for i=1:N
xx=norm(x_2, 2);
x_2=(xx/(0.5+xx)).*y;
end
z_2=0.5*norm(x_2, 2)+0.5.*(x_2-y)*(x_2-y)';
% 结果
x_result=[x_1; x_2] % x的结果, 第一行是方法1的结果, 第二行是方法2的结果
z=[z_1; z_2] % 最小化问题z的结果, 第一行是方法1的结果, 第二行是方法2的结果
%% 单变量的情况 1D shrinkage formula
elseif flag==2
% z(x)=(beta/2)*(x-y)^2+alpha*|x|
% alpha=0.5, beta=1
% 当|y|>alpha, x=(|y|-alpha)*(y/|y|)
x=0.1:0.1:1;
y=1;
z=0.5.*(x-y).^2+0.5.*abs(x);
[z_min, index]=min(z);
plot(x, z);
hold on
plot(x(index), z_min, 'ro');
xlabel('x');
ylabel('z');
x_result=x(index)
z=z_min
%% MATLAB自带的软阈值函数 1D shrinkage formula
elseif flag==3
x=-5:0.01:5;
thr=2;
% z(x)=(beta/2)*(x-y)^2+alpha*|x|
% thr=alpha/beta
ysoft=wthresh(x,'s',thr); % 软阈值
ythard = wthresh(x,'h',thr); % 硬阈值
plot(x, x, 'b--', x, ythard, 'g-', x, ysoft, 'r-', 'LineWidth',1.3);
legend('Original Signal','Hard Threshold','Soft Threshold', 'Location', 'northwest'); %图例的设置
% 设置网格线
grid on;
set(gca, 'FontName','Times New Roman');
set(gca, 'GridLineStyle', ':');
set(gca, 'GridAlpha', 1);
saveas(gcf,sprintf('matlab_shrinkage.jpg'),'bmp'); %保存图片
%% 自定义软阈值函数 1D shrinkage formula
elseif flag==4
x=-5:0.01:5;
thr=2;
y=Soft_Threshold(x,thr);
plot(x, y, 'r-', 'LineWidth',1.3)
title('Soft Threshold');
% 设置网格线
grid on;
set(gca, 'FontName','Times New Roman');
set(gca, 'GridLineStyle', ':');
set(gca, 'GridAlpha', 1);
saveas(gcf,sprintf('soft_shrinkage.jpg'),'bmp'); %保存图片
end
% 自定义软阈值函数
% z(x)=(beta/2)*(x-y)^2+alpha*|x|
% thr=alpha/beta
function y=Soft_Threshold(x,thr)
y=sign(x).*max(abs(x) - thr,0);
end
当flag=1时,给出向量最优化问题,x_result与z的第一行是解析解的结果,第二行是数值解的结果,可以看到在一定精度范围内两者结果一致。(前提是数值解需要一定的迭代次数)
x_result =
0.0745 0.1490 0.2236 0.2981 0.3726 0.4471 0.5216 0.5961 0.6707 0.7452
0.0745 0.1490 0.2236 0.2981 0.3726 0.4471 0.5216 0.5961 0.6707 0.7452
z =
0.8561
0.8561
当flag=2时,可以从图中看出变量x与目标函数之间的曲线图。
x_result =
0.5000
z =
0.3750

7. 参考文献
[1] Yang, Junfeng & Yin, Wotao & Zhang, Yin & Wang, Yilun. (2009). A Fast Algorithm for Edge-Preserving Variational Multichannel Image Restoration. SIAM J. Imaging Sciences. 2. 569-592.
[2] Liu, Jun & Ji, Shuiwang & Ye, Jieping. (2009). Multi-Task Feature Learning Via Efficient l2, 1-Norm Minimization. Proceedings of the 25th Conference on Uncertainty in Artificial Intelligence, UAI 2009. 339-348.
[3] Peng, Yali & Sehdev, Paramjit & Liu, Shigang & Li, Jun & Wang, Xili. (2018). l2,1-norm minimization based negative label relaxation linear regression for feature selection. Pattern Recognition Letters. 116.
[4] Cai, Jian-Feng & Candès, Emmanuel & Shen, Zuowei. (2010). A Singular Value Thresholding Algorithm for Matrix Completion. SIAM Journal on Optimization. 20. 1956-1982.
[5] 最优化之Robust PCA - 博客园 - quarryman
[6] linear algebra - Derivative of the nuclear norm - Mathematics Stack Exchange
[7] 2010 Proximal gradient method (PPT)
[8] Toh, Kim-Chuan & Yun, Sangwoon. (2010). An Accelerated Proximal Gradient Algorithm for Nuclear Norm Regularized Least Squares Problems. Pacific Journal of Optimization. 6.
[9] ECE236C - Optimization Methods for Large-Scale Systems http://www.seas.ucla.edu/~vandenbe/ee236c.html
[10] 潘少华, 文再文. 低秩稀疏矩阵优化问题的模型与算法[J]. 运筹学学报, 2020(3):1-26.

