关于“Unsupervised Deep Embedding for Clustering Analysis”的优化问题
作者:凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/
Deep Embedding Clustering (DEC)和Improved Ceep Emdedding Clustering (IDEC)被相继提出,但关于参数的优化问题,作者并未详细给出,于是乎自己推导了一遍,但是发现关于聚类中心的偏导和这两篇文章的推导结果不一致,不知道问题出在哪?下面,相当于给出一道数学题,来求解目标函数关于某个参数的偏导问题。
2023.4.10 更新:原文推导见评论一楼,原文没错,我错了,i与j不应该混为一谈。类似的求导:https://peterroelants.github.io/posts/cross-entropy-softmax/#Derivative-of-the-cross-entropy-loss-function-for-the-softmax-function
问题描述
已知
\[L=\sum\limits_{i}^{N}{\sum\limits_{j}^{c}{{{p}_{ij}}\log \frac{{{p}_{ij}}}{{{q}_{ij}}}}}\]
\[{{q}_{ij}}=\frac{{{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-1}}}{\sum\nolimits_{j}{{{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-1}}}}\]
\[{{p}_{ij}}=\frac{q_{ij}^{2}/\sum\nolimits_{i}{{{q}_{ij}}}}{\sum\nolimits_{j}{(q_{ij}^{2}/\sum\nolimits_{i}{{{q}_{ij}}})}}\]
固定${p}_{ij}$, 求$\frac{\partial L}{\partial {{z}_{i}}}$, $\frac{\partial L}{\partial {{\mu }_{j}}}$
问题求解
1. 先求$\frac{\partial L}{\partial {{z}_{i}}}$
根据链式法则
\[\frac{\partial L}{\partial {{z}_{i}}}=\sum\limits_{j}^{c}{\frac{\partial L}{\partial {{q}_{ij}}}\frac{\partial {{q}_{ij}}}{\partial {{z}_{i}}}}\]
\[\frac{\partial L}{\partial {{q}_{ij}}}=\frac{\partial \left( {{p}_{ij}}\log \frac{{{p}_{ij}}}{{{q}_{ij}}} \right)}{\partial {{q}_{ij}}}=\frac{\partial \left( {{p}_{ij}}\log {{p}_{ij}}-{{p}_{ij}}\log {{q}_{ij}} \right)}{\partial {{q}_{ij}}}=-\frac{{{p}_{ij}}}{{{q}_{ij}}}\]
\[ \frac{\partial {{q}_{ij}}}{\partial {{z}_{i}}}=\frac{-2{{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-2}}({{z}_{i}}-{{\mu }_{j}})\sum\limits_{l}^{c}{{{(1+{{\left\| {{z}_{i}}-{{\mu }_{l}} \right\|}^{2}})}^{-1}}}-{{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-1}}\cdot (-2)\cdot \sum\limits_{l}^{c}{{{(1+{{\left\| {{z}_{i}}-{{\mu }_{l}} \right\|}^{2}})}^{-2}}({{z}_{i}}-{{\mu }_{l}})}}{{{\left( \sum\limits_{l}^{c}{{{(1+{{\left\| {{z}_{i}}-{{\mu }_{l}} \right\|}^{2}})}^{-1}}} \right)}^{2}}} \\ =-2{{q}_{ij}}({{z}_{i}}-{{\mu }_{j}}){{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-1}}+2{{q}_{ij}}\frac{\sum\limits_{l}^{c}{{{(1+{{\left\| {{z}_{i}}-{{\mu }_{l}} \right\|}^{2}})}^{-2}}({{z}_{i}}-{{\mu }_{l}})}}{\sum\limits_{l}^{c}{{{(1+{{\left\| {{z}_{i}}-{{\mu }_{l}} \right\|}^{2}})}^{-1}}}} \]
其中用到${{\left( \frac{A}{B} \right)}^{\prime }}=\frac{{{A}^{\prime }}B-A{{B}^{\prime }}}{{{B}^{2}}}$,以及上下同乘以$q_{ij}$.
因此,
\[\frac{\partial L}{\partial {{z}_{i}}}=\sum\limits_{j}^{c}{\frac{\partial L}{\partial {{q}_{ij}}}\frac{\partial {{q}_{ij}}}{\partial {{z}_{i}}}}\\ =\sum\limits_{j}^{c}{-\frac{{{p}_{ij}}}{{{q}_{ij}}}\left( -2{{q}_{ij}}({{z}_{i}}-{{\mu }_{j}}){{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-1}}+2{{q}_{ij}}\frac{\sum\limits_{l}^{c}{{{(1+{{\left\| {{z}_{i}}-{{\mu }_{l}} \right\|}^{2}})}^{-2}}({{z}_{i}}-{{\mu }_{l}})}}{\sum\limits_{l}^{c}{{{(1+{{\left\| {{z}_{i}}-{{\mu }_{l}} \right\|}^{2}})}^{-1}}}} \right)}\\ =\sum\limits_{j}^{c}{2{{p}_{ij}}({{z}_{i}}-{{\mu }_{j}}){{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-1}}}-\sum\limits_{j}^{c}{2{{p}_{ij}}\frac{\sum\limits_{l}^{c}{{{(1+{{\left\| {{z}_{i}}-{{\mu }_{l}} \right\|}^{2}})}^{-2}}({{z}_{i}}-{{\mu }_{l}})}}{\sum\limits_{l}^{c}{{{(1+{{\left\| {{z}_{i}}-{{\mu }_{l}} \right\|}^{2}})}^{-1}}}}}\\ =\sum\limits_{j}^{c}{2{{p}_{ij}}({{z}_{i}}-{{\mu }_{j}}){{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-1}}}-2\frac{\sum\limits_{l}^{c}{{{(1+{{\left\| {{z}_{i}}-{{\mu }_{l}} \right\|}^{2}})}^{-2}}({{z}_{i}}-{{\mu }_{l}})}}{\sum\limits_{l}^{c}{{{(1+{{\left\| {{z}_{i}}-{{\mu }_{l}} \right\|}^{2}})}^{-1}}}}\\ =\sum\limits_{j}^{c}{2{{p}_{ij}}({{z}_{i}}-{{\mu }_{j}}){{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-1}}}-2\frac{\sum\limits_{j}^{c}{{{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-2}}({{z}_{i}}-{{\mu }_{j}})}}{\sum\limits_{l}^{c}{{{(1+{{\left\| {{z}_{i}}-{{\mu }_{l}} \right\|}^{2}})}^{-1}}}}\\ =\sum\limits_{j}^{c}{2{{p}_{ij}}({{z}_{i}}-{{\mu }_{j}}){{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-1}}}-2\frac{\sum\limits_{j}^{c}{{{q}_{ij}}{{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-2}}({{z}_{i}}-{{\mu }_{j}})}}{{{q}_{ij}}\sum\limits_{l}^{c}{{{(1+{{\left\| {{z}_{i}}-{{\mu }_{l}} \right\|}^{2}})}^{-1}}}}\\ =\sum\limits_{j}^{c}{2{{p}_{ij}}({{z}_{i}}-{{\mu }_{j}}){{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-1}}}-2\frac{\sum\limits_{j}^{c}{{{q}_{ij}}{{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-2}}({{z}_{i}}-{{\mu }_{j}})}}{{{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-1}}}\\ =\sum\limits_{j}^{c}{2{{p}_{ij}}({{z}_{i}}-{{\mu }_{j}}){{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-1}}}-2\sum\limits_{j}^{c}{{{q}_{ij}}{{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-1}}({{z}_{i}}-{{\mu }_{j}})}\\ =\sum\limits_{j}^{c}{2({{p}_{ij}}-{{q}_{ij}})({{z}_{i}}-{{\mu }_{j}}){{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-1}}} \]
其中用到$\sum\limits_{j}^{c}{{{p}_{ij}}}=1$.
2. 再求$\frac{\partial L}{\partial {{\mu }_{j}}}$
根据链式法则
\[\frac{\partial L}{\partial {{\mu }_{j}}}=\sum\limits_{i}^{N}{\frac{\partial L}{\partial {{q}_{ij}}}\frac{\partial {{q}_{ij}}}{\partial {{\mu }_{j}}}}\]
\[\frac{\partial {{q}_{ij}}}{\partial {{\mu }_{j}}}=\frac{2{{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-2}}({{z}_{i}}-{{\mu }_{j}})\sum\limits_{l}^{c}{{{(1+{{\left\| {{z}_{i}}-{{\mu }_{l}} \right\|}^{2}})}^{-1}}}-{{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-1}}\cdot 2{{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-2}}({{z}_{i}}-{{\mu }_{j}})}{{{\left( \sum\limits_{l}^{c}{{{(1+{{\left\| {{z}_{i}}-{{\mu }_{l}} \right\|}^{2}})}^{-1}}} \right)}^{2}}}\\ =2({{z}_{i}}-{{\mu }_{j}}){{q}_{ij}}{{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-1}}-2q_{ij}^{2}{{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-1}}({{z}_{i}}-{{\mu }_{j}})\\ =2{{q}_{ij}}(1-{{q}_{ij}})({{z}_{i}}-{{\mu }_{j}}){{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-1}} \]
因此,
\[\frac{\partial L}{\partial {{\mu }_{j}}}=\sum\limits_{i}^{N}{\frac{\partial L}{\partial {{q}_{ij}}}\frac{\partial {{q}_{ij}}}{\partial {{\mu }_{j}}}}=\sum\limits_{i}^{N}{\left( -\frac{{{p}_{ij}}}{{{q}_{ij}}}\cdot 2{{q}_{ij}}(1-{{q}_{ij}})({{z}_{i}}-{{\mu }_{j}}){{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-1}} \right)}=\sum\limits_{i}^{N}{\left( 2{{p}_{ij}}({{q}_{ij}}-1)({{z}_{i}}-{{\mu }_{j}}){{(1+{{\left\| {{z}_{i}}-{{\mu }_{j}} \right\|}^{2}})}^{-1}} \right)}\]
原文结果
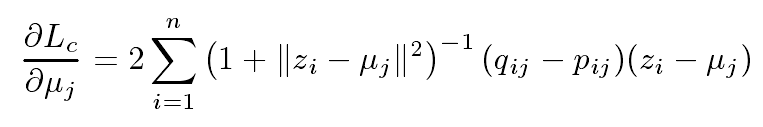
不知道问题出在哪?虽然这些推导结果并不影响最终的实验结果,毕竟直接调用函数就可以出来,不需要亲自动手推,但是我觉得原文给出的这个结果可能不对,求广大网友指正~
参考文献
[1] Deep Clustering Algorithms - 凯鲁嘎吉 博客园
[2] Xie J, Girshick R, Farhadi A. Unsupervised deep embedding for clustering analysis[C]//International conference on machine learning. 2016: 478-487.
[3] Guo X, Gao L, Liu X, et al. Improved deep embedded clustering with local structure preservation[C]//IJCAI. 2017: 1753-1759.

