MATLAB实例：BP神经网络用于回归任务

阅读目录(Content)

• MATLAB实例：BP神经网络用于回归(非线性拟合)任务
• 问题描述
• MATLAB程序
• BP_kailugaji.m
• demo.m
• 结果

回到顶部(go to top)

MATLAB实例：BP神经网络用于回归(非线性拟合)任务

作者：凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/

问题描述

    给定多元(多维)数据X，有真实结果Y，对这些数据进行拟合(回归)，得到拟合函数的参数，进而得到拟合函数，现在进来一些新样本，对这些新样本进行预测出相应地Y值。通常的最小二乘法进行线性拟合并不适用于所有数据，对于大多数数据而言，他们的拟合函数是非线性的，人为构造拟合函数相当困难，没有一定的经验积累很难完美的构造出符合条件的拟合函数。因此神经网络在这里被应用来做回归(拟合)任务，进一步用来预测。神经网络是很强大的拟合工具，虽然数学可解释性差，但拟合效果好，因而得到广泛应用。BP神经网络是最基础的网络结构，输入层，隐层，输出层，三层结构。如下图所示。

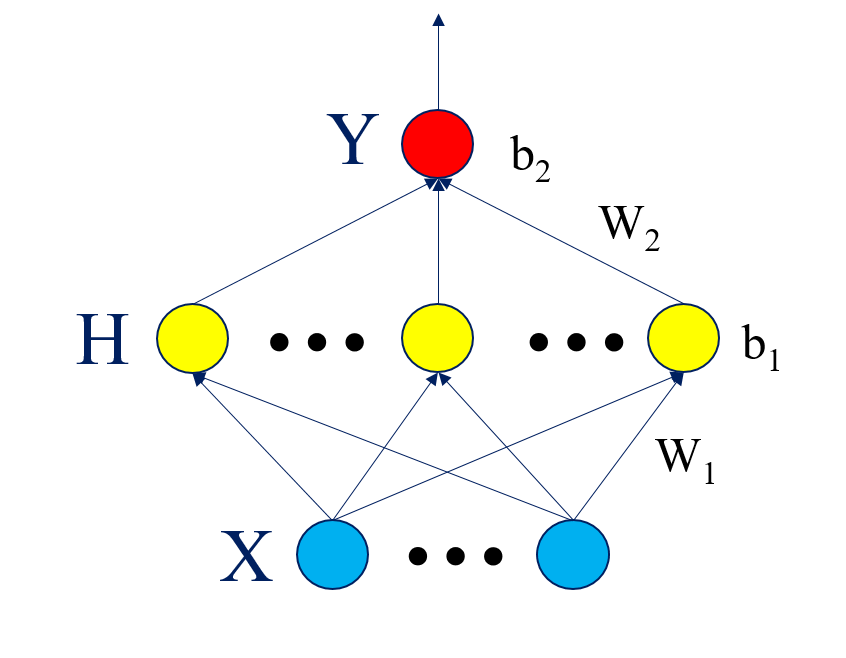
整体的目标函数就是均方误差

$L=||f(X)-Y||_{2}^{2}$

其中(激活函数可以自行设定)

$f(X)=purelin\left( {{W}_{2}}\cdot \tan sig({{W}_{1}}\cdot X+{{b}_{1}})+{{b}_{2}} \right)$

$N$: 输入数据的个数

$D$: 输入数据的维度

${{D}_{1}}$: 隐层节点的个数

$X$: 输入数据($D$*$N$)

$Y$: 真实输出(1*$N$)

${{W}_{1}}$: 输入层到隐层的权值(${{D}_{1}}$*$D$)

${{b}_{1}}$: 隐层的偏置(${{D}_{1}}$*1)

${{W}_{2}}$: 输入层到隐层的权值(1*${{D}_{1}}$)

${{b}_{2}}$: 隐层的偏置(1*1)

通过给定训练数据与训练标签来训练网络的权值与偏置，进一步得到拟合函数$f(X)$。这样，来了新数据后，直接将新数据X代入函数$f(X)$，即可得到预测的结果。

y = tansig(x) = 2/(1+exp(-2*x))-1；
y = purelin(x) = x；

MATLAB程序

用到的数据为UCI数据库的housing数据：https://archive.ics.uci.edu/ml/machine-learning-databases/housing/

输入数据，最后一列是真实的输出结果，将数据打乱顺序，95%的作为训练集，剩下的作为测试集。这里隐层节点数为20。

BP_kailugaji.m

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69

function errorsum=BP_kailugaji(data_load, NodeNum, ratio) % Author：凯鲁嘎吉 https://www.cnblogs.com/kailugaji/ % Input: % data_load: 最后一列真实输出结果 % NodeNum: 隐层节点个数 % ratio: 训练集占总体样本的比率 [Num, ~]=size(data_load); data=data_load(:, 1:end-1); real_label=data_load(:, end);    k=rand(1,Num); [~,n]=sort(k); kk=floor(Num*ratio);    %找出训练数据和预测数据 input_train=data(n(1:kk),:)'; output_train=real_label(n(1:kk))'; input_test=data(n(kk+1:Num),:)'; output_test=real_label(n(kk+1:Num))';    %选连样本输入输出数据归一化 [inputn,inputps]=mapminmax(input_train); [outputn,outputps]=mapminmax(output_train);    %% BP网络训练 % %初始化网络结构 net=newff(inputn, outputn, NodeNum);    net.trainParam.epochs=100; % 最大迭代次数 net.trainParam.lr=0.01;  % 步长 net.trainParam.goal=1e-5;  % 迭代终止条件 % net.divideFcn = '';    %网络训练 net=train(net,inputn,outputn);    W1=net.iw{1, 1}; b1=net.b{1}; W2=net.lw{2, 1}; b2=net.b{2}; fun1=net.layers{1}.transferFcn; fun2=net.layers{2}.transferFcn;    %% BP网络预测 %预测数据归一化 inputn_test=mapminmax('apply',input_test,inputps);     %网络预测输出 an=sim(net,inputn_test);     %网络输出反归一化 BPoutput=mapminmax('reverse',an,outputps);      %% 结果分析 figure(1) plot(BPoutput,'-.or') hold on plot(output_test,'-*b'); legend('预测输出','期望输出') xlim([1 (Num-kk)]); title('BP网络预测输出','fontsize',12) ylabel('函数输出','fontsize',12) xlabel('样本','fontsize',12) saveas(gcf,sprintf('BP网络预测输出.jpg'),'bmp'); %预测误差 error=BPoutput-output_test; errorsum=sum(mse(error)); % 保留参数 save BP_parameter W1 b1 W2 b2 fun1 fun2 net inputps outputps

demo.m

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

clear;clc;close all data_load=dlmread('housing.data'); NodeNum=20; ratio=0.95; errorsum=BP_kailugaji(data_load, NodeNum, ratio); fprintf('测试集总体均方误差为：%f\n', errorsum);   %% % 验证原来的或者预测新的数据 num=1; % 验证第num行数据 load('BP_parameter.mat'); data=data_load(:, 1:end-1); real_label=data_load(:, end); X=data(num, :); X=X'; Y=real_label(num, :); %% BP网络预测 %预测数据归一化 X=mapminmax('apply',X,inputps); %网络预测输出 Y_pre=sim(net,X); %网络输出反归一化 Y_pre=mapminmax('reverse',Y_pre,outputps);   error=Y_pre-Y'; errorsum=sum(mse(error)); fprintf('第%d行数据的均方误差为：%f\n', num, errorsum);

结果

?

1 2	测试集总体均方误差为：5.184424 第1行数据的均方误差为：3.258243

注意：隐层节点个数，激活函数，迭代终止条件等等参数需要根据具体数据进行调整。