MATLAB小函数：计算Metropolis-Hastings Weights

MATLAB小函数：计算Metropolis-Hastings Weights 

作者：凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/

问题：已经得到一个无向连通图，知道各个节点之间的连接情况，求节点之间的Metropolis-Hastings权重。

前提：用MATLAB实例：构造网络连接图(Network Connection)及计算图的代数连通度(Algebraic Connectivity)中的函数构造得到网络连接图，并得到Network.mat。

1. 网络连接图

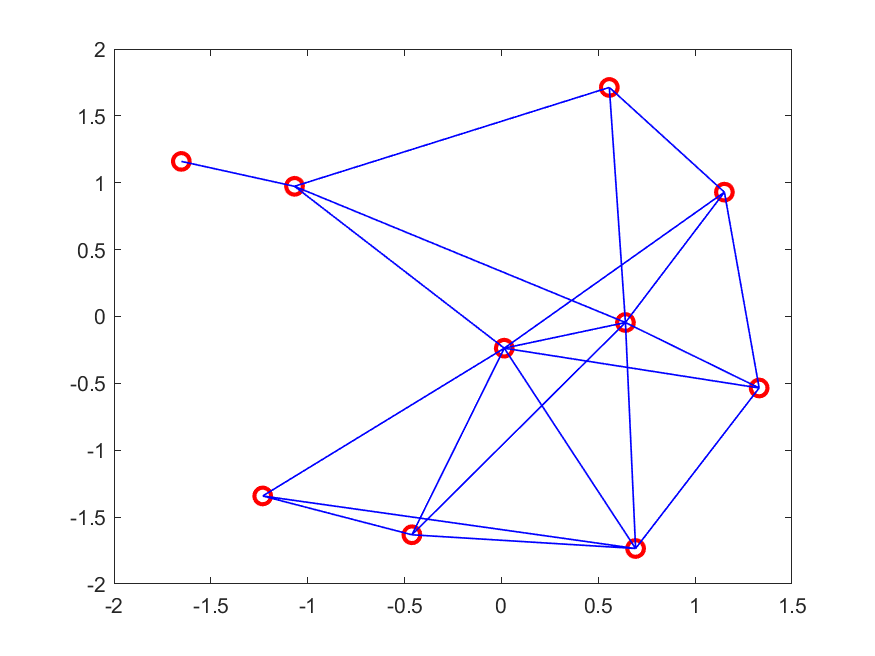
网络连接情况如下：

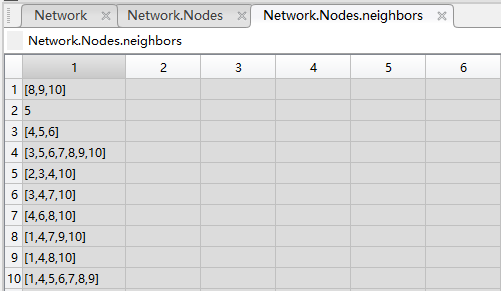
2. Metropolis-Hastings Weights

3. Metropolis_Weights.m

function W = Metropolis_Weights(Network)
% Author: kailugaji
% 凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/
NodeNum= Network.Conf.NodeNumber; %节点个数
W=zeros(NodeNum, NodeNum);
s=0;
for i=1:NodeNum
    K=length(Network.Nodes.neighbors{i});
    % i=j
    for k=1:K
        index=Network.Nodes.neighbors{i}(k);
        s=s+1./(max(K,length(Network.Nodes.neighbors{index}))+1);
    end
    W(i, i)=1-s;
    s=0;
    % i~=j
    for j=1:NodeNum
        if (sum(Network.Nodes.neighbors{i}==j)==1) && (i~=j)
            W(i, j)=1./(max(K,length(Network.Nodes.neighbors{j}))+1);
        elseif (sum(Network.Nodes.neighbors{i}==j)==0) && (i~=j)
            W(i, j)=0;
        end
    end
end         

4. 结果

>> load('Network_1.mat')
>> format short
>> W = Metropolis_Weights(Network)

W =

    0.5083         0         0         0         0         0         0    0.1667    0.2000    0.1250
         0    0.8000         0         0    0.2000         0         0         0         0         0
         0         0    0.4750    0.1250    0.2000    0.2000         0         0         0         0
         0         0    0.1250    0.1250    0.1250    0.1250    0.1250    0.1250    0.1250    0.1250
         0    0.2000    0.2000    0.1250    0.3500         0         0         0         0    0.1250
         0         0    0.2000    0.1250         0    0.3500    0.2000         0         0    0.1250
         0         0         0    0.1250         0    0.2000    0.3833    0.1667         0    0.1250
    0.1667         0         0    0.1250         0         0    0.1667    0.2500    0.1667    0.1250
    0.2000         0         0    0.1250         0         0         0    0.1667    0.3833    0.1250
    0.1250         0         0    0.1250    0.1250    0.1250    0.1250    0.1250    0.1250    0.1250

拓展：实际上得到的Metropolis-Hastings权重是一个对称双随机矩阵，即：

双随机矩阵（doubly stochastic matrix）：元素属于[0,1]，行和为1，且列和为1。

参考：

[1] 构造n阶对称双随机矩阵MATLAB实例：对称双随机矩阵

[2] 几种双随机权重矩阵的设计：S. Silva Pereira, “Distributed consensus algorithms for wireless sensor networks: convergence analysis and optimization,” Tesi doctoral, UPC, Departament de Teoria del Senyal i Comunicacions, 2012.中的3.4.1节： Review of Common Weight Matrix Designs