基于图嵌入的高斯混合变分自编码器的深度聚类
Deep Clustering by Gaussian Mixture Variational Autoencoders with Graph Embedding, DGG
作者:凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/
1. 引言
这篇博文主要是对论文“Deep Clustering by Gaussian Mixture Variational Autoencoders with Graph Embedding”的整理总结,这篇文章将图嵌入与概率深度高斯混合模型相结合,使网络学习到符合全局模型和局部结构约束的强大特征表示。将样本作为图上的节点,并最小化它们的后验分布之间的加权距离,在这里使用Jenson-Shannon散度作为距离度量。
阅读这篇博文的前提条件是:了解高斯混合模型用于聚类的算法,了解变分推断与变分自编码器,进一步了解变分深度嵌入(VaDE)模型。在知道高斯混合模型(GMM)与变分自编码器(VAE)之后,VaDE实际上是将这两者结合起来的一个产物。与VAE相比,VaDE在公式推导中多了一个变量c。与GMM相比,变量c就相当于是GMM中的隐变量z,而隐层得到的特征z相当于原来GMM中的数据x。而基于图嵌入的高斯混合变分自编码器的深度聚类(DGG)模型可以看做在VAE的基础上结合了高斯混合模型与图嵌入来完成聚类过程,公式推导中同样增加了表示类别的变量c,同时,目标函数后面加了一项图嵌入的约束项。比起VaDE来说,可以理解为多了一个约束项——图嵌入,当然目标函数还是有所不同。
下面主要介绍DGG模型目标函数的数学推导过程。推导过程用到了概率论与数理统计的相关知识,更用到了VaDE模型推导里面的知识,如果想要深入了解推导过程,请先看变分深度嵌入(VaDE)模型的“前提公式”。
2. 目标函数的由来与转化






3. 目标函数具体推导


用Siamese网络来度量数据点之间的相似度,从而选出数据点xi的邻居。


其中,D是数据x的维度,M是隐层z的维度,K是聚类数。



第二项和第四项最后一步怎么来的?用到了一个公式,公式的具体推导见:变分深度嵌入(VaDE)模型的“前提公式”。
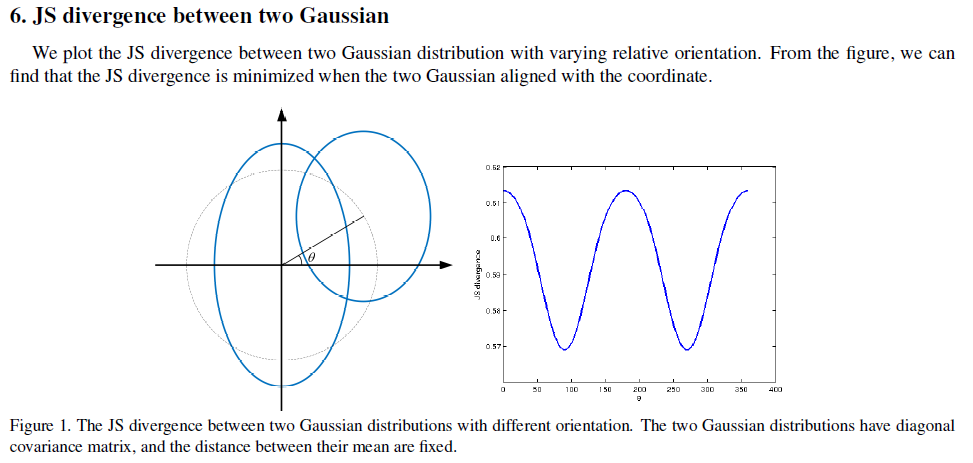
4. 参数更新过程及聚类结果

我也搞不明白哪个图正确,或者都不正确,望指正。
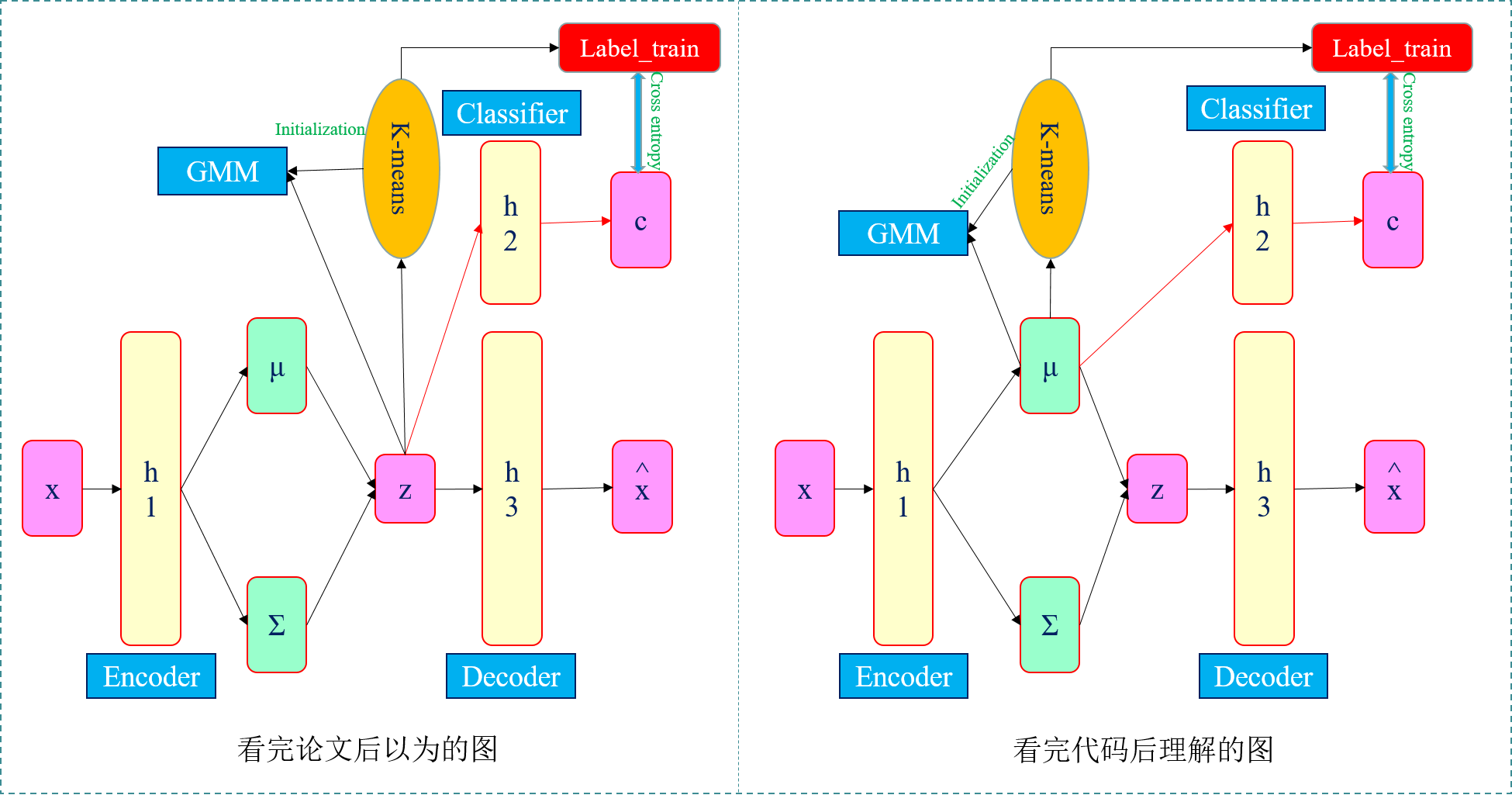
5. 我的思考
- 在推导过程中我与原文中的推导有不一样的地方。
1)我的推导过程中变分下界L中第二项系数是1/2,原文直接是1,而在支撑材料里面仍然是1/2,因此可以认为是作者笔误造成的。
2)我的推导过程中变分下界L中的第二项与第四项都有常数项(蓝框框标出的),这两项正好正负抵消,才没有这个常数项,而在原文支撑材料里面直接第二四项都没有常数项。不过这只是支撑材料的内容,在原文中没有太大影响。


-
这里有一点和VaDE不一样,VaDE聚类结果是由${{\gamma }_{ik}}$后验概率通过贝叶斯公式得到的,中间过程并没有参与梯度下降的更新,而DGG这里是构建了一个分类器网络f2,从而得到聚类结果。
1)DGG这里有三个网络,f1是编码器,g是解码器,而f2是分类器。
2)这种架构和苏剑林博客中提到的VAE用于聚类的算法"变分自编码器(四):一步到位的聚类方案 - 科学空间|Scientific Spaces"的网络架构有异曲同工之妙,不过苏剑林博客中的网路框架还多了一个自定义的Gaussian层,有兴趣的可以看看苏剑林那篇文章及代码。
-
原文中分类器的输入应该是VAE模型得到的隐层z,而代码里面是VAE得到的x_mean,没有经过采样得到z,直接用x_mean作为分类器的输入,这一点不知道是我理解有误,还是代码问题。
- 关于预训练:首先训练DAE作为VAE的初始化,训练VAE得到隐层参数${\mu}_{i}$,用K-means对${\mu}_{i}$进行聚类,得到聚类中心作为GMM的初始类均值,K-means得到类标签,计算样本方差作为GMM初始类协方差矩阵。分类器部分用SGD进行微调,将${{\gamma }_{ik}}$作为分类器输出,并用${{\gamma }_{ik}}$得到的聚类结果与K-means得到的初始标签之间的交叉熵作为分类器的损失函数,从而预训练分类器的参数。
- 关于Siamese网络找邻居:通过神经网络训练得到10维的隐层特征,对隐层计算相似性,代码中是用Siamese网络找到数据点的前100个邻居,但后来又从这100个邻居中随机取20个作为数据点的20个邻居,为什么不是先对100个邻居排序,取最近的前20个?或许我代码理解问题,求指教。
-
关于邻居:预训练阶段自己算自己的,不涉及邻居。正式训练时,代码中将自己本身的数据与20个邻居的数据放在一起,形成一个三维矩阵,第一维代表样本个数,第二维代表数据的维度,第三维代表自己+邻居的ID。例如:image_train[:,:,0]代表数据本身,image_train[:,:,1]代表数据的第一个邻居。这样将数据本身与邻居整合在一起,整体作为输入数据,送进网络进行训练。这种设计相当巧妙,相当于以空间换时间,减少训练过程中用来查找邻居的时间。同时,DGG总体损失函数$\underset{\phi ,\theta }{\mathop{\max }}\,\frac{1}{2}\sum\limits_{i=1}^{N}{\sum\limits_{j=1}^{N}{{{w}_{ij}}(L(\theta ,\phi ;{{x}_{i}})+L(\theta ,\phi ;{{x}_{i}},{{x}_{j}}))}}$可以将这两项合并成一项,既计算了自己与自己的损失函数,也计算了自己与邻居的损失函数。
-
关于${{\pi }_{ik}}$:这篇文章中参数${{\pi }_{ik}}$与GMM中的混合比例不太一样,计算${{\pi }_{ik}}$时是通过拉格朗日乘数法进行求解的${{\pi }_{ik}}=\frac{\sum\limits_{j\in {{\Omega }_{i}}}{{{w}_{ij}}{{\gamma }_{ik}}}}{\sum\limits_{j\in {{\Omega }_{i}}}{{{w}_{ij}}\left( {{\gamma }_{ik}}+{{\gamma }_{jk}} \right)}}$,但在代码中定义的${{\pi }_{ik}}$的更新公式与原文提到的更新公式不一致。

-
同时,在定义GMM类的时候,计算后验概率${{\gamma }_{ik}}$时并没有出现混合比例${{\pi }_{k}}$,没有用GMM中${{\gamma }_{ik}}$的更新公式${{\gamma }_{ik}}=\frac{{{\pi }_{k}}N({{x}_{i}}|{{\mu }_{k}},{{\Sigma }_{k}})}{\sum\limits_{k=1}^{K}{{{\pi }_{k}}N({{x}_{i}}|{{\mu }_{k}},{{\Sigma }_{k}})}}$进行计算。

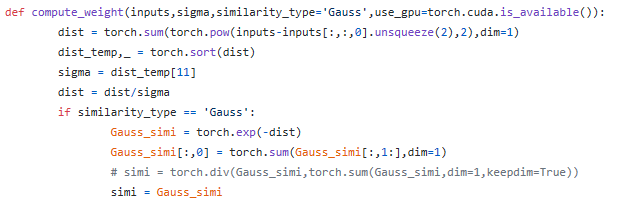
- 代码中计算相似度矩阵${w}_{ij}$时,窗口大小sigma的选取有歧义,函数中已经有了输入变量sigma,但是里面又重新定义了sigma=dist_temp[11],这样的话输入sigma还有什么意义?无论输入多少都无所谓,因为会被新定义的覆盖掉。同时,sigma为什么要这样定义?为什么是[11]?
-
DGG原作者给的代码里面说预训练的参数是从VaDE代码里面获得的。这里VaDE与DGG在训练同一组数据用的VAE网络架构是一致的,因此可以直接拿来用。如果数据是新的,首先需要训练Siamese网络来找数据点的邻居,然后自己构建深度自编码器或者变分自编码器预训练模型参数。
6. 参考文献
[1] Linxiao Yang, Ngai-Man Cheung, Jiaying Li, and Jun Fang, "Deep Clustering by Gaussian Mixture Variational Autoencoders with Graph Embedding", In ICCV 2019.
[2] 论文补充材料:Deep Clustering by Gaussian Mixture Variational Autoencoders with Graph Embedding - Supplementary
[3] DGG Python代码:https://github.com/ngoc-nguyen-0/DGG
[4] 变分深度嵌入(Variational Deep Embedding, VaDE) - 凯鲁嘎吉 - 博客园
[5] 变分推断与变分自编码器 - 凯鲁嘎吉 - 博客园



