变分深度嵌入(Variational Deep Embedding, VaDE)
作者:凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/
这篇博文主要是对论文“Variational Deep Embedding: An Unsupervised and Generative Approach to Clustering”的整理总结,阅读这篇博文的前提条件是:了解高斯混合模型用于聚类的算法,了解变分推断与变分自编码器。在知道高斯混合模型(GMM)与变分自编码器(VAE)之后,VaDE实际上是将这两者结合起来的一个产物。与VAE相比,VaDE在公式推导中多了一个变量c。与GMM相比,变量c就相当于是GMM中的隐变量z,而隐层得到的特征z相当于原来GMM中的数据x。下面主要介绍VaDE模型的变分下界(损失函数)L(x)的数学推导过程。推导过程用到了概率论与数理统计的相关知识。
1. 前提公式

计算过程中用到了正态分布的一阶矩与二阶矩计算公式。
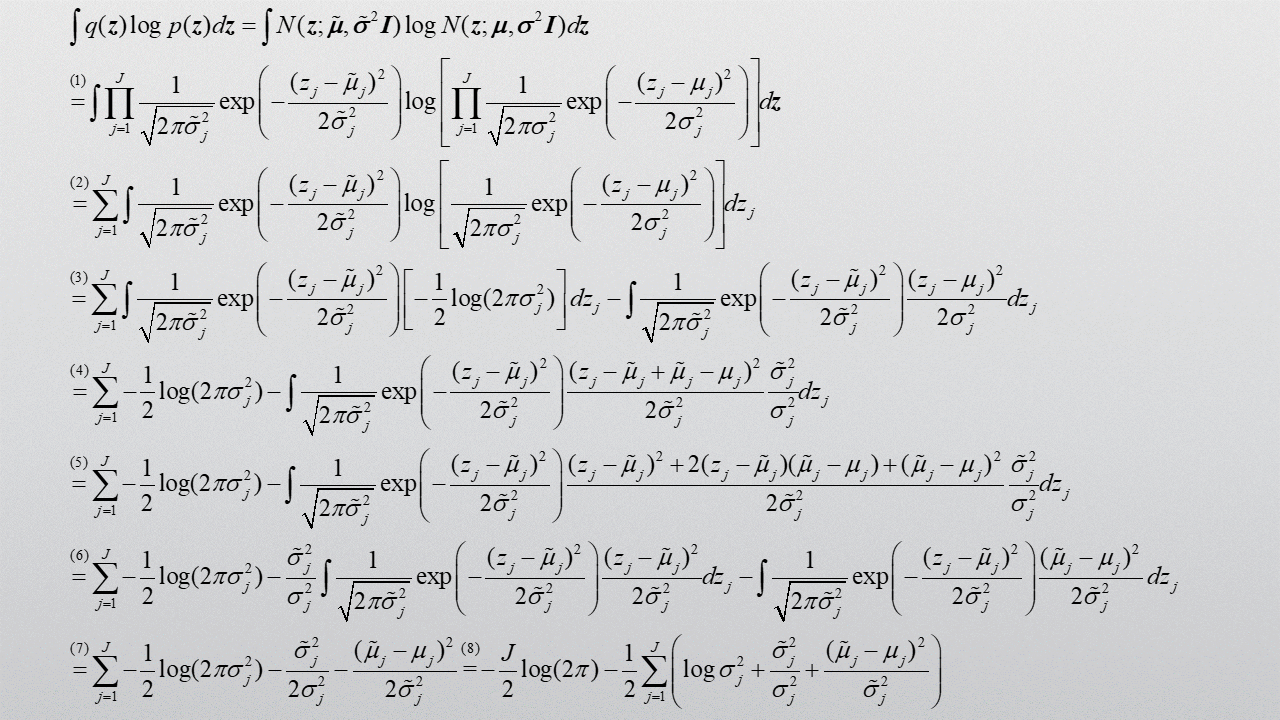

2. VaDE损失函数公式推导过程


最终的聚类结果是由q(c|x)得到的,q(c|x)相当于GMM中的隐变量的后验概率γ。

下面将损失函数拆成5项,并一项一项进行求解。






3. VaDE算法总体流程
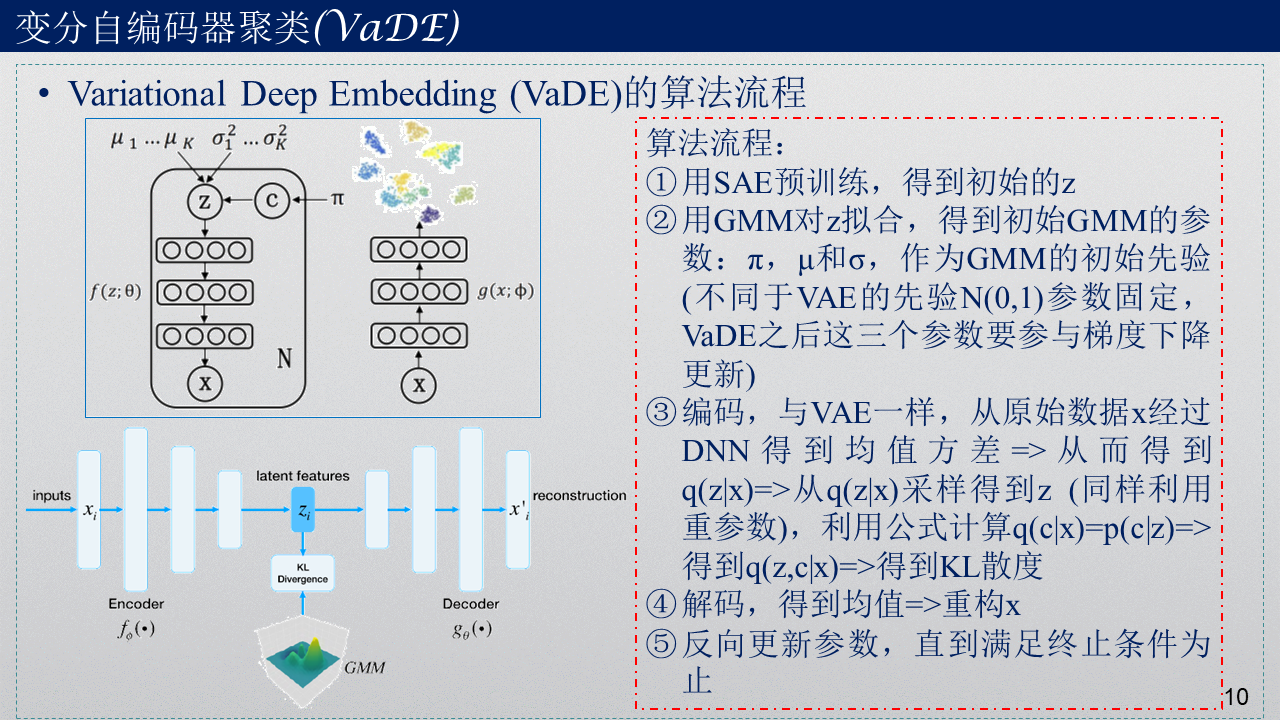
4. 疑问
1)GMM算法的参数pi并没有进行归一化处理,在更新过程中能保证pi的和始终为1吗?这个问题在作者评论里面有回答,说pi相比于参数miu, sigma来说,对结果影响不大,但又有人问了,如果遇到非平衡数据呢?这种情况下pi的影响还是比较大的。在代码里也不难实现,加一行代码,类似于pi/sum(pi)就行。
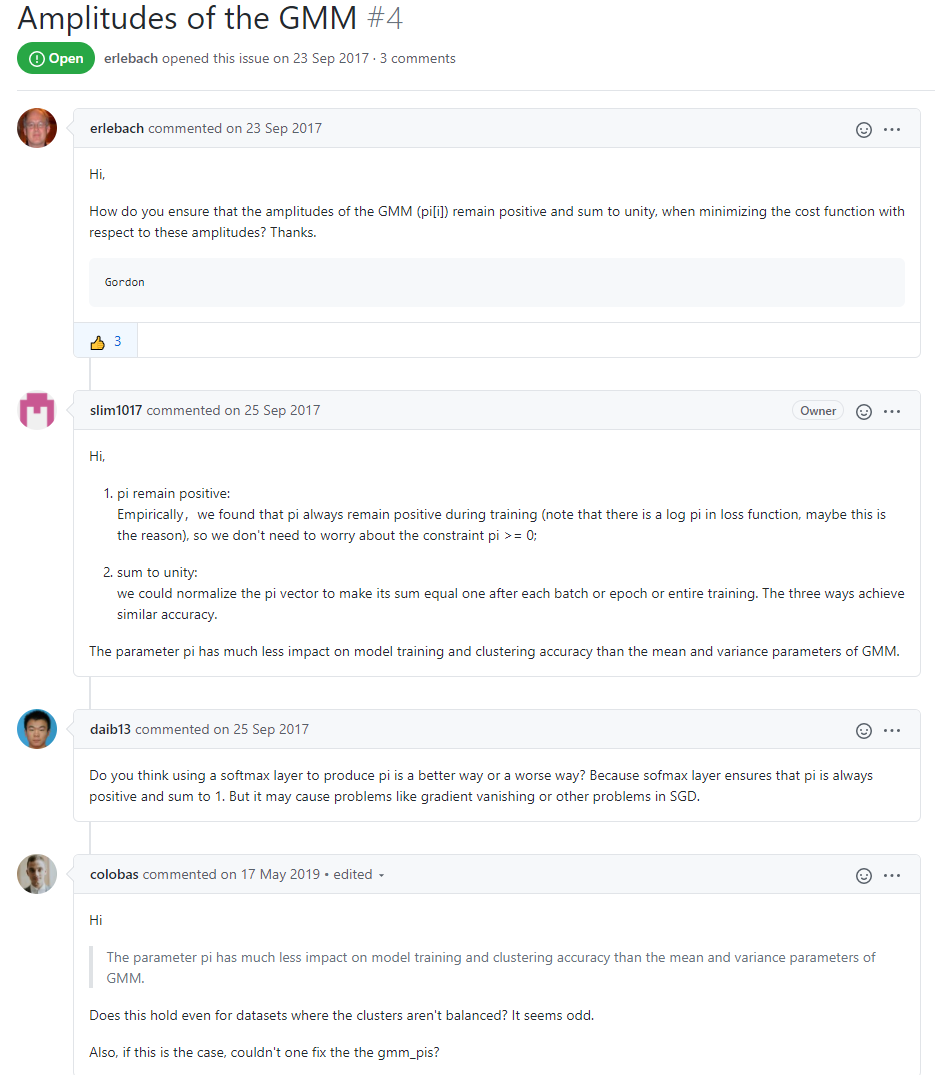
2)后验概率γ在代码里并不参与更新,为什么不和GMM的其他参数(pi, miu, sigma)一样进行梯度下降更新呢?而是直接套公式?有什么数学依据吗?这个在作者评论里面有人提到过,但是未被回复。其实直接ELBO目标对γ求偏导令其为0,用这种求极值的方式求解γ也没有问题,最后记得对γ进行归一化。
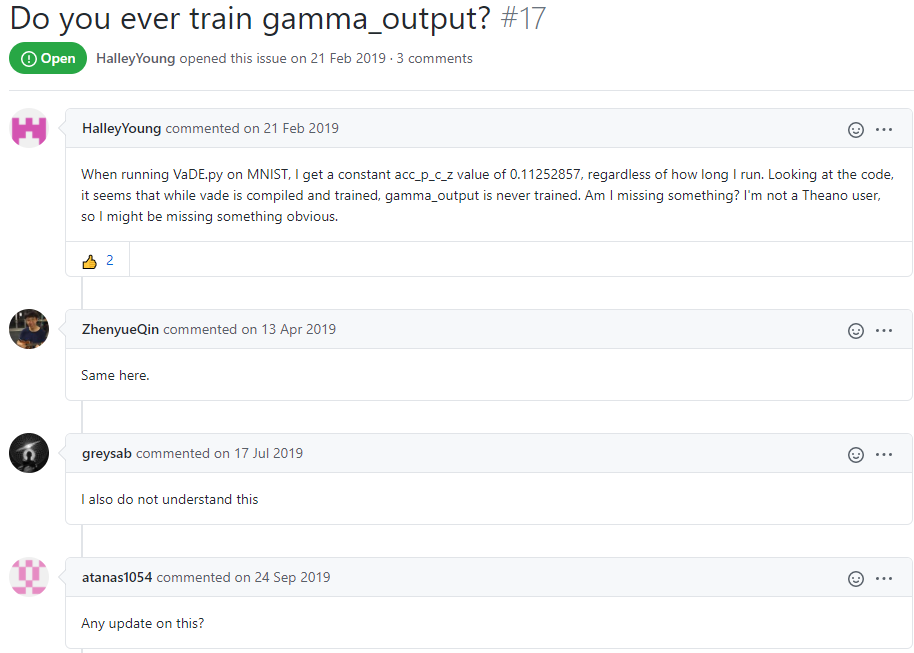
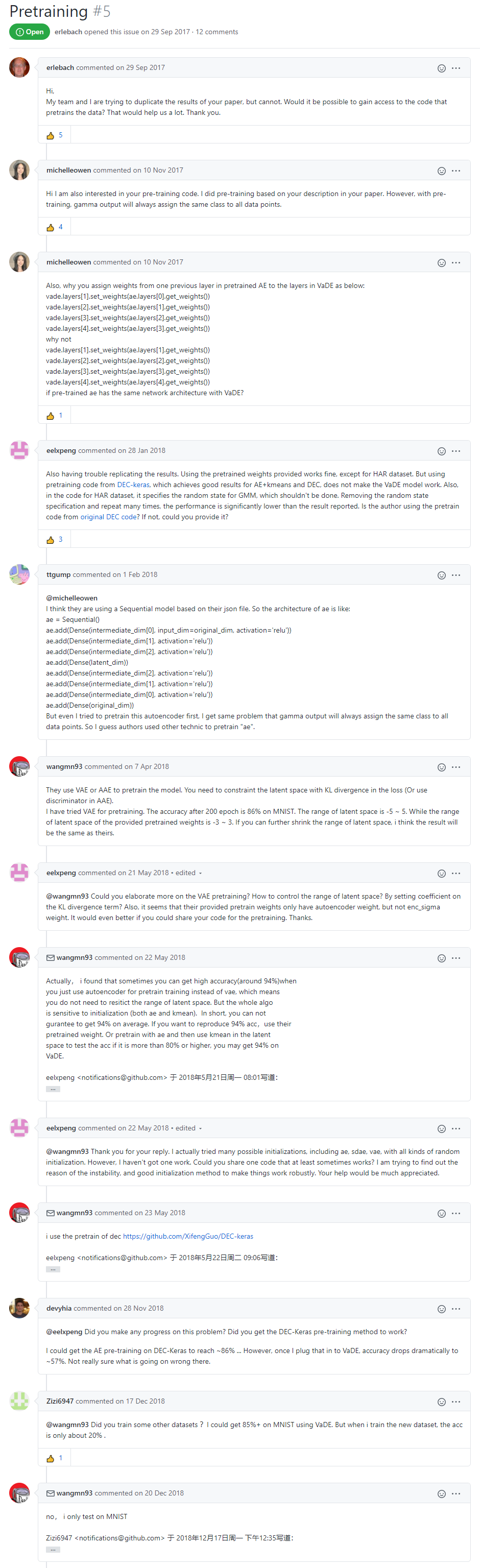
3)预训练到底是怎么做到的,仅仅是用SAE训练得到的结果吗?原作者代码里面只给出了预训练之后得到的具体参数,并没有给出预训练的代码。预训练这个问题在作者评论里面有被提到。预训练阶段还是非常关键的一步,当然,有人是这样做的:预训练使用VAE模型。
4) 代码中生成z的方式与VAE一模一样,而原文中的图示以及3.1节部分中的描述是z从${\mu }_c$与${\sigma }_c$而来,而公式(14)又与VAE一致了,原文中的表述并不统一,且代码与原文部分表述不符。
论文中说的是$\pi $、${\mu }_c$与${\sigma }_c$用GMM来初始化,代码里分别初始化为取平均、零矩阵、单位矩阵。不过问题也不大,自己改一下代码就OK。
如果能解决我的疑问,欢迎在评论区回复,一起探讨~
5. 参考文献
[3] Jiang Z , Zheng Y , Tan H , et al. Variational Deep Embedding: An Unsupervised and Generative Approach to Clustering. 2016.
[4] VaDE代码:
GitHub - slim1017/VaDE: Python code for paper - Variational Deep Embedding : A Generative Approach to Clustering
GitHub - GuHongyang/VaDE-pytorch: the reproduce of Variational Deep Embedding : A Generative Approach to Clustering Requirements by pytorch


