变分推断与变分自编码器
作者:凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/
本文主要介绍变分自编码器(Variational Auto-Encoder, VAE)及其推导过程,但变分自编码器涉及一些概率统计的基础知识,因此为了更好地理解变分自编码器,首先介绍变分推断(Variational Inference)与期望最大化(Expectation-Maximization, EM)算法,进而介绍变分自编码器,并给出另一种理解方法(参考文献[3])。
1. 变分推断




2. 变分自编码器




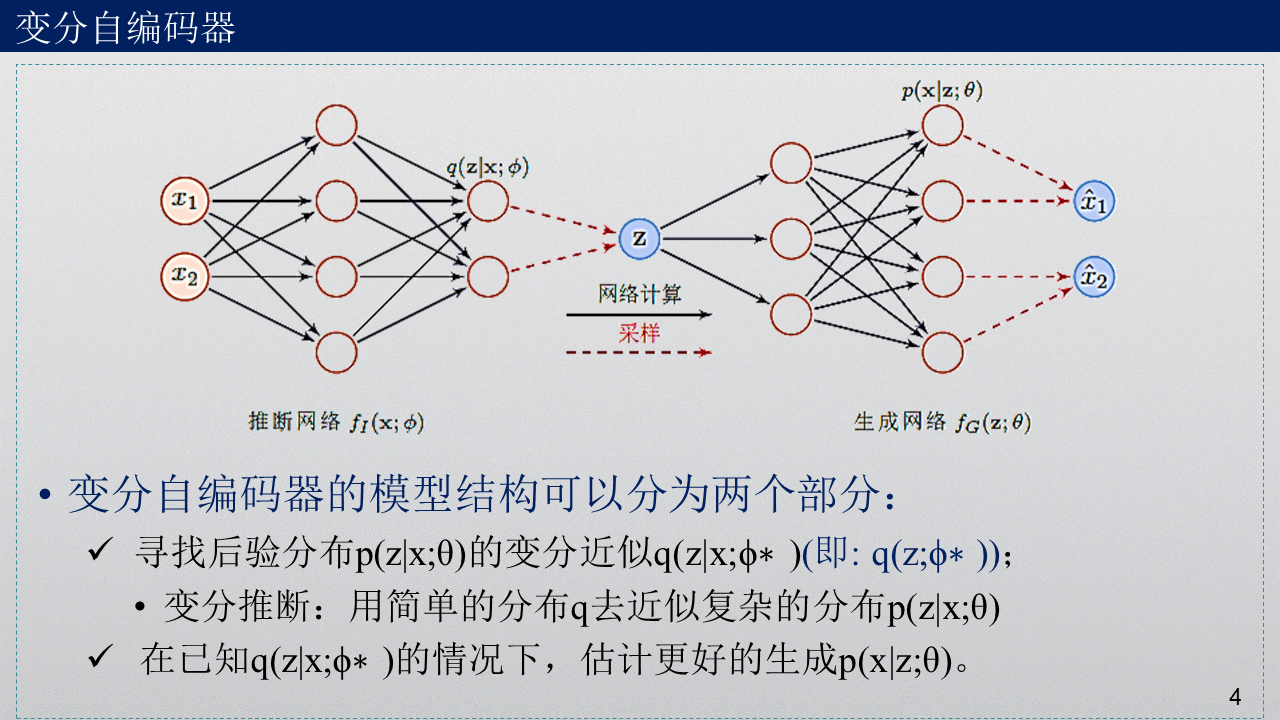


一般情况下,只采一个样即可,即K=1。详见参考文献[3]。


代码里z是这样的来的:$z \sim \mu +\varepsilon {{e}^{0.5\ln ({{\sigma }^{2}})}}=\mu +\varepsilon \sigma $

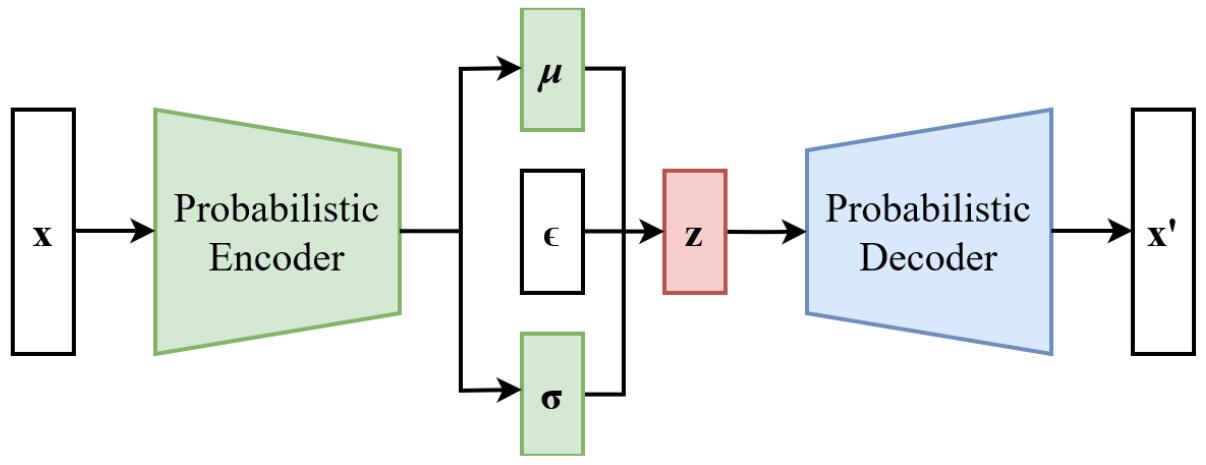
3. 变分自编码器另一种理解——直面联合分布



4. KL散度公式推导


5. 参考文献
[1] 变分贝叶斯 - 凯鲁嘎吉 - 博客园
[2] 邱锡鹏, 神经网络与深度学习[M]. 2019.
[3] 标签 vae 下的文章 - 科学空间|Scientific Spaces
[4] Kingma D P , Welling M . Auto-Encoding Variational Bayes[J]. 2013.
[5] 变分推断详细请参考:华俊豪博客-变分推理、变分贝叶斯算法理解与推导
[6] Tutorial - What is a variational autoencoder? – Jaan Altosaar https://jaan.io/what-is-variational-autoencoder-vae-tutorial/
[7] CS 285, Variational Inference and Generative Models, http://rail.eecs.berkeley.edu/deeprlcourse-fa20/static/slides/lec-18.pdf
[8] Ankush Ganguly, Samuel W. F. Earp, An Introduction to Variational Inference, 2021. https://arxiv.org/pdf/2108.13083.pdf

