MATLAB用“fitgmdist”函数拟合高斯混合模型(一维数据)
作者:凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/
在MATLAB中“fitgmdist”的用法及其GMM聚类算法中介绍过"fitgmdist"函数的用法,这次用"fitgmdist"拟合一维数据。
1. 一维高斯混合数据的产生
function data=generate_GMM() %前两列是数据,最后一列是类标签 %数据规模 N=300; %数据维度 % dim=1; %% %混合比例 para_pi=[0.3 0.2 0.5]; %第一类数据 mul=0; % 均值 S1=1; % 协方差 data1=mvnrnd(mul, S1, para_pi(1)*N); % 产生高斯分布数据 %第二类数据 mu2=4; S2=2; data2=mvnrnd(mu2,S2,para_pi(2)*N); %第三类数据 mu3=-4; S3=1; data3=mvnrnd(mu3,S3,para_pi(3)*N); data = [data1, ones(para_pi(1)*N,1); data2, 2*ones(para_pi(2)*N,1); data3, 3*ones(para_pi(3)*N,1)]; save data_gauss data
2. 拟合高斯混合模型
load data_gauss
data=data(:,1);
K=3;
gmm=fitgmdist(data, K);
% 自定义参数
% RegularizationValue=0.001; %正则化系数,协方差矩阵求逆
% MaxIter=1000; %最大迭代次数
% TolFun=1e-8; %终止条件
% gmm=fitgmdist(data, K, 'RegularizationValue', RegularizationValue, 'CovarianceType', 'diagonal', 'Start', 'plus', 'Options', statset('Display', 'final', 'MaxIter', MaxIter, 'TolFun', TolFun));
[N, D]=size(data);
mu=gmm.mu; %均值
Sigma=gmm.Sigma; %协方差矩阵
ComponentProportion=gmm.ComponentProportion; %混合比例
Y=zeros(N, K);
for k=1:K
Y(:,k)=ComponentProportion(k).*normpdf(data, mu(k), Sigma(:,:,k));
end
YY=sum(Y, 2);
plot(data,YY,'r.')
或者对数据排一下顺序:
load data_gauss
data=data(:,1);
K=3;
gmm=fitgmdist(data, K);
% 自定义参数
% RegularizationValue=0.001; %正则化系数,协方差矩阵求逆
% MaxIter=1000; %最大迭代次数
% TolFun=1e-8; %终止条件
% gmm=fitgmdist(data, K, 'RegularizationValue', RegularizationValue, 'CovarianceType', 'diagonal', 'Start', 'plus', 'Options', statset('Display', 'final', 'MaxIter', MaxIter, 'TolFun', TolFun));
[N, D]=size(data);
mu=gmm.mu; %均值
Sigma=gmm.Sigma; %协方差矩阵
ComponentProportion=gmm.ComponentProportion; %混合比例
Y=zeros(N, K);
for k=1:K
Y(:,k)=ComponentProportion(k).*normpdf(data, mu(k), Sigma(:,:,k));
end
YY=sum(Y, 2);
[X, index] = sort(data);
YY = YY(index);
plot(X,YY,'r-')
3. 结果
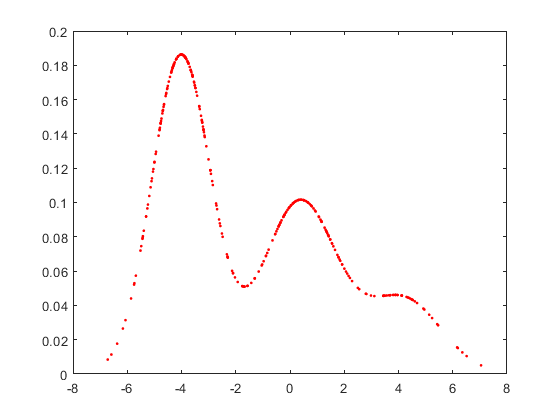
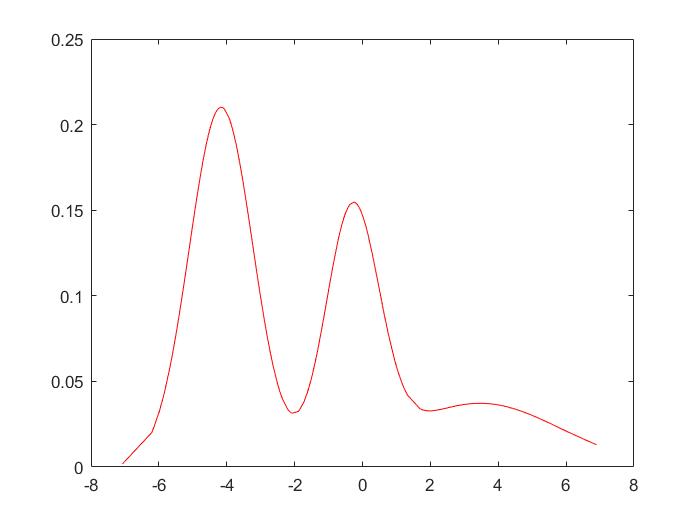
注意:这两个图不一样的原因是产生的数据每次都是随机的,我用的两组不同的数据得到的结果。
4. 参考
[1] MATLAB高斯混合数据的生成

