canopy聚类算法的MATLAB程序
凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/
1. canopy聚类算法简介
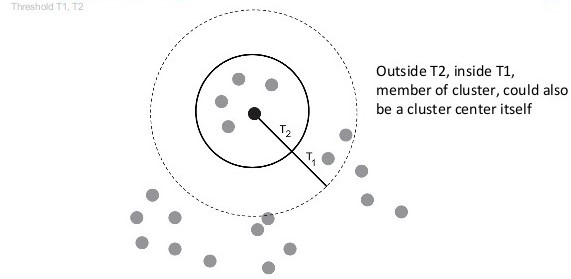
Canopy聚类算法是一个将对象分组到类的简单、快速、精确地方法。每个对象用多维特征空间里的一个点来表示。这个算法使用一个快速近似距离度量和两个距离阈值T1>T2来处理。基本的算法是,从一个点集合开始并且随机删除一个,创建一个包含这个点的Canopy,并在剩余的点集合上迭代。对于每个点,如果它的距离第一个点的距离小于T1,然后这个点就加入这个聚集中。除此之外,如果这个距离<T2,然后将这个点从这个集合中删除。这样非常靠近原点的点将避免所有的未来处理,不可以再做其它Canopy的中心。这个算法循环到初始集合为空为止,聚集一个集合的Canopies,每个可以包含一个或者多个点。每个点可以包含在多于一个的Canopy中。
Canopy算法其实本身也可以用于聚类,但它的结果可以为之后代价较高聚类提供帮助,其用在数据预处理上要比单纯拿来聚类更有帮助。Canopy聚类经常被用作更加严格的聚类技术的初始步骤,像是K均值聚类。建立canopies之后,可以删除那些包含数据点数目较少的canopy,往往这些canopy是包含孤立点的。
Canopy算法的步骤如下:
(1) 将所有数据放进list中,选择两个距离,T1,T2,T1>T2
(2)While(list不为空)
{
随机选择一个节点做canopy的中心;并从list删除该点;
遍历list:
对于任何一条记录,计算其到各个canopy的距离;
如果距离<T2,则给此数据打上强标记,并从list删除这条记录;
如果距离<T1,则给此数据打上弱标记;
如果到任何canopy中心的距离都>T1,那么将这条记录作为一个新的canopy的中心,并从list中删除这个元素;
}
需要注意的是参数的调整:
当T1过大时,会使许多点属于多个Canopy,可能会造成各个簇的中心点间距离较近,各簇间区别不明显;
当T2过大时,增加强标记数据点的数量,会减少簇个个数;T2过小,会增加簇的个数,同时增加计算时间;
2. MATLAB程序
clear
clc
%%%%%%%%%%%%%%% 加载数据 %%%%%%%%%%%%%%%%%%
X = dlmread('iris.data');
[~,X_dim]=size(X);
X=X(:,1:X_dim-1);
[num,dim] = size(X);
N=100;
k=zeros(N,1);
for t=1:N
%%%%%%%%%%%%%%% 抽样 %%%%%%%%%%%%%%%%%%
sample=round(num/10);
rand_array=randperm(num);
X_part=X(rand_array(1:sample),:);
D=pdist(X_part);
miu=mean(D);
sigma=std(D);
T2=miu+5*sigma;
K_max=20;
%%%%%%%%%canopy 自动划分聚类中心和个数%%%%%%%%%
k(t) = 0;
YB=[X zeros(num,1)];
Centr=zeros(K_max,dim);
while size(YB,1) && (k(t)<K_max)
k(t)=k(t)+1;
Centr(k(t),:)=YB(1,1:dim);
YB(1,:)=[]; %在选取第一个点为聚类点并删除
L=size(YB,1);
if L
dist1=(YB(:,1:dim)-ones(L,1)*Centr(k(t),1:dim)).^2; %计算欧式距离
dist2=sum(dist1,2);
end
for i=1:L-1
if(dist2(i)<T2) %<T2说明是该类,在矩阵中删除
YB(i,dim+1)=1;
end
end
YB(YB(:,dim+1)==1,:)=[]; %删除已归类的元素
end
end
tabulate(k(:))
数据见:MATLAB实例:PCA降维中的iris数据集,保存为:iris.data,最后一列是类标签。
3. 结果
Value Count Percent
1 0 0.00%
2 0 0.00%
3 99 99.00%
4 0 0.00%
5 1 1.00%
K=3为最终结果。注意:实验结果与T2的选取有很大关系,视具体数据而定。


