受限玻尔兹曼机(Restricted Boltzmann Machine)
作者:凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/


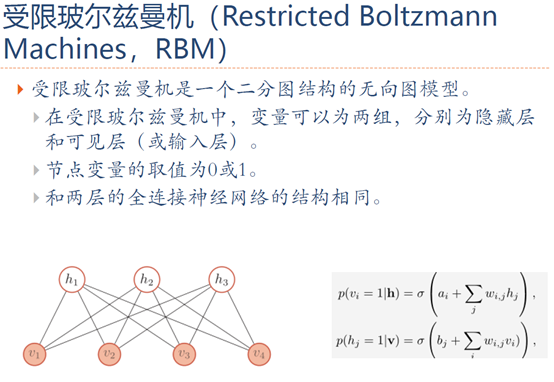
1. 生成模型


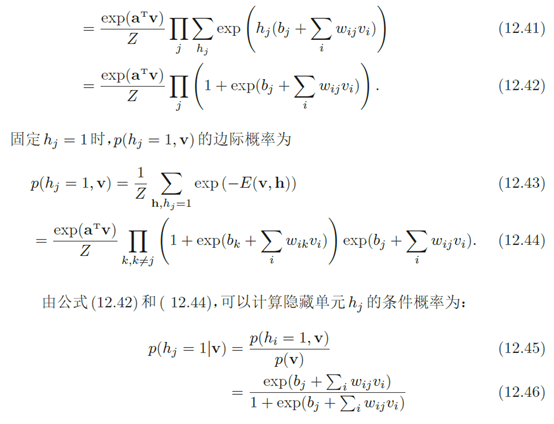

2. 参数学习


3. 对比散度学习算法
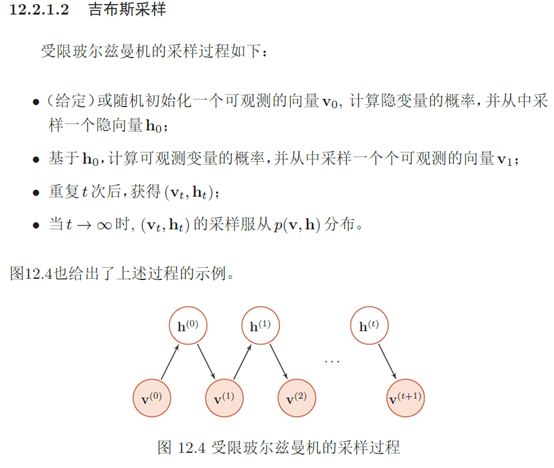
由于受限玻尔兹曼机的特殊结构,因此可以使用一种比吉布斯采样更有效 的学习算法,即对比散度(Contrastive Divergence)对比散度算法仅需k步吉布斯采样。为了提高效率,对比散度算法用一个训练样本作为可观测向量的初始值。然后,交替对可观测向量和隐藏向量进行吉布斯采样,不需要等到收敛,只需要k步就足够了。这就是CD-k 算法。通常,k = 1就可以学得很好。对比散度的流程如算法12.1所示。

4. MATLAB程序解读
% maxepoch -- 最大迭代次数maximum number of epochs
% numhid -- 隐含层神经元数number of hidden units
% batchdata -- 分批后的训练数据集the data that is divided into batches (numcases numdims numbatches)
% restart -- 如果从第1层开始学习,就置restart为1set to 1 if learning starts from beginning
%作用:训练RBM,利用1步CD算法 直接调用权值迭代公式不使用反向传播
%可见的、二元的、随机的像素通过对称加权连接连接到隐藏的、二元的、随机的特征检测器
epsilonw = 0.1; % Learning rate for weights 权重学习率 alpha
epsilonvb = 0.1; % Learning rate for biases of visible units 可视层偏置学习率 alpha
epsilonhb = 0.1; % Learning rate for biases of hidden units 隐藏层偏置学习率 alpha
weightcost = 0.0002; %权衰减,用于防止出现过拟合
initialmomentum = 0.5; %动量项学习率,用于克服收敛速度和算法的不稳定性之间的矛盾
finalmomentum = 0.9;
[numcases numdims numbatches]=size(batchdata);%[numcases numdims numbatches]=[每批中的样本数 每个样本的维数 训练样本批数]
if restart ==1 %是否为重新开始即从头训练
restart=0;
epoch=1;
% Initializing symmetric weights and biases. 初始化权重和两层偏置
vishid = 0.1*randn(numdims, numhid);% 连接权值Wij 784*1000
hidbiases = zeros(1,numhid);% 隐含层偏置项bi
visbiases = zeros(1,numdims);% 可视化层偏置项aj
poshidprobs = zeros(numcases,numhid); %样本数*隐藏层NN数,隐藏层输出p(h1|v0)对应每个样本有一个输出 100*1000
neghidprobs = zeros(numcases,numhid); %重构数据驱动的隐藏层
posprods = zeros(numdims,numhid); % 表示p(h1|v0)*v0,用于更新Wij即<vihj>data 784*1000
negprods = zeros(numdims,numhid); %<vihj>recon
vishidinc = zeros(numdims,numhid); % 权值更新的增量 ΔW
hidbiasinc = zeros(1,numhid); % 隐含层偏置项更新的增量 1*1000 Δb
visbiasinc = zeros(1,numdims); % 可视化层偏置项更新的增量 1*784 Δa
batchposhidprobs=zeros(numcases,numhid,numbatches); % 整个数据隐含层的输出 每批样本数*隐含层维度*批数
end
for epoch = epoch:maxepoch %每个迭代周期
fprintf(1,'epoch %d\r',epoch);
errsum=0;
for batch = 1:numbatches %每一批样本
fprintf(1,'epoch %d batch %d\r',epoch,batch);
%%CD-1
%%%%%%%%% START POSITIVE PHASE 正向梯度%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
data = batchdata(:,:,batch); %data里是100个图片数据
poshidprobs = 1./(1 + exp(-data*vishid - repmat(hidbiases,numcases,1))); %隐藏层输出p(h=1|v0)=sigmod函数=1/(1+exp(-wx-b)) 根据这个分布采集一个隐变量h
batchposhidprobs(:,:,batch)=poshidprobs; %将输出存入一个三位数组
posprods = data' * poshidprobs; %p(h|v0)*v0 更新权重时会使用到 计算正向梯度vh'
poshidact = sum(poshidprobs); %隐藏层中神经元概率和,在更新隐藏层偏置时会使用到
posvisact = sum(data); %可视层中神经元概率和,在更新可视层偏置时会使用到
%%%%%%%%% END OF POSITIVE PHASE %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%gibbs采样
poshidstates = poshidprobs > rand(numcases,numhid); %将隐藏层输出01化表示,大于随机概率的置1,小于随机概率的置0,gibbs抽样,设定状态
%%%%%%%%% START NEGATIVE PHASE 反向梯度%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
negdata = 1./(1 + exp(-poshidstates*vishid' - repmat(visbiases,numcases,1))); %01化表示之后算vt=p(vt|ht-1)重构的数据 p(v=1|h)=sigmod(W*h+a) 采集重构的可见变量v'
neghidprobs = 1./(1 + exp(-negdata*vishid - repmat(hidbiases,numcases,1))); %ht=p(h|vt)使用重构数据隐藏层的输出 p(h=1|v)=sigmod(W'*v+b) 采样一个h'
negprods = negdata'*neghidprobs; %计算反向梯度v'h';
neghidact = sum(neghidprobs);
negvisact = sum(negdata);
%%%%%%%%% END OF NEGATIVE PHASE %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%更新参数
err= sum(sum( (data-negdata).^2 )); %整批数据的误差 ||v-v'||^2
errsum = err + errsum;
if epoch>5 %迭代次数不同调整冲量
momentum=finalmomentum;
else
momentum=initialmomentum;
end
%%%%%%%%% UPDATE WEIGHTS AND BIASES 更新权重和偏置%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
vishidinc = momentum*vishidinc + ...
epsilonw*( (posprods-negprods)/numcases - weightcost*vishid); %权重的增量 ΔW=alpha*(vh'-v'h')
visbiasinc = momentum*visbiasinc + (epsilonvb/numcases)*(posvisact-negvisact); %可视层增量 Δa=alpha*(v-v')
hidbiasinc = momentum*hidbiasinc + (epsilonhb/numcases)*(poshidact-neghidact); %隐含层增量 Δb=alpha*(h-h')
vishid = vishid + vishidinc; %a=a+Δa
visbiases = visbiases + visbiasinc; %W=W+ΔW
hidbiases = hidbiases + hidbiasinc; %b=b+Δb
%%%%%%%%%%%%%%%% END OF UPDATES %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
end
fprintf(1, 'epoch %4i error %6.1f \n', epoch, errsum);
end
5. 玻尔兹曼机与受限玻尔兹曼机
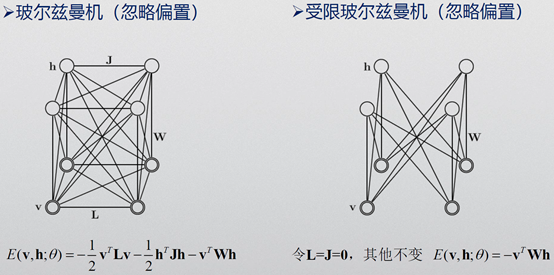
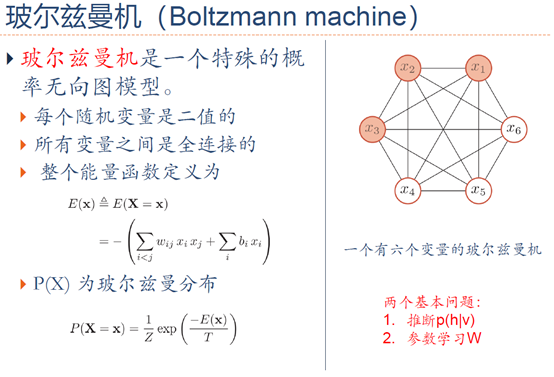



6. 参考文献
[1] 邱锡鹏, 神经网络与深度学习[M]. 2019.
[2] Salakhutdinov R, Hinton G. Deep boltzmann machines[C]//Artificial intelligence and statistics. 2009: 448-455.
[3] Hinton, Training a deep autoencoder or a classifier on MNIST digits. 2006.
[4] Hinton G E. Training products of experts by minimizing contrastive divergence[J]. Neural computation, 2002, 14(8): 1771-1800.
[5] Hinton G E. A practical guide to training restricted Boltzmann machines[M]//Neural networks: Tricks of the trade. Springer, Berlin, Heidelberg, 2012: 599-619.

