Gaussian field consensus论文解读及MATLAB实现
作者:凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/
一、Introduction
论文:Wang G , Chen Y , Zheng X . Gaussian field consensus: A robust nonparametric matching method for outlier rejection[J]. Pattern Recognition, 2018, 74:305-316.
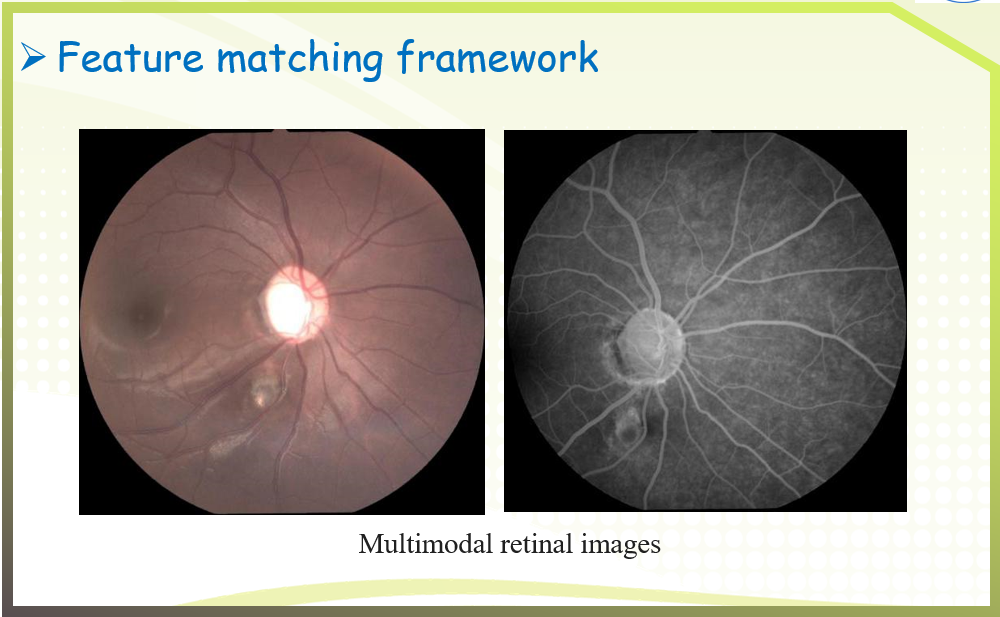

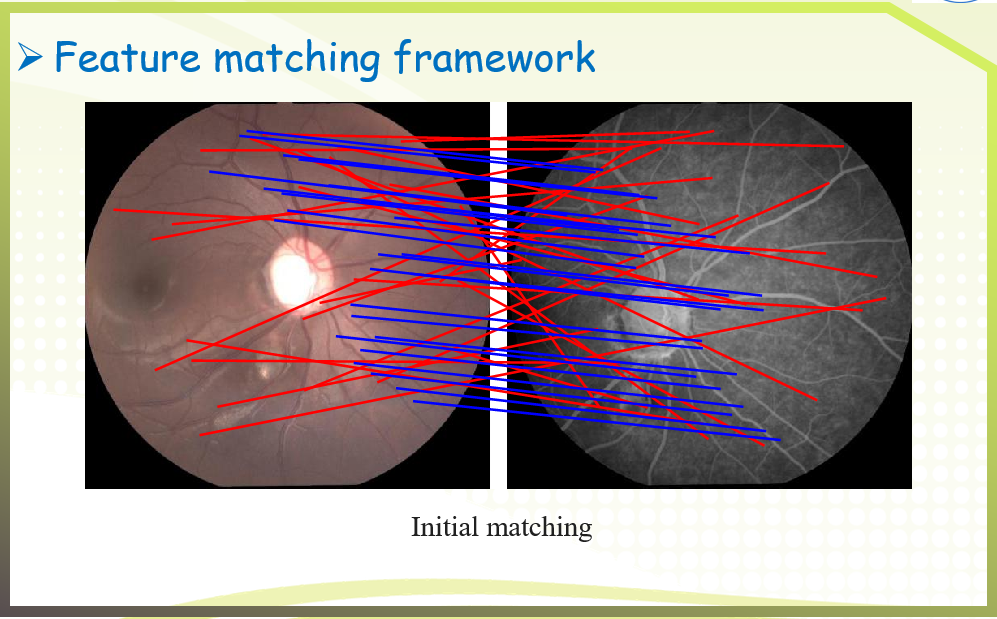
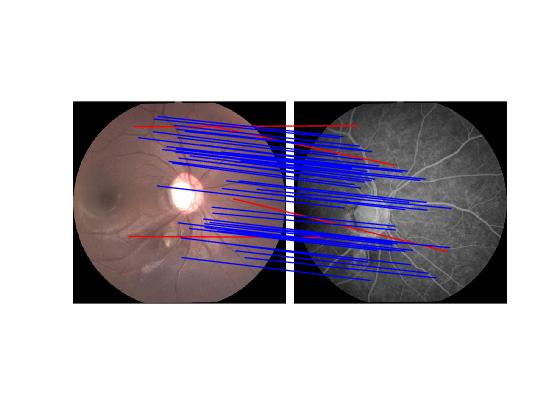
An image pair and its putative correspondences. Blue and red lines represent inliers and outliers respectively.


二、GFC algorithm

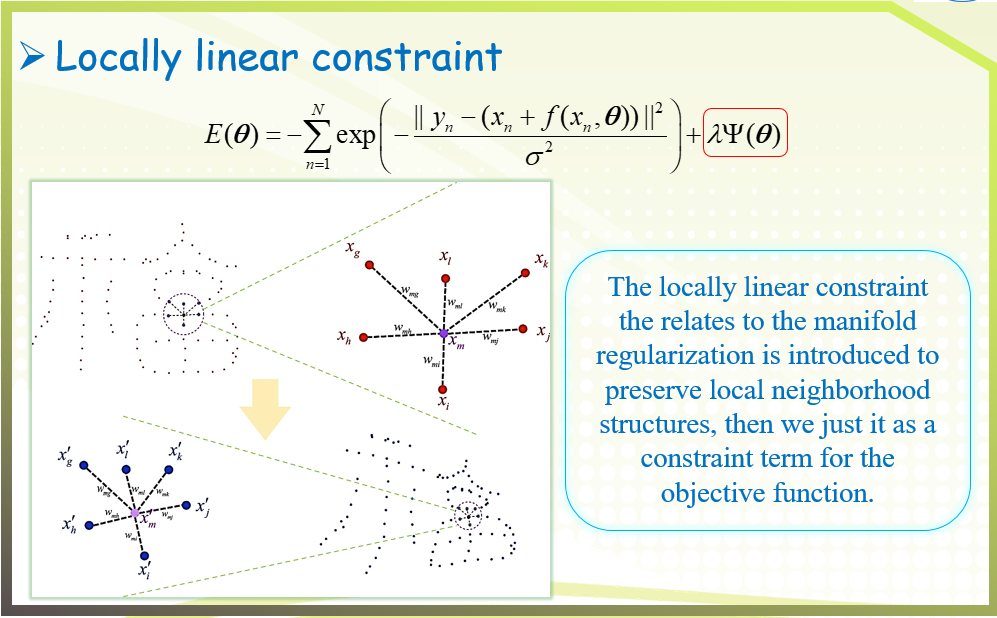

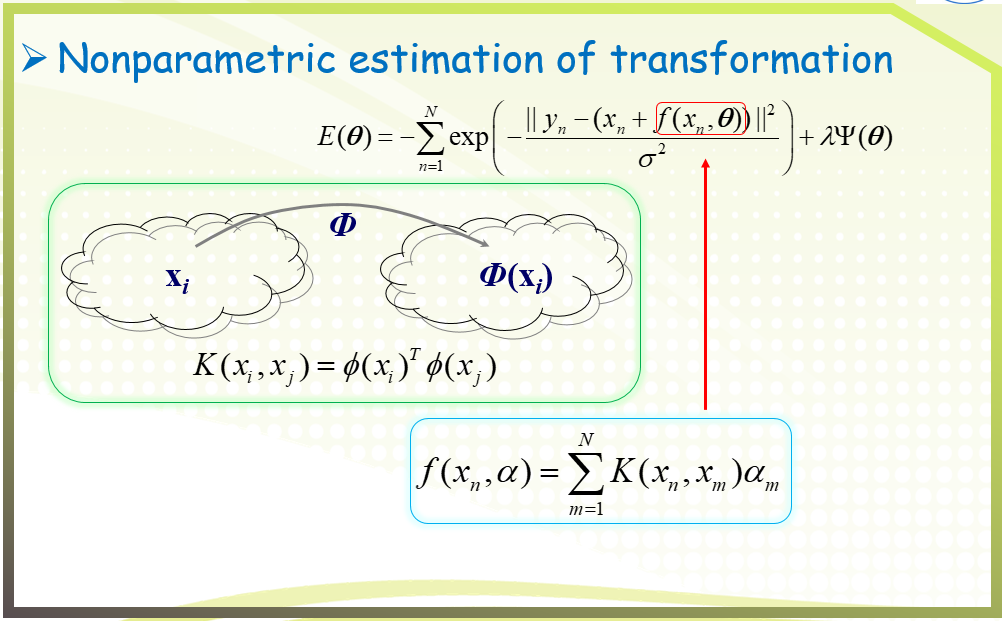


三、Experimental results

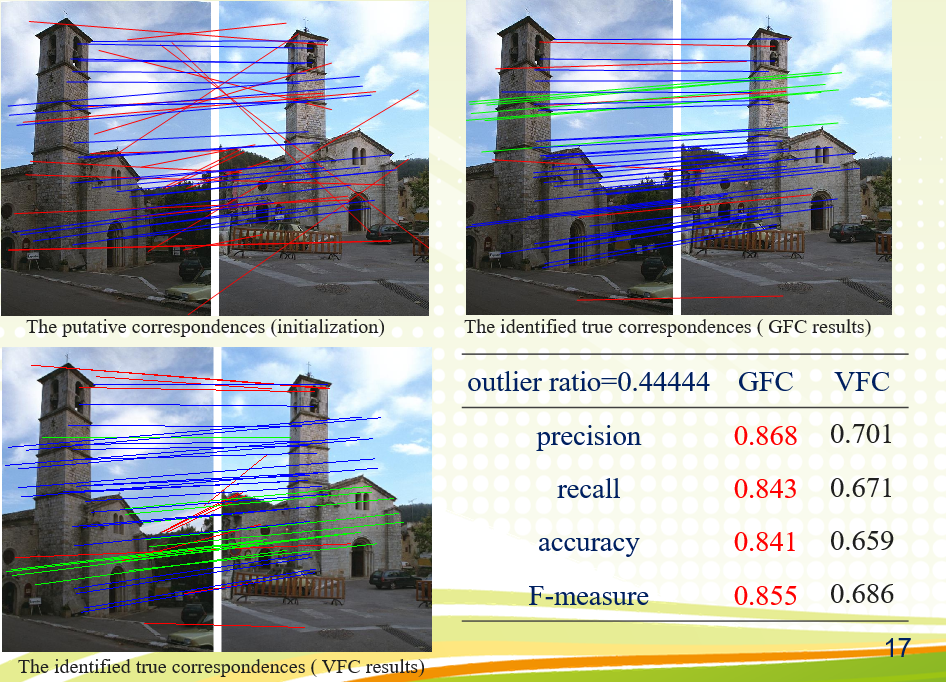
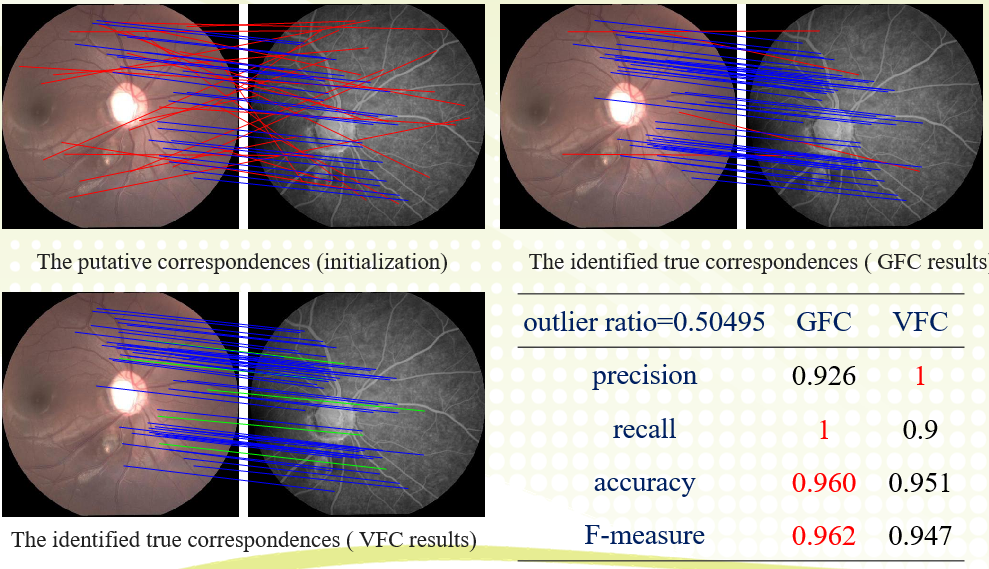
四、Conclusion

五、Code
results.m
function criterion=results()
% GFC;
% 读取图像及对应关系数据
% church
% ImgName1 = './TestData/church1.jpg' ;
% ImgName2 = './TestData/church2.jpg' ;
% load('./TestData/church.mat');
% eye
ImgName1 = './TestData/14_a.jpg' ;
ImgName2 = './TestData/14_b.jpg' ;
load('./TestData/14_20.mat');
I1 = imread(ImgName1) ;
I2 = imread(ImgName2) ;
t0=cputime;
[precision, recall, accuracy, f1]=demo_GFC(I1, I2, X, Y, CorrectIndex);
run_time=cputime-t0;
criterion=[precision; recall; accuracy; f1; run_time];
demo_GFC.m
function [precision, recall, accuracy, f1]=demo_GFC(I1, I2, X, Y, CorrectIndex) label=CorrectIndex; delta =0.5; [index] = GFC_match(X,Y,delta); [precision, recall, accuracy, f1] = evaluatePR(label, index, size(X,1)); % Plot results %原始结果 % N=size(X); % temp=1:N; % temp=temp'; % plot_matches(I1, I2, X, Y, temp, label); %实验结果 plot_matches(I1, I2, X, Y, index, label);
adjacency.m
function A = adjacency(DATA, TYPE, PARAM, DISTANCEFUNCTION);
% Compute the adjacency graph of the data set DATA
%
% A = adjacency(DATA, TYPE, PARAM, DISTANCEFUNCTION);
%
% DATA - NxK matrix. Data points are rows.
% TYPE - string 'nn' or string 'epsballs'.
% PARAM - integer if TYPE='nn', real number if TYPE='epsballs'.
% DISTANCEFUNCTION - function mapping a (DxM) and a (D x N) matrix
% to an M x N distance matrix (D:dimensionality)
% Returns: A, sparse symmetric NxN matrix of distances between the
% adjacent points.
%
% Example:
%
% A = adjacency(X,'nn',6)
% A contains the adjacency matrix for the data
% set X. For each point, the distances to 6 adjacent points are
% stored. N
%
% Note: the adjacency relation is symmetrized, i.e. if
% point a is adjacent to point b, then point b is also considered to be
% adjacent to point a.
%
%
% Author:
%
% Mikhail Belkin
% misha@math.uchicago.edu
%
% Modified by: Vikas Sindhwani
% June 2004
% disp('Computing Adjacency Graph');
if (nargin < 3) | (strcmp(TYPE,'nn') & strcmp(TYPE,'epsballs')) | ~isreal(PARAM)
disp(sprintf('ERROR: Too few arguments given or incorrect arguments.\n'));
disp(sprintf('USAGE:\n A = laplacian(DATA, TYPE, PARAM)'));
disp(sprintf('DATA - the data matrix. Data points are rows.'));
disp(sprintf('Nearest neigbors: TYPE =''nn'' PARAM = number of nearest neigbors'));
disp(sprintf('Epsilon balls: TYPE =''epsballs'' PARAM = redius of the ball\n'));
return;
end
n = size(DATA,1);
%disp (sprintf ('DATA: %d points in %d dimensional space.',n,size (DATA,2)));
switch TYPE
case {'nn'}
% disp(sprintf('Creating the adjacency matrix. Nearest neighbors, N=%d.', PARAM));
case{'eps', 'epsballs'}
%disp(sprintf('Creating the adjacency matrix. Epsilon balls, eps=%f.', PARAM));
end;
A = sparse(n,n);
step = 100;
if (strcmp(TYPE,'nn'))
for i1=1:step:n
i2 = i1+step-1;
if (i2> n)
i2=n;
end;
XX= DATA(i1:i2,:);
dt = feval(DISTANCEFUNCTION, XX',DATA');
[Z,I] = sort ( dt,2);
for i=i1:i2
if ( mod(i, 500) ==0)
%disp(sprintf('%d points processed.', i));
end;
for j=2:PARAM+1
A(i,I(i-i1+1,j))= Z(i-i1+1,j);
A(I(i-i1+1,j),i)= Z(i-i1+1,j);
end;
end
end;
% epsilon balls
else
for i1=1:step:n
i2 = i1+step-1;
if (i2> n)
i2=n;
end;
XX= DATA(i1:i2,:);
dt = feval(DISTANCEFUNCTION, XX',DATA');
[Z,I] = sort ( dt,2 );
for i=i1:i2
% if ( mod(i, 500) ==0) disp(sprintf('%d points processed.', i)); end;
j=2;
while ( (Z(i-i1+1,j) < PARAM))
j = j+1;
jj = I(i-i1+1,j);
A(i,jj)= Z(i-i1+1,j);
A(jj,i)= Z(i-i1+1,j);
end;
end
end;
end;
con_K.m
function K=con_K(x,y,beta)
if nargin<3
error('Error! Not enough input parameters.');
end
ks=-2 * beta^2;
[n, d]=size(x);
[m, d]=size(y);
K=repmat(x,[1 1 m])-permute(repmat(y,[1 1 n]),[3 2 1]);
K=squeeze(sum(K.^2,2));
K=K/ks;
K=exp(K);
costfun_GFC.m
function [E, G] = costfun_GFC(param, X, Y, U, beta,lambda,sigma2)
[N, D] = size(X);
M = size(U, 2);
Alpha = reshape(param, [M D]);
options=ml_options('Kernel','rbf', 'KernelParam', beta,'NN',5);
options.GraphWeights= 'heat';
options.GraphWeightParam=sqrt(sigma2);
L=laplacian(X,'nn',options);
E=lambda * trace(Alpha'*U'*L*U*Alpha);
V = Y-(X+ U*Alpha);
a = -2 / N / (2*sigma2)^(D/2);
F = exp(-sum(V.^2, 2) / (2*sigma2));
E = E + a * sum(F);
G = -a * U' * ( V .* repmat(F, [1 D]) / sigma2 ) + 2*lambda * U'* L * U *Alpha;
euclidean.m
function d = euclidean(a,b,df)
% EUCLIDEAN - computes Euclidean distance matrix
%
% E = euclidean(A,B)
%
% A - (DxM) matrix
% B - (DxN) matrix
% df = 1, force diagonals to be zero; 0 (default), do not force
%
% Returns:
% E - (MxN) Euclidean distances between vectors in A and B
%
%
% Description :
% This fully vectorized (VERY FAST!) m-file computes the
% Euclidean distance between two vectors by:
%
% ||A-B|| = sqrt ( ||A||^2 + ||B||^2 - 2*A.B )
%
% Example :
% A = rand(400,100); B = rand(400,200);
% d = distance(A,B);
% Author : Roland Bunschoten
% University of Amsterdam
% Intelligent Autonomous Systems (IAS) group
% Kruislaan 403 1098 SJ Amsterdam
% tel.(+31)20-5257524
% bunschot@wins.uva.nl
% Last Rev : Wed Oct 20 08:58:08 MET DST 1999
% Tested : PC Matlab v5.2 and Solaris Matlab v5.3
% Copyright notice: You are free to modify, extend and distribute
% this code granted that the author of the original code is
% mentioned as the original author of the code.
% Fixed by JBT (3/18/00) to work for 1-dimensional vectors
% and to warn for imaginary numbers. Also ensures that
% output is all real, and allows the option of forcing diagonals to
% be zero.
if (nargin < 2)
error('Not enough input arguments');
end
if (nargin < 3)
df = 0; % by default, do not force 0 on the diagonal
end
if (size(a,1) ~= size(b,1))
error('A and B should be of same dimensionality');
end
if ~(isreal(a)*isreal(b))
disp('Warning: running distance.m with imaginary numbers. Results may be off.');
end
if (size(a,1) == 1)
a = [a; zeros(1,size(a,2))];
b = [b; zeros(1,size(b,2))];
end
aa=sum(a.*a); bb=sum(b.*b); ab=a'*b;
d = sqrt(repmat(aa',[1 size(bb,2)]) + repmat(bb,[size(aa,2) 1]) - 2*ab);
% make sure result is all real
d = real(d);
% force 0 on the diagonal?
if (df==1)
d = d.*(1-eye(size(d)));
end
evaluatePR.m
function [precision, recall, accuracy, f1] = evaluatePR(CorrectIndex, Index, siz) tmp=zeros(1, siz); tmp(Index) = 1; tmp(CorrectIndex) = tmp(CorrectIndex)+1; GFCCorrect = find(tmp == 2); NumCorrectIndex = length(CorrectIndex); NumGFCIndex = length(Index); NumGFCCorrect = length(GFCCorrect); % corrRate = NumCorrectIndex/siz; precision = NumGFCCorrect/NumGFCIndex; TP=NumGFCCorrect; FP=NumGFCIndex-TP; recall = NumGFCCorrect/NumCorrectIndex; FN=NumCorrectIndex-TP; TN=siz-NumGFCIndex-FN; accuracy=(TP+TN)/(TP+TN+FP+FN); f1=(2*precision*recall)/(precision+recall);
GFC.m
function [idt, V , param] = GFC(X, Y, delta)
[N1, D] = size(X);
eta=0.98;
history.x = [ ];
history.fval = [ ];
beta =1.5;
lambda = 3;
sigma2=power(det(X'*X/N1), 1/(2^D));
M=round(sqrt(N1));
x0 = zeros(M*D, 1);
options = optimset( 'display','iter');
options = optimset(options, 'outputfcn',@GFCoutfun);
options = optimset( options, 'LargeScale','off');
options = optimset(options, 'MaxFunEvals', 100);
options = optimset(options, 'MaxIter', 100);
options = optimset(options, 'GradObj', 'on');
U=get_U(X,beta,M);
param = fminunc(@(x)costfun_GFC(x, X, Y, U, beta, lambda, sigma2), x0, options);
Alpha = reshape(param, [M D]);
V=X+U*Alpha;
Pb = exp(-sum((Y-V).^2, 2) / (sigma2)) ;
idt = find(Pb > delta);
function stop = GFCoutfun(x,optimValues,state,varargin)
stop = false;
switch state
case 'init'
case 'iter'
history.fval = [history.fval; optimValues.fval];
history.x = [history.x; reshape(x,1,length(x))];
Alpha = reshape(x, [M D]);
V=X+U*Alpha;
sigma2=sigma2 * eta;
case 'done'
otherwise
end
end
end
function U=get_U(X,beta,M)
tmp_X = unique(X, 'rows');
idx = randperm(size(tmp_X,1));
idx = idx(1:min(M,size(tmp_X,1)));
ctrl_pts=tmp_X(idx,:);
U = con_K(X, ctrl_pts, beta);
end
GFC_match.m
function [idt]=GFC_match(X,Y,delta)
Ni=2;
Xk=X;
k=1;
s=1;
while s
X2=Xk;Y2=Y;
normal.xm=0; normal.ym=0;
normal.xscale=1; normal.yscale=1;
[nX, nY, normal]=norm2s(X2,Y2);
[idt, trans] = GFC(nX,nY,delta);
trans=(trans)*normal.yscale+repmat(normal.ym,size(Y2,1),1);
Xk = trans;
if k==Ni
s=0;
else
k=k+1;
end
end
end
laplacian.m
function L = laplacian(DATA, TYPE, options)
% Calculate the graph laplacian of the adjacency graph of data set DATA.
%
% L = laplacian(DATA, TYPE, PARAM)
%
% DATA - NxK matrix. Data points are rows.
% TYPE - string 'nn' or string 'epsballs'
% options - Data structure containing the following fields
% NN - integer if TYPE='nn' (number of nearest neighbors),
% or size of 'epsballs'
%
% DISTANCEFUNCTION - distance function used to make the graph
% WEIGHTTYPPE='binary' | 'distance' | 'heat'
% WEIGHTPARAM= width for heat kernel
% NORMALIZE= 0 | 1 whether to return normalized graph laplacian or not
%
% Returns: L, sparse symmetric NxN matrix
%
% Author:
%
% Mikhail Belkin
% misha@math.uchicago.edu
%
% Modified by: Vikas Sindhwani (vikass@cs.uchicago.edu)
% June 2004
% disp('Computing Graph Laplacian.');
NN=options.NN;
DISTANCEFUNCTION=options.GraphDistanceFunction;
WEIGHTTYPE=options.GraphWeights;
WEIGHTPARAM=options.GraphWeightParam;
NORMALIZE=options.GraphNormalize;
% calculate the adjacency matrix for DATA
A = adjacency(DATA, TYPE, NN, DISTANCEFUNCTION);
W = A;
% disassemble the sparse matrix
[A_i, A_j, A_v] = find(A);
switch WEIGHTTYPE
case 'distance'
for i = 1: size(A_i)
W(A_i(i), A_j(i)) = A_v(i);
end;
case 'binary'
disp('Laplacian : Using Binary weights ');
for i = 1: size(A_i)
W(A_i(i), A_j(i)) = 1;
end;
case 'heat'
% disp(['Laplacian : Using Heat Kernel sigma : ' num2str(WEIGHTPARAM)]);
t=WEIGHTPARAM;
for i = 1: size(A_i)
W(A_i(i), A_j(i)) = exp(-A_v(i)^2/(2*t*t));
end;
otherwise
error('Unknown Weighttype');
end
D = sum(W(:,:),2);
if NORMALIZE==0
L = spdiags(D,0,speye(size(W,1)))-W;
else % normalized laplacian
D=diag(sqrt(1./D));
L=eye(size(W,1))-D*W*D;
end
ml_options.m
function options = ml_options(varargin)
% ML_OPTIONS - Generate/alter options structure for training classifiers
% ----------------------------------------------------------------------------------------%
% options = ml_options('PARAM1',VALUE1,'PARAM2',VALUE2,...)
%
% Creates an options structure "options" in which the named parameters
% have the specified values. Any unspecified parameters are set to
% default values specified below.
% options = ml_options (with no input arguments) creates an options structure
% "options" where all the fields are set to default values specified below.
%
% Example:
% options=ml_options('Kernel','rbf','KernelParam',0.5,'NN',6);
%
% "options" structure is as follows:
%
% Field Name: Description : default
% -------------------------------------------------------------------------------------
% 'Kernel': 'linear' | 'rbf' | 'poly' : 'linear'
% 'KernelParam': -- | sigma | degree : 1
% 'NN': number of nearest neighbor : 6
%'GraphDistanceFuncion': distance function for graph: 'euclidean' | 'cosine' : 'euclidean'
% 'GraphWeights': 'binary' | 'distance' | 'heat' : 'binary'
% 'GraphWeightParam': e.g For heat kernel, width to use : 1
% 'GraphNormalize': Use normalized Graph laplacian (1) or not (0) : 1
% 'ClassEdges': Disconnect Edges across classes:yes(1) no (0) : 0
% 'gamma_A': RKHS norm regularization parameter (Ambient) : 1
% 'gamma_I': Manifold regularization parameter (Intrinsic) : 1
% -------------------------------------------------------------------------------------
%
% Acknowledgement: Adapted from Anton Schwaighofer's software:
% http://www.cis.tugraz.at/igi/aschwaig/software.html
%
% Author: Vikas Sindhwani (vikass@cs.uchicago.edu)
% June 2004
% ----------------------------------------------------------------------------------------%
% options default values
options = struct('Kernel','linear', ...
'KernelParam',1, ...
'NN',6,...
'GraphDistanceFunction','euclidean',...
'GraphWeights', 'binary', ...
'GraphWeightParam',1, ...
'GraphNormalize',1, ...
'ClassEdges',0,...
'gamma_A',1.0,...
'gamma_I',1.0);
numberargs = nargin;
Names = fieldnames(options);
[m,n] = size(Names);
names = lower(Names);
i = 1;
while i <= numberargs
arg = varargin{i};
if isstr(arg)
break;
end
if ~isempty(arg)
if ~isa(arg,'struct')
error(sprintf('Expected argument %d to be a string parameter name or an options structure.', i));
end
for j = 1:m
if any(strcmp(fieldnames(arg),Names{j,:}))
val = getfield(arg, Names{j,:});
else
val = [];
end
if ~isempty(val)
[valid, errmsg] = checkfield(Names{j,:},val);
if valid
options = setfield(options, Names{j,:},val);
else
error(errmsg);
end
end
end
end
i = i + 1;
end
% A finite state machine to parse name-value pairs.
if rem(numberargs-i+1,2) ~= 0
error('Arguments must occur in name-value pairs.');
end
expectval = 0;
while i <= numberargs
arg = varargin{i};
if ~expectval
if ~isstr(arg)
error(sprintf('Expected argument %d to be a string parameter name.', i));
end
lowArg = lower(arg);
j = strmatch(lowArg,names);
if isempty(j)
error(sprintf('Unrecognized parameter name ''%s''.', arg));
elseif length(j) > 1
% Check for any exact matches (in case any names are subsets of others)
k = strmatch(lowArg,names,'exact');
if length(k) == 1
j = k;
else
msg = sprintf('Ambiguous parameter name ''%s'' ', arg);
msg = [msg '(' Names{j(1),:}];
for k = j(2:length(j))'
msg = [msg ', ' Names{k,:}];
end
msg = sprintf('%s).', msg);
error(msg);
end
end
expectval = 1;
else
[valid, errmsg] = checkfield(Names{j,:}, arg);
if valid
options = setfield(options, Names{j,:}, arg);
else
error(errmsg);
end
expectval = 0;
end
i = i + 1;
end
function [valid, errmsg] = checkfield(field,value)
% CHECKFIELD Check validity of structure field contents.
% [VALID, MSG] = CHECKFIELD('field',V) checks the contents of the specified
% value V to be valid for the field 'field'.
%
valid = 1;
errmsg = '';
if isempty(value)
return
end
isFloat = length(value==1) & isa(value, 'double');
isPositive = isFloat & (value>=0);
isString = isa(value, 'char');
range = [];
requireInt = 0;
switch field
case 'NN'
requireInt = 1;
range=[1 Inf];
case 'GraphNormalize'
requireInt = 1;
range=[0 1];
case 'ClassEdges'
requireInt = 1;
range=[0 1];
case {'Kernel', 'GraphWeights', 'GraphDistanceFunction'}
if ~isString,
valid = 0;
errmsg = sprintf('Invalid value for %s parameter: Must be a string', field);
end
case {'gamma_A', 'gamma_I','GraphWeightParam'}
range = [0 Inf];
case 'KernelParam'
valid = 1;
otherwise
valid = 0;
error('Unknown field name for Options structure.')
end
if ~isempty(range),
if (value<range(1)) | (value>range(2)),
valid = 0;
errmsg = sprintf('Invalid value for %s parameter: Must be scalar in the range [%g..%g]', ...
field, range(1), range(2));
end
end
if requireInt & ((value-round(value))~=0),
valid = 0;
errmsg = sprintf('Invalid value for %s parameter: Must be integer', ...
field);
end
norm2s.m
function [X, Y, normal] =norm2s(x,y) x = double(x); y = double(y); n=size(x,1); m=size(y,1); normal.xm=mean(x); normal.ym=mean(y); x=x-repmat(normal.xm,n,1); y=y-repmat(normal.ym,m,1); normal.xscale=sqrt(sum(sum(x.^2,2))/n); normal.yscale=sqrt(sum(sum(y.^2,2))/m); X=x/normal.xscale; Y=y/normal.yscale;
plot_matches.m
function plot_matches(I1, I2, X, Y, VFCIndex, CorrectIndex)
% PLOT_MATCHES(I1, I2, X, Y, VFCINDEX, CORRECTINDEX)
% only plots the ture positives with blue lines, false positives with red
% lines, and false negatives with green lines. For visibility, it plots at
% most NUMPLOT (Default value is 50) matches proportionately.
%
% Input:
% I1, I2: Tow input images.
%
% X, Y: Coordinates of intrest points in I1, I2 respectively.
%
% VFCIndex: Indexes preserved by VFC.
%
% CorrectIndex: Ground truth indexes.
%
% See also:: VFC(), FastVFC(), SparseVFC().
% Authors: Jiayi Ma (jyma2010@gmail.com)
% Date: 04/17/2012
% Define the maximum number of matches to plot
%blue = true positive+true negative, green = false negative, red = false positive
NumPlot = 50;
TruePos = intersect(VFCIndex, CorrectIndex);%Ture positive
FalsePos = setdiff(VFCIndex, CorrectIndex); %False positive
FalseNeg = setdiff(CorrectIndex, VFCIndex); %False negative
NumPos = length(TruePos)+length(FalsePos)+length(FalseNeg);
if NumPos > NumPlot
t_p = length(TruePos)/NumPos;
n1 = round(t_p*NumPlot);
f_p = length(FalsePos)/NumPos;
n2 = ceil(f_p*NumPlot);
f_n = length(FalseNeg)/NumPos;
n3 = ceil(f_n*NumPlot);
else
n1 = length(TruePos);
n2 = length(FalsePos);
n3 = length(FalseNeg);
end
per = randperm(length(TruePos));
TruePos = TruePos(per(1:n1));
per = randperm(length(FalsePos));
FalsePos = FalsePos(per(1:n2));
per = randperm(length(FalseNeg));
FalseNeg = FalseNeg(per(1:n3));
interval = 20;
WhiteInterval = 255*ones(size(I1,1), interval, 3);
figure;imagesc(cat(2, I1, WhiteInterval, I2)) ;
hold on ;
line([X(FalsePos,1)'; Y(FalsePos,1)'+size(I1,2)+interval], [X(FalsePos,2)' ; Y(FalsePos,2)'],'linewidth', 1, 'color', 'r') ;
line([X(FalseNeg,1)'; Y(FalseNeg,1)'+size(I1,2)+interval], [X(FalseNeg,2)' ; Y(FalseNeg,2)'],'linewidth', 1, 'color', 'g') ;
line([X(TruePos,1)'; Y(TruePos,1)'+size(I1,2)+interval], [X(TruePos,2)' ; Y(TruePos,2)'],'linewidth', 1, 'color', 'b') ;
axis equal ;axis off ;
drawnow;
实验数据:TestData.rar
实验结果
criterion =
0.9259
1.0000
0.9604
0.9615
0.8125