MATLAB粒子群优化算法(PSO)
作者:凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/
一、介绍
- 粒子群优化算法(Particle Swarm Optimization Algorithm)是一种群智能算法,为了寻求全局最优。群体迭代,粒子在解空间追随最优的粒子进行搜索。
- 粒子群算法的思想源于对鸟群捕食行为的研究,模拟鸟集群飞行觅食的行为,鸟之间通过集体的协作使群体达到最优目的,是一种基于Swarm Intelligence的优化方法。
- 马良教授在他的著作《蚁群优化算法》一书的前言中写到:“自然界的蚁群、鸟群、鱼群、羊群、牛群、蜂群等,其实时时刻刻都在给予我们以某种启示,只不过我们常常忽略了大自然对我们的最大恩赐!”
- 设想这样一个场景:一群鸟在随机搜索食物,已知
- (1)在这块区域里只有一块食物; (2)所有的鸟都不知道食物在哪里; (3)但它们能感受到当前的位置离食物还有多远.
- 那么:找到食物的最优策略是什么呢?
- 搜寻目前离食物最近的鸟的周围区域,根据自己飞行的经验判断食物的所在。

- PSO的基础: 信息的社会共享
二、算法思路
- 每个寻优的问题解都被想像成一只鸟,称为“粒子”。所有粒子都在一个D维空间进行搜索。
- 所有的粒子都由一个fitness function 确定适应值以判断目前的位置好坏。
- 每一个粒子必须赋予记忆功能,能记住所搜寻到的最佳位置。
- 每一个粒子还有一个速度以决定飞行的距离和方向。这个速度根据它本身的飞行经验以及同伴的飞行经验进行动态调整。
三、算法流程与伪代码


- c1: weight of local information
- c2: weight of global information
- p: particle's position
- v: path direction
- rand: random variable, 0<rand<1
- number of particles: 10~50
- c1+c2=4
- v=v+c1*rand*(pbest-p)+c2*rand*(gbest-p);中右边第一项v: inertia, c1*rand*(pbest-p): personal influence, c2*rand*(gbest-p): social influence.
四、MATLAB程序
粒子群优化算法求解函数y=x+x*sin(x)在[-10, 10]的最大值.
pso.m
function [best_x, best_y]=pso()
%find the max value of a function
%Author: kailugaji https://www.cnblogs.com/kailugaji/
posMax=10;posMin=-10; %range of feasible solution
x=posMin:0.1:posMax;
y=my_fun(x); %object function
plot(x,y);hold on; %plot function
popsize=30; %number of particles
max_iter=100; %maximum number of iterations
position=rand(popsize,1);
position=position*20-ones(popsize,1)*10; %particle's position
vMax=1;vMin=-1; %range of velocity
velosity=2*rand(popsize,1)-1; %path direction
pbest=position; %current optimum
gbest=position(1); %global optimum
wBegin=1;wEnd=0.05;
c1=2; %weight of local information
c2=2; %weight of global information
for i=1:max_iter
position_new=position+velosity; %change direction of each particle
velosity_new=(wEnd+(wBegin-wEnd)*(100-i)/100).*velosity+c1*rand().*(position-pbest.*ones(popsize,1))+c2*rand().*(position-gbest.*ones(popsize,1)); %inertia+personal influence+social influence
for j=1:popsize
if(position_new(j)>posMax)
position_new(j)=posMax;
end
if(position_new(j)<posMin)
position_new(j)=posMin;
end
if(velosity_new(j)>vMax)
velosity_new(j)=vMax;
end
if(velosity_new(j)<vMin)
velosity_new(j)=vMin;
end
if(my_fun(position_new(j))>my_fun(pbest(j)))
pbest(j)=position_new(j);
end
if(my_fun(position_new(j))>my_fun(gbest))
gbest=position_new(j);
end
end
position=position_new;
velosity=velosity_new;
end
plot(gbest,my_fun(gbest),'or');
best_x=gbest;
best_y=my_fun(gbest);
my_fun.m
function y=my_fun(x) y=x+x.*sin(x);
五、实验结果
>> [best_x, best_y]=pso()
best_x =
8.0051
best_y =
15.9190
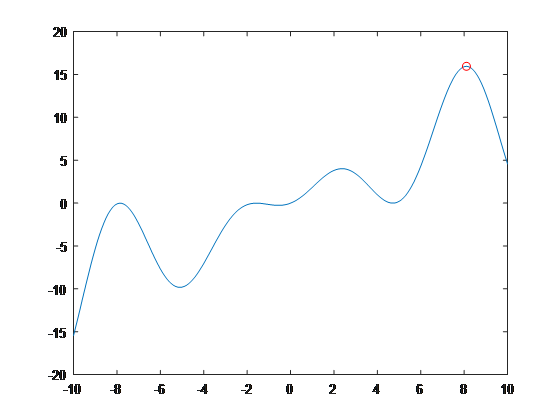
当x=8.0051时,粒子群优化算法终止迭代,此时获得的最大值为y=15.9190。


